Asymmetric dominance and trade proposals

Imagine that you own Kevin Youkilis. You’re a Yankees fan and you hate the Red Sox, so you want to get rid of him out of spite. So you toss him up on the trading block and list outfielders and starting pitchers as your needs. The next morning, one manager offers you one of the following players for Youkilis:

1) Matt Kemp
2) Roy Halladay

Which offer are you more inclined to accept?

It turns out that you’re not sure which you one you want, so you let the trade offers linger for a couple days until the other owner cancels them. A week later, you find that that manager has now offered you a choice of three players for Youk:

1) Matt Kemp
2) Roy Halladay
3) Alex Rios

Now which offer are you more inclined to accept? Did your answer change at all?

The point I am trying to illustrate is one that was raised by one of our readers, Ben, here in the comments section of my previous article. That idea is the asymmetrical dominance effect , also known as the decoy effect.

The asymmetrical dominance effect is the phenomenon in which people show a change in preference between two items when a third item, dominated by either of the first two items, is introduced as an option. There are multiple research studies in which this effect is manifested, and I’ll describe two of them, beginning with the one mentioned in the comments section of the article linked above.

The first study is one that was conducted by Dan Ariely, and in this experiment, students at the University of North Carolina and Duke University were presented with prospective dating partners and instructed to pick a single person to ask out on a date. Three different types of situations were presented:

1). Situation 1 consisted of dating options A and B, both of whom were attractive but had varying degrees of attractive characteristics.
2). Situation 2 consisted of dating options A, B and C(a), with C(a) being almost but not quite as appealing as A.
3). Situation 3 consisted of dating options A, B and C(b), with C(b) being almost but not quite as appealing as B.

So a graphical illustration might look something like this:

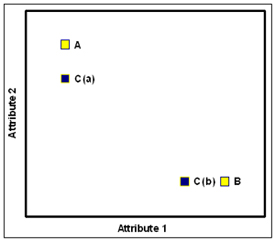
The results of this experiment helped support the asymmetrical dominance effect. Participants were more likely to select dating option A over dating option B when the third dating option, C(a), who was slightly less appealing then A, was present. And conversely, participants were more likely to choose dating option B over dating option A when the third dating option, C(b), who was slightly less appealing than B, was present.

The effect manifests in situations outside of partner selection as well. The second study I want to describe is another study by Ariely. This time, subjects were divided into two groups. In group one, subjects decided between microwaves A and B, with microwave A being expensive and of high quality, and with microwave B being less expensive and of medium quality. Forty percent of the subjects in group one preferred microwave A and 60 percent preferred microwave B.

Subjects in group two had three microwaves to choose from: microwaves A and B, and then a third microwave, C(a), that was very similar in dimensions and quality to microwave A, but was more expensive. So in this scenario, it was very clear that microwave C(a) was dominated by microwave A.

A graphical illustration of this paradigm presented to group 2 might look something like this:

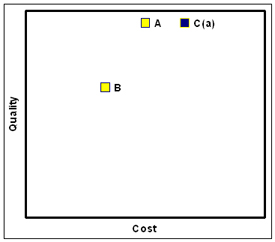
While the majority of subjects in group one preferred microwave B to microwave A, the subjects in group two showed a different preference. This time, 56 percent of subjects chose microwave A, 36 percent chose microwave B and the remaining 8 percent chose microwave C(a). Somehow, this introduction of the third microwave, C(a), completely reversed the ratio of preference between microwaves A and B:

                              Microwaves    A       B      C(a)
                              Group 1      40%     60%      --
                              Group 2      56%     36%      8%

Despite differing situations (people/dates vs. microwaves), the underlying theme in both of these studies is the same. That is, that the presence of a third option, one that has an asymmetric dominance relation with one of the two other alternatives, affects a person’s preference of a given alternative over a second alternative.

Let’s go back to my scenario at the top of the page. The construct, according to the studies mentioned earlier, would be as follows:

1) Player A
2) Player B: similar to A but has different attributes
3) Player C(a): dominated by A, meaning he has similar attributes but is slightly less appealing

Using Chone projections for 2009, and using the average draft positions (ADP) as sort of an anchoring point for market value, we’ll have this:

              ADP     Runs     HR     RBI      BA      SB      W       K      ERA     WHIP
Matt Kemp      38      84      16      74    0.311     26
Roy Halladay   46      --      --      --      --      --      13     152     3.56    1.22
Alex Rios      39      86      17      75    0.285     19

In looking at these stat lines, I think it’s pretty clearly that Alex Rios serves as Matt Kemp’s decoy. They both have similar attributes (R, HR, RBI), but Rios is slightly less appealing (lower BA and less SB). In other words, Rios is dominated by Kemp and would most likely never be chosen in this scenario given these numbers.

As Ben asked a couple weeks ago, the question then, is can this actually be applied to fantasy baseball?

My answer is yes, I do think that the asymmetric dominance effect can manifest itself within the realms of fantasy baseball. If we look at Ariely’s study, each potential dating option had varying degrees of attractive characteristics; some were funnier than others, some more intelligent, others a little more honest, and so on. Each option had different levels of attractive attributes that made it more (or less) appealing than the other options. We do the same thing with baseball players but instead of judging them by cost and quality like we did with the microwaves, we look at runs, home runs, batting average, etc.

Considering that these items are essentially the same, presenting our trade proposals in a similar format as with the dating options and microwaves should have some sort of effect since, what really matters, is the contextual configuration of the options. This doesn’t mean these types of trade proposals will always work, as there are many variables to consider. And, after all, the opposing manager can still decline all three proposals whereas the subjects in these studies were forced to pick. However, it does seem as if designing trade proposals in this way would have an effect in that it may increase the likelihood that a trade will happen in the first place or that the third, lesser player will really serve as a decoy.