Barrels, Normative Analysis, and the Beauties of Statcast

Brandon Moss was one of the unluckiest sluggers in 2015. (via Hayden Schiff)
Introduction
Statcast—MLB’s player-tracking, ball-tracking, everything-tracking tool—has improved in accuracy and volume each year since its inception. The data it provides are uniquely valuable. Thus, we need to ask an important question: How can we put these data to good use?
My purpose in writing this article is to create a set of statistics that measures how well a player should have performed based on Statcast data. I accomplished this with the creation of three new measurements: eSLG, eISO and eHR/G. We’ll go into these terms in-depth later, but for now, it’s important to know what my original intent was.
Each year, it happens that players who performed brilliantly the season before underachieve the next year. Then there’s another set of players who post career-high numbers just a summer after struggling through statistically-depressing seasons. Regression, be it positive or negative, is a staple of major league baseball. So how can we predict which players are most likely to succumb to regression? The answer lies in Statcast. Using Statcast data, I developed expected results for 407 eligible batters from 2015 and 2016. This is where eSLG, eISO and eHR/G come from.
Basic Process
I examined Statcast results for batters with at least 150 batted ball events (balls put in play). I combined sabermetrics and Statcast data in a spreadsheet of 407 hitters from the 2015 and 2016 seasons, then mixed and matched different variables to evaluate positive or negative correlations. I wanted to see which Statcast variables correlated highest with basic and advanced statistics; then, I could start with normative analysis and expected output. I used R to perform linear regressions and other modeling like scatterplots with least-squares lines to show trends. Some of the most interesting discoveries came from Barrels, which was recently unveiled by Major League Baseball.
The New ‘Barrels’ Statistic
MLB’s newest Statcast treasure is called Barrels. It measures a player’s ability to put the barrel of the bat on the ball and generate good contact. Per MLB.com, “A barrel is defined as a well-struck ball where the combination of exit velocity and launch angle generally leads to a minimum .500 batting average and 1.500 slugging percentage.”
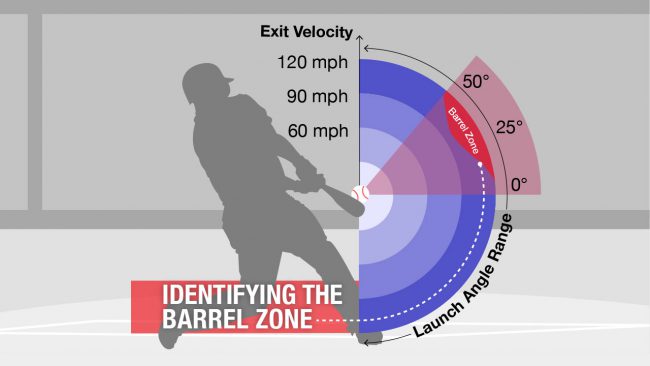
(via MLB.com)
The “barrel zone” is shown in the graphic above; it starts at an exit velocity of 98 mph with a launch angle between 26 and 30 degrees, and then extends outwards.
Mixing and Matching: Statcast and Sabermetrics
As some preliminary research, I ran linear regression analyses on Statcast and advanced analytics variables, as displayed in Table 1 below. Their R-squared values—which show correlation, with a higher value meaning the two variables are more closely associated—are listed.
| Variable 1 (Statcast) | Variable 2 (FanGraphs) | Correlation (R-squared) |
| Barrels/PA | wRC | 0.4034 |
| Barrels/PA | SLG | 0.5900 |
| Barrels/PA | BA | 0.0021 |
| Barrels/PA | wOBA | 0.3970 |
| Barrels/PA | HR/G | 0.7513 |
| Barrels/PA | ISO | 0.7647 |
| Avg Exit Velocity | wRC | 0.3173 |
| Avg Exit Velocity | wOBA | 0.3336 |
| Avg Exit Velocity | SLG | 0.3953 |
| Avg Distance | wRC | 0.2440 |
| Avg Distance | wOBA | 0.2698 |
Barrels: Relationships with Other Statistics
The first thing we can note is that Barrels Per Plate Appearance, known henceforth as B/PA, has high correlations with three statistics: Isolated Power (ISO), Home Runs Per Game (HR/G) and Slugging Percentage (SLG). Graph 1 shows the B/PA-SLG relationship.

Graph 2 shows the B/PA-ISO relationship.

Graph 3 shows the B/PA-HR/G relationship.

Slugging Percentage represents the total number of bases a player records per at-bat. It attempts to correct the flaws that come with Batting Average—that not all hits are created equal. Thus, when calculating SLG, extra weight is given to doubles, triples and home runs. ISO does something similar, but ultimately subtracts batting average from slugging average. For homers, I had to use HR/G rather than HR to account for the fact that players who played more games would dominate the home run projections simply because they had more opportunities. Measuring on a per-game basis averages out the totals and highlights which players hit homers at higher rates.
So why do ISO, SLG and HR/G have stronger positive relationships with Barrels in comparison to other stats? Well, how do those three measurements differ from other statistics like On-Base Percentage (OBP) and Weighted On-Base Average (wOBA), for example? Essentially, ISO, SLG and HR don’t deal with walks and hit-by-pitches—they rely on the ball being hit. Barrels can only occur when the ball is hit in play. Parts of OBP and wOBA—a more advanced stat that estimates the value of each walk, hit or hit-by-pitch and then churns out a value—trust heavily on walks and hit-by-pitches, which clouds the correlations between B/PA and these statistics. (For those who might not fully understand wOBA, it’s helpful to think of SLG as a less sophisticated hits-only version of wOBA.)
It’s only logical that hitting more balls on the barrel of the bat will lead to more hard-hit balls, which will result in more hits, a higher slugging average, and more isolated power and home runs.
Locating Luck
I wanted to see which players in 2015 got “unlucky,” meaning they hit a high percentage of balls on the barrel of the bat and at a good launch angle, but weren’t rewarded with high slugging percentages, high isolated power numbers, or an appropriate amount of home runs. In the next sections, I’ll run through how we can establish who was “lucky” and who was not. Using linear regression models, I found the equation of the least squares regression line for each relationship (and each scatterplot) from above. Using these equations, I then determined what every qualified player should have recorded in 2015 for each statistic being measured. I named this statistic by putting an “e” in front of the y-variable stat. For example, the expected Slugging Percentage (eSLG) for Jon Jay in 2015 was 0.365. His actual slugging percentage (aSLG) was 0.257. I’ll go into more detail for each of the three statistics below.
Finding eSLG
To find expected slugging percentage (eSLG) based on B/PA, I first ran the linear regression analysis, then used R numerical summaries to determine the equation of the least squares regression line. The equation was y = 2.0553X + 0.349.
Plugging in B/PA as the x-variable, I found eSLG for each qualifying player. Finally, I subtracted eSLG from aSLG to demonstrate whether a player slugged above or below what he should have based on how often he put the barrel of the bat on the ball.
As a side note, I believe other analysts have attempted to do something similar with Exit Velocity and even Launch Angle, before Statcast released Barrels. However, Exit Velocity doesn’t correlate nearly as strongly with slugging percentage and other statistics. Thus, I think we can safely use Barrels now that it has been released and is statistically significant.
Here are the “unluckiest” and “luckiest” players of 2015, based on what they should have slugged:
| Player | eSLG | aSLG | SLG +/- |
| Brandon Moss | .522 | .407 | -.115 |
| Giovanny Ushela | .441 | .330 | -.111 |
| Jon Jay | .365 | .257 | -.108 |
| Kevin Plawecki | .398 | .296 | -.102 |
| Chris Carter | .528 | .427 | -.101 |
| Chris Iannetta | .433 | .335 | -.098 |
| Leonys Martin | .402 | .313 | -.089 |
| Michael Bourn | .370 | .282 | -.088 |
| Willson Ramos | .444 | .358 | -.086 |
| Tyler Flowers | .439 | .356 | -.083 |
| Justin Smoak | .550 | .470 | -.080 |
| Yasmani Grandal | .481 | .403 | -.078 |
| Justin Maxwell | .417 | .341 | -.076 |
| Player | eSLG | aSLG | SLG +/- |
| Bryce Harper | .534 | .649 | .115 |
| Francisco Lindor | .400 | .482 | .082 |
| AJ Pollock | .419 | .498 | .079 |
| Joey Votto | .462 | .541 | .079 |
| David Peralta | .448 | .522 | .074 |
| Joe Panik | .388 | .455 | .067 |
| Michael Brantley | .415 | .480 | .065 |
| Nick Hundley | .407 | .467 | .060 |
| Andres Blanco | .444 | .502 | .058 |
| Nolan Arenado | .518 | .575 | .057 |
| Maikel Franco | .441 | .497 | .056 |
| Mark Teixera | .495 | .548 | .053 |
| Dustin Pedroia | .388 | .441 | .053 |
Notice that some of the “luckiest” players are some the game’s best hitters. Bryce Harper had one of the greatest seasons ever in 2015—can we really attibute any of this to luck?
Research has proven that major leaguetalent is, in general, normally distributed, so it would make sense that the players who overperformed or underperformed their expected slugging averages based on Barrels would regress to the mean.
I looked at the slugging percentages of each of these players in 2016, to see if they did in fact regress.
| Player | 2015 eSLG | 2015 aSLG | SLG +/- | 2016 aSLG | Δ 2015 eSLG to 2016 aSLG | SLG Δ 2015 to 2016 |
| Brandon Moss | .522 | .407 | -.115 | .500 | -.022 | +.093 |
| Giovanny Urshela | .441 | .330 | -.111 | N/A | N/A | N/A |
| Jon Jay | .365 | .257 | -.108 | .383 | +.018 | +.126 |
| Kevin Plawecki | .398 | .296 | -.102 | .247 | -.151 | -.049 |
| Chris Carter | .528 | .427 | -.101 | .486 | -.042 | +.059 |
| Chris Iannetta | .433 | .335 | -.098 | .331 | -.102 | -.004 |
| Leonys Martin | .402 | .313 | -.089 | .383 | -.019 | +.070 |
| Michael Bourn | .370 | .282 | -.088 | .372 | +.002 | +.090 |
| Willson Ramos | .444 | .358 | -.086 | .491 | +.047 | +.133 |
| Tyler Flowers | .439 | .356 | -.083 | .410 | -.029 | +.054 |
| Justin Smoak | .550 | .470 | -.080 | .401 | -.149 | -.069 |
| Yasmani Grandal | .481 | .403 | -.078 | .489 | +.008 | +.086 |
| Justin Maxwell | .417 | .341 | -.076 | N/A | N/A | N/A |
| Player | 2015 eSLG | 2015 aSLG | SLG +/- | 2016 aSLG | Δ 2015 eSLG to 2016 aSLG | SLG Δ 2015 to 2016 |
| Bryce Harper | .534 | .649 | .115 | .439 | -.095 | -.210 |
| Francisco Lindor | .400 | .482 | .082 | .436 | +.036 | -.046 |
| AJ Pollock | .419 | .498 | .079 | .390 | -.029 | -.108 |
| Joey Votto | .462 | .541 | .079 | .529 | +.067 | -.012 |
| David Peralta | .448 | .522 | .074 | .433 | -.015 | -.089 |
| Joe Panik | .388 | .455 | .067 | .379 | -.009 | -.076 |
| Michael Brantley | .415 | .480 | .065 | .282 | -.133 | -.198 |
| Nick Hundley | .407 | .467 | .060 | .440 | +.033 | -.027 |
| Andres Blanco | .444 | .502 | .058 | .406 | -.038 | -.096 |
| Nolan Arenado | .518 | .575 | .057 | .573 | +.057 | -.002 |
| Maikel Franco | .441 | .497 | .056 | .417 | -.024 | -.080 |
| Mark Teixera | .495 | .548 | .053 | .343 | -.052 | -.205 |
| Dustin Pedroia | .388 | .441 | .053 | .449 | +.061 | +.008 |
As was expected, most of the players in the tables regressed to the mean, or at least moved a little closer to the average. Of the “unlucky” players, notice that of the players who remained in the majors in 2016, only Plawecki, Iannetta and Smoak didn’t see their slugging percentages rise. And Plawecki has actually played most of 2016 in the minor leagues, where he’s slugged an impressive 0.484.
The “lucky” players mostly showed regression, too. Bryce Harper is the most apparent, but every other player besides Dustin Pedroia also decreased in slugging percentage in 2016. It should be noted AJ Pollock and Michael Brantley are both recovering from injuries, and though their slugging averages have fallen, they’ve each played in just a handful of games.
Finding eISO
Determining Expected Isolated Power (eISO) for a player is similar to how we found eSLG. The equation for eISO was y = 1.982412X + 0.083254. Simply plug in the player’s B/PA percentage and the result will be what his ISO should have been based on how often he hit the ball on the sweet spot of the bat.
Here are the “unluckiest” players of 2015, based on what they should have posted in terms of ISO:
| Player | eISO | aISO | ISO +/- |
| Brandon Moss | .250 | .181 | -.069 |
| Giovanny Ushela | .172 | .105 | -.067 |
| Jorge Soler | .200 | .137 | -.063 |
| JD Martinez | .313 | .253 | -.060 |
| Giancarlo Stanton | .400 | .341 | -.059 |
| Michael Bourn | .103 | .045 | -.058 |
| Anthony Rendon | .157 | .100 | -.057 |
| Jacoby Ellsbury | .143 | .088 | -.055 |
| Kevin Plawecki | .131 | .077 | -.054 |
| Tyler Flowers | .170 | .118 | -.052 |
| Player | eISO | aISO | ISO +/- |
| Mark Teixera | .224 | .293 | .069 |
| Rajai Davis | .121 | .182 | .061 |
| Bryce Harper | .262 | .319 | .057 |
| Jed Lowrie | .129 | .178 | .049 |
| Stephen Drew | .135 | .180 | .045 |
| Maikel Franco | .172 | .217 | .045 |
| Evan Gattis | .174 | .217 | .043 |
| Russell Martin | .176 | .218 | .042 |
| Nolan Arenado | .246 | .287 | .041 |
| Ben Zobrist | .135 | .173 | .038 |
Now let’s do the same thing we did with slugging percentage—that is, take a look at how these players have fared in 2016. Did regression occur with ISO as it did (for the most part) with SLG? Let’s look again at both sides.
| Player | 2015 eISO | 2015 aISO | ISO +/- | 2016 aISO | Δ 2015 eISO to 2016 aISO | ISO Δ 2015 to 2016 |
| Brandon Moss | .250 | .181 | -.069 | .265 | +.015 | +.084 |
| Giovanny Urshela | .172 | .105 | -.067 | .105 | -.067 | .000 |
| Jorge Soler | .200 | .137 | -.063 | .200 | .000 | +.063 |
| JD Martinez | .313 | .253 | -.060 | .230 | -.083 | -.023 |
| Giancarlo Stanton | .400 | .341 | -.059 | .254 | -.156 | -.087 |
| Michael Bourn | .103 | .045 | -.058 | .112 | +.009 | +.067 |
| Anthony Rendon | .157 | .100 | -.057 | .175 | +.018 | +.075 |
| Jacoby Ellsbury | .143 | .088 | -.055 | .114 | -.029 | +.026 |
| Kevin Plawecki | .131 | .077 | -.054 | .063 | -.067 | -.014 |
| Tyler Flowers | .170 | .118 | -.052 | .143 | -.027 | +.025 |
| Player | 2015 eISO | 2015 aISO | ISO +/- | 2016 aISO | Δ 2015 eISO to 2016 aISO | ISO Δ 2015 to 2016 |
| Mark Teixera | .224 | .293 | .069 | .146 | -.178 | -.147 |
| Rajai Davis | .121 | .182 | .061 | .144 | +.023 | -.038 |
| Bryce Harper | .262 | .319 | .057 | .197 | -.065 | -.122 |
| Jed Lowrie | .129 | .178 | .049 | .059 | -.070 | -.119 |
| Stephen Drew | .135 | .180 | .045 | .258 | +.125 | +.078 |
| Maikel Franco | .172 | .217 | .045 | .181 | +.009 | -.036 |
| Evan Gattis | .174 | .217 | .043 | .255 | +.081 | +.038 |
| Russell Martin | .176 | .218 | .042 | .178 | +.002 | -.040 |
| Nolan Arenado | .246 | .287 | .041 | .279 | +.033 | -.008 |
| Ben Zobrist | .135 | .173 | .038 | .159 | +.024 | -.014 |
The results are similar to those we obtained from running the numbers to get Expected Slugging Percentage. Players who overperformed in 2015—those who likely benefitted from luck—saw their ISOs decrease by an average of 0.040 in 2016. Those who underperformed based on their B/PA had their ISOs increase by 0.021 in 2016. So it’s clear that some players just have bad luck some years—they hit the ball on the sweet spot of the bat more often than most, but aren’t rewarded with base hits.
Finding eHR/G
The final statistic we’ll develop is Expected Home Runs Per Game, or eHR/G. Once again, we’re focusing on home runs as one of the three main stats because it holds such a strong correlation with Barrels. The process is pretty much the same as it was for finding eSLG and eISO, so I won’t go into great detail.
The equation for eHR/G was y = 339.348X + 2.1723. We make B/PA percentage the input and eHR/G the output. If a player hit more home runs then he should have based on the percentage of balls he hit on the barrel, we call him “lucky,” at least during the 2015 season. If he hit less homers per game than would be expected, we call him “unlucky.”
Let’s go back to the tables.
| Player | eHR/G | aHR/G | HR/G +/- |
| Justin Smoak | 0.26 | 0.14 | -0.12 |
| Brandon Moss | 0.22 | 0.13 | -0.09 |
| Randal Grichuk | 0.25 | 0.17 | -0.08 |
| Abraham Almonte | 0.14 | 0.06 | -0.07 |
| Brandon Belt | 0.20 | 0.13 | -0.07 |
| Stephen Piscotty | 0.18 | 0.11 | -0.07 |
| Andres Blanco | 0.13 | 0.07 | -0.06 |
| Clint Robinson | 0.14 | 0.08 | -0.06 |
| Jorge Soler | 0.16 | 0.10 | -0.06 |
| Kendrys Morales | 0.20 | 0.14 | -0.06 |
| Player | eHR | aHR | HR +/- |
| Mark Teixera | 0.19 | 0.28 | 0.09 |
| Albert Pujols | 0.18 | 0.25 | 0.07 |
| Dustin Pedroia | 0.07 | 0.13 | 0.06 |
| Carlos Correa | 0.16 | 0.22 | 0.06 |
| Carlos Gonzolez | 0.21 | 0.26 | 0.06 |
| Jed Lowrie | 0.08 | 0.13 | 0.05 |
| Brian McCann | 0.14 | 0.19 | 0.05 |
| Nelson Cruz | 0.24 | 0.29 | 0.05 |
| Nolan Arenado | 0.22 | 0.27 | 0.05 |
| Edwin Encarnacion | 0.22 | 0.27 | 0.05 |
You know the drill—we will now take a look at homer per game rate for the 2016, to see if regression to the mean occurred for the players in both of these tables.
| Player | 2015 eHR/G | 2015 aHR/G | HR/G +/- | 2016 aHR/G | Δ 2015 eHR/G to 2016 aHR/G | HR/G Δ 2015 to 2016 |
| Justin Smoak | 0.26 | 0.14 | -0.12 | 0.11 | -0.15 | -0.03 |
| Brandon Moss | 0.22 | 0.13 | -0.09 | 0.22 | 0.00 | +0.09 |
| Randal Grichuk | 0.25 | 0.17 | -0.08 | 0.18 | -0.07 | +0.01 |
| Abraham Almonte | 0.14 | 0.06 | -0.07 | 0.03 | -0.11 | -0.03 |
| Brandon Belt | 0.20 | 0.13 | -0.07 | 0.11 | -0.09 | -0.02 |
| Stephen Piscotty | 0.18 | 0.11 | -0.07 | 0.15 | -0.03 | +0.04 |
| Andres Blanco | 0.13 | 0.07 | -0.06 | 0.05 | -0.08 | -0.02 |
| Clint Robinson | 0.14 | 0.08 | -0.06 | 0.05 | -0.09 | -0.03 |
| Jorge Soler | 0.16 | 0.10 | -0.06 | 0.14 | -0.02 | +0.04 |
| Kendrys Morales | 0.20 | 0.14 | -0.06 | 0.20 | 0.00 | +0.06 |
| Player | 2015 eHR/G | 2015 aHR/G | HR/G +/- | 2016 aHR/G | Δ 2015 eHR/G to 2016 aHR/G | HR/G Δ 2015 to 2016 |
| Mark Teixera | 0.19 | 0.28 | 0.09 | 0.12 | -0.07 | -0.16 |
| Albert Pujols | 0.18 | 0.25 | 0.07 | 0.21 | +0.03 | -0.04 |
| Dustin Pedroia | 0.07 | 0.13 | 0.06 | 0.10 | +0.03 | -0.03 |
| Carlos Correa | 0.16 | 0.22 | 0.06 | 0.14 | -0.02 | -0.08 |
| Carlos Gonzalez | 0.21 | 0.26 | 0.06 | 0.17 | -0.04 | -0.09 |
| Jed Lowrie | 0.08 | 0.13 | 0.05 | 0.02 | -0.06 | -0.11 |
| Brian McCann | 0.14 | 0.19 | 0.05 | 0.15 | +0.01 | -0.04 |
| Nelson Cruz | 0.24 | 0.29 | 0.05 | 0.28 | +0.04 | -0.01 |
| Nolan Arenado | 0.22 | 0.27 | 0.05 | 0.26 | +0.04 | -0.01 |
| Edwin Encarnacion | 0.22 | 0.27 | 0.05 | 0.27 | +0.05 | 0.00 |
Reviewing the tables above, it looks at though the data aren’t quite as telling for players who supposedly underperformed in home run rate in 2015. But for the overachievers, it’s a whole different story. The average “lucky” player in 2015 saw his HR/G rate fall by 0.06 bombs per contest. That’s almost 10 home runs over the stretch of a 162-game season. Using this model, we probably could have predicted that Mark Teixera, who somehow belted 31 homers while only averaging 0.07 barrels for every plate appearance, would take a big step backwards in power numbers in 2016. Analysis like this can be invaluable to a team deciding which players it wantso go after in the trade market and who it might want to forget about when signing free agents.
Using eSLG, eISO and eHR/G
How can we use the three expected statistics? They shouldn’t be the most decisive factor when a ball club makes choices regarding acquiring players or letting them go. But the concept is similar to Pythagorean Wins, which tell us how many wins a team should have given itsrun differentials. For example, the Texas Rangers have the best record in the AL in 2016, but Pythagorean Wins says they should have 13 fewer wins because they don’t outscore teams by much. This type of normative analysis can be advantageous when evaluating players without bias.
Conclusion
Using my model, we can plug in a player’s Barrels/PA to find what his slugging percentage, isolated power, and home run totals should be. This isn’t always telling—many factors decide the fate of every batted ball—but if the difference between eSLG and aSLG is abnormally large, if eISO is much lower than aISO, if eHR/G is twice as high as aHR/G, regression might be coming up in the near future.
References & Resources
- MLBAM Baseball Savant Statcast Leaderboard
- FanGraphs
- Mike Petriello, MLB.com, “Barreled up: New Statcast metric shows highest-value batted balls”
Any reason you didn’t run these on stats restricted to balls in play? (Or at least using HR/PA, not HR/G?) Seems to me that including walks and strikeouts is mostly just adding to your correlations.
Also, what happens if you standardize the stats to account for the HR rate spike this year?
Thanks for the comment, Frank. You’re right—it would have been better to restrict the Barrels measurement to Barrels/BBE (Barrels per Batted Ball Event) rather than Barrels/PA. However, I ran the calculations and it turns out the correlations between Barrels/BBE and the three response variables (SLG, ISO, HR) still had high positive R-squared values and were statistically significant. For example, the R-squared for B/BBE-ISO was 0.7401, as opposed to 0.7647 for B/PA-ISO.
I’m with Frank, surely AB or BIP would be better denominators for your ratios than G or PA.
Balls on the ground become hits in different ways than those in the air. The effects of BBS and VLA are different, and mixing grounders and flies together will muddy your results. Analyze them separately, then combine at the end.
I use four batted ball bins –
How many in the air go over the fence for homers?
Of those in the air that remain, how many fell in for hits?
How many ground balls made it to an outfielder for a hit?
Of the grounders that remained in the infield, how many became hits?
Billy, you must have the raw barrel data for every hitter. I’d be interested in seeing a list of the leaders, say, the top 10 in barrels/PA. Based on your correlations, these should be the top sluggers, and even if the correlations with more comprehensive hitting metrics like wOBA or wRC+ are not as strong I’d assume all of these leaders are pretty good hitters overall.
OK, I now see those data are in one of the references on your list.
Hi,
Nice article, I like the idea. But I did have a few questions, some of which may have been answered by the time I post:
1) To further the per G or PA or per BIP, why not examine the rate of HR/Barrels? I ask because I doubt there is a lot of variability in this (if you crush a ball into the air, its hard for the defenders to stop it) but I think that could show the effect of luck against hitters (weather, stadiums, etc.), or possibly identify a group of players who may have a skill (swing path, offensive approach, etc.) that allows them to maximize their HR/B rate. Preferably more than a few years would be ideal, but I wonder if it would be predictive from one year to the next.
2) How come you compare the differences of the SLG of 2015 and 2016 to the eSLG of 2015 only? I feel like this is not comparing apples to apples, unless it can be shown that eSLG is a stable “skill/attribute” that does not vary from year to year. I just feel like that is the same as looking at the amount I paid in taxes in 2015 vs. my salary in 2015, then looking at my 2016 taxes vs. 2015 salary, without accounting for the possibility of getting a raise.
3) This just may be me be a stickler, but the “fanning” of the data in the correlation plot would suggest that using an OLS regression line may not provide the best fit. The relation ship is linear, but the distribution of variance expands as a player either increases his HR/G or B/PA, meaning that upper level performance is not being captured as accurately. This slightly occurs also in B/PA-ISO, but to a lesser degree.
Also, Im surprised by the limited range that is considered “Barreled Balls.” Would this be a stat that favors high ball hitters?
It’s interesting to speculate on what makes a hitter lucky. For HR, it might be an unusual proportion hit over relatively short fences, possibly correlated with a strong pull tendency, or maybe just chance. For SLG and ISO, in addition to HR luck, a batter might hit unusual number of GB down the line that go for extra bases. Speed probably also plays a role. A couple of years ago, there was an article here at FG defining a modified ISO in terms of extra bases just by doubles and triples, and showing that was correlated with speed. So I’d guess that fast players tend to be favored in having SLG and ISO values that exceed expectations from barrel contacts.
Generalizing somewhat from what Josh said in his point 2, we would want to know how quickly barrels stabilize. E.g., in one of the references cited by Billy, there was a list of the top ten in barrels per BIP and per PA. It was also noted that if the BIP criterion (200) was reduced to 100, Gary Sanchez became the clear leader. I assume that increases the confidence or the probability that he’s for real–at least, he does not seem to be benefiting as much from luck as some of those listed in the current article. I’d think that contact data would stabilize fairly quickly, but we don’t know yet how quickly.
Thanks for the work. I expect that the results would be more accurate if the batted ball parameters were mapped directly to the expected value of the statistic of interest, say slugging percentage, rather than losing information with the threshold to get to barrels and then regressing to find the relationship with the statistic. In other words, since barrels are not all created equal and non-barrels are not all created equal, why not use a continuous mapping from batted ball parameters directly to the expected value of the statistic. A method that does this is presented at
http://www.hardballtimes.com/the-intrinsic-value-of-a-batted-ball/
and specific examples of the continuous map from batted ball parameters to several statistics are given at
http://www.hardballtimes.com/the-reliability-of-intrinsic-batted-ball-statistics/
I really enjoyed the read. Please correct me if I missed it but there is no park factor applied here : correct?
I saw Arenado appear a few times on the lucky lists and am not shocked given Coors that he failed to meaningfully regress.
There also seemed to be a number of Giants/M’s/Cardinals on the unlucky lists.
Statcast BatCast for tracking bat flips, plz.
You state that “Research has proven that major leaguetalent is, in general, normally distributed.” What research is that? Everything I’ve seen suggests that it is not normally distributed; e.g. far more players are below average than are above average.
Why do you present the coefficient of determination (what you are calling R-squared or correlation, which is incorrect) rather than the actual correlation (R)? We can tell from the graphs that for those variables that the relationship is positive, but we have to assume it because you are using the coefficient of determination.
Cliff, there’s research going both ways when it comes to the distributing of player talent. Bill James said it is not normally distributed, but studies since have differed with this notion. As an example, check out the histogram in the link below.
http://www.sabernomics.com/sabernomics/ops_replacement.png
I used the R-squared coefficient of determination because it is a measure that allows us to determine how certain one can be in making predictions from a certain model/graph. This article revolves around making predictions based on a model or graph. The more certain we are that we can try to make these predictions, the better off we’ll be.
I couldn’t open that link, but it seems to me that by the most comprehensive measures, talent in baseball can’t be normally distributed. Those who make it to the majors are on the extreme right hand tail of a normal curve. If you consider just that tail section, the players within it are clearly not normally distributed, but lie on a power-type distribution, where there is an inverse relationship between talent, production or whatever measure one uses, and number of players. If, e.g., the cutoff were five SD above the mean, there would be far more players between 5-6 SD than players from 6-7 SD, and still fewer from 7-8 SD.
You can certainly see this with WAR distribution, where most players lie between 0-4 WAR, with far fewer at higher values. WAR, of course, is arbitrary in the sense that what is called zero WAR or replacement value is not actually valueless, but is just assigned as a baseline. But that is just because of that cutoff on the population normal curve, which results in a very large number of replacement or near-replacement players who just make that cutoff. A floor, or peak with no left-hand falling off, is built into the process.
Simpler, more traditional stats, e.g., BA or HR, may approach a normal distribution, and perhaps this is what you’re referring to when you say other research supports the existence of such a distribution. But I think these metrics approach normality because they measure only one aspect of a player’s performance. Players are not selected for the majors just because they have a high BA or a lot of power. These and other factors, such as OBP, baserunning and defense, all come into play. Consequently, the pool of players who actually make the majors is fairly diverse with respect to any one of these factors, and may exhibit a fairly normal distribution. Stats that lie somewhat between these simple traditional measures, on the one hand, and WAR, on the other—e.g., wOBA, which measures overall hitting production—also exhibit an in-between distribution, one that shows some similarity to a normal curve, but with a definite bias towards lower values.
Since the ability to barrel up is just one factor, albeit a very important one, perhaps this is normally distributed, too. But I think it’s important to emphasize that what ultimately determines success at the MLB level is a combination of factors, currently best described in terms of WAR, which is not normally distributed.
A lot of the HR overperformers play in really friendly HR parks and vice versa for underperformers. Teixeira is a huge pull hitter which makes the Yankees park fit him really well.
Barrels. Finally a statistic Eric Hosmer can get behind.
many hitting coaches are already teaching launch angle by either using a hit Trax or by marking that 10-30 degree range which is most productive with lines in the batting cage if they can’t afford a hit Trax.
I think that some of these statistics are off. Moss ISO is only 235
No, the statistics are correct. His 2016 ISO at the time the article was written was .265.
R-squared is the coefficient of determination and explains the variance accounted for between the variables. This makes sense to present in this case because you are using regression, as you mentioned previously. However, correlation is r, or the square root of R-squared. Correlation expresses the strength of a relationship between two variables, R-squared does not. Be careful not to use these statistics interchangeably.