Defining the Pitch Sequencing Question, Part Two

There is still a lot to be learned about the effects of pitch sequencing. (via slgckgc)
Welcome to the second installment of my ongoing attempt to make enough sense of pitch sequencing to start asking the right questions about it. In Part One of this series I explored the impact of changing pitch speeds on batter performance. In this article I’ll be looking at the effect of changing locations.
This is yet another “obvious” area for investigation, but one that I think needs to be thoroughly understood if we are to have any hope of tackling more ambitious pitch sequencing analyses. Furthermore, we have some evidence that major league teams are incorporating strategies based on changing locations with the hope of achieving specific effects.
Quick recap of Part One results
Part One found that, after a first-pitch fastball, pitchers were a bit more effective when they decreased speeds on the second pitch (by 5 mph or more) than when they did not. In one of the comments to the article, MGL observed that there are additional context variables to control for. Specifically, he mused that fastball usage is dependent on score and inning, which is unsurprisingly borne out by the numbers, and that these variables also affect batter behavior. As I said from the beginning, this is complicated stuff!
To quickly check the impact that this observed dependency might have on the results, I reran the analysis but limited the samples to the first three innings.
| Linear weights value per 100 of speed decrease (> 5 mph) after first pitch fastball, first 3 innings, bases empty |
|---|
| First pitch outcome | Sample quantity | Runs per 100 pitches |
| S | 5,839 | -0.95 |
| B | 2,301 | -0.82 |
Unfortunately, MGL was also correct that the samples very quickly become small when you start adding these additional controls: this additional constraint brought the sample down to 2,300 pairs of observations after a ball and 5,800 after a strike. But, at least indicatively, the effect holds with this further restriction on game situation.
Classifying pitch location
Getting back to the task at hand, we are moving on from velocity changes to location changes. To compare locations we’ll use a very coarse split of the strike zone plane into five areas:
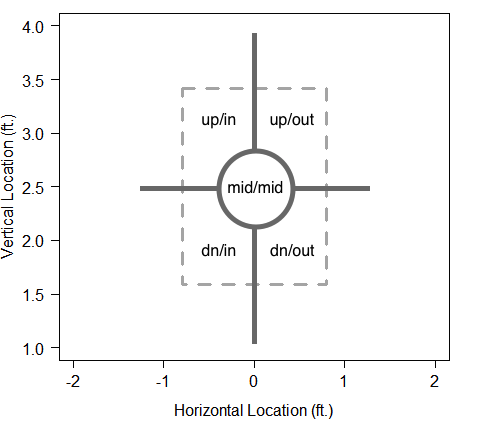
The above graphic is from the catcher’s perspective, assuming a right-handed batter (the in/out labels would be reversed for a left-handed batter). Basically the vertical plane at home plate is divided into quadrants that extend beyond the strike zone, and a circle in the middle (with diameter equal to half the width of the plate) is carved out. Note that the dotted line is a rough indication of the rulebook strike zone, but that my defined regions extend out to infinity.
Typically I see the zones divided into rectangular areas (presumably because the theoretical strike zone is rectangular), but every strike zone “heat map” I’ve ever seen is more circular or ovular in shape. So I’m looking at round shapes to try to match the way umpires and players seem to see pitches. What I’ve done here may not be the best way to divide things. But again, I’m looking for something simple to see what it tells us.
Question Two: What is the impact of changing sides?
As a quick reminder, the comparison method used here is the “delta method.” (See Part One for a full description of this technique.) For this analysis we’re dividing the plate by grouping the two “in” regions together as “inside” and the two “out” regions as “outside”.
| Linear weights value per 100 of second pitch outside after first pitch inside, first 3 innings, bases empty |
|---|
| First pitch outcome | Sample quantity | Runs per 100 pitches |
| S | 1,805 | 0.36 |
| B | 1,480 | -1.29 |
| Linear weights value per 100 of second pitch inside after first pitch outside, first 3 innings, bases empty |
|---|
| First pitch outcome | Sample quantity | Runs per 100 pitches |
| S | 1,857 | 0.36 |
| B | 1,326 | 0.65 |
The samples are small and the deltas are all over the place. Going outside after an inside ball looks like it has been effective, but otherwise changing sides has been less effective than sticking to the same side. The latter is somewhat intuitive: If a given batter has a weakness (or a pitcher has a strength) on one side of the plate or the other, it would make sense that (a) pitchers tend to start by attacking that side, and that (b) attacking the other side of the plate would tend to be worse than going back to the same side.
Question Three: What is the impact of changing levels?
For this analysis, we’re dividing the plate by grouping the two “up” regions as “up” and the two “dn” regions as “down”.
| Linear weights value per 100 of second pitch down after first pitch up, first 3 innings, bases empty |
|---|
| First pitch outcome | Sample quantity | Runs per 100 pitches |
| S | 1,516 | 1.04 |
| B | 1,265 | -0.52 |
| Linear weights value per 100 of second pitch up after first pitch down, first 3 innings, bases empty |
|---|
| First pitch outcome | Sample quantity | Runs per 100 pitches |
| S | 2,472 | -0.32 |
| B | 1,471 | 1.51 |
In both the up-to-down and down-to-up cases, switching levels has been effective after either a ball or a strike, but not both, and not effective enough to offset the ineffectiveness of switching levels in the other case. Again, this is somewhat intuitive. If a batter has a weakness (or a pitcher has a strength) up or down in the zone, it would make sense that continuing to pitch to that level is more effective than switching away from it, assuming that pitchers are starting off by attacking the more desirable location on the first pitch.
Conclusions so far
So, to recap: we’ve looked at changing speeds previously, and today at moving inside to outside, outside to inside, high to low, and low to high. And our results have been… mixed? Then again, maybe it really is true that pitchers should be dropping speeds more often, coming back inside after an outside ball more often but otherwise changing sides less often, and changing levels more in some situations and less in others. If so, great! Let’s go grab a beer while analysts across major league baseball shove spreadsheets in the faces of their teams’ catchers telling them that they’re doing it wrong.
I jest, of course. Your inner MGL should be shouting “Bayes, Bayes, Bayes!” (metaphorically, of course… if you have an actual inner MGL that shouts at you I suggest counseling). If we take the perfectly reasonable prior that pitchers and catchers are doing a pretty good job of mixing up the locations and speeds of the first two pitches of each plate appearance, then we’d probably expect to see that maybe some combinations have negative deltas (outside pitch after an inside ball, low pitch after a high ball, high pitch after a low strike, and don’t forget reducing speed after a first-pitch fastball), others have positive deltas (everything else), and overall the deltas would be about zero. Which is basically what we see: five positive deltas and five negative deltas with a simple average of 0.002 runs per 100 pitches.
Not to mention that, given the small sample sizes, we may be observing in large part the effect of “mistakes”; i.e., a pitcher intends to throw nothing but low fastballs against a given hitter, but sometimes accidentally puts the second higher in the zone and it gets hammered, thus ending up in our sample as a positive delta. Which is not to say that we can’t learn anything from a high fastball just because it was intended to be thrown low. But from a prescriptive standpoint, “make fewer mistakes” is less useful than “have a different intention.”
So in conclusion… there is probably no conclusion to be drawn yet. But it is looking less and less likely that the basic advice of changing levels, sides and speeds presents any untapped potential at the major league level.
Does that mean that we should give up, pack up our databases and go back to doing productive things for society? Of course not! My goal here is to try to understand everything I can about pitch sequencing, working up from the basics, until there are enough building blocks to piece together the questions we should be asking. And even though this analysis has turned up no smoking guns so far, there are still lessons here that point in new directions.
Specifically, I believe they point to digging more deeply into the individuality of player skills. My handful of analyses so far have controlled for batter/pitcher match-ups, but otherwise treated them as interchangeable. The results have been less than satisfying, and there are very obvious reasons to think that the approach is fundamentally wrong: Pitchers have different arsenals, batters have different blends of contact and power, and what works best for pitcher A against batter X may not work for pitcher B against batter Y.
To explore that possibility further, my next article will look at what happens on the very first pitch of a plate appearance for different batter/pitcher match-ups.
Preview: A curious case…
As a little teaser, consider the curious case of Dustin Pedroia and Billy Butler. From 2008-2014, both batted nearly the same number of times (4,478 plate appearances for Pedroia vs. 4,451 for Butler) and achieved identical results, with a wRC+ of 118 for both, according to FanGraphs. Furthermore, they achieved these results with nearly identical walk rates (9.4 percent vs. 9.0 percent), batting averages (.299 vs. .295) and isolated power (.148 vs. .154). And yet Pedroia watched strike one sail by without offering 47 percent of the time, while Butler only did so 35 percent of the time.
So, over the course of a full plate appearance Pedroia and Butler have been almost the same hitter. But the processes by which they have gotten there, and the first-pitch tactics used against them, are different in at least one glaring way.
What does this say about the links among batter skills, pitching tactics and pitch sequencing? My next article will try to shed some (very dim) light on this topic.