Measuring the Change in League Quality (Part 3)
The last two weeks, we have looked at how league quality has evolved over time. We have found that baseball players have improved quite a bit over the past 135 years, though all-time greats like Honus Wagner and Ty Cobb still rank among the best of all-time, regardless of era.
Frankly, after last week’s article, I thought I was done with this particular topic, at least for the time being. But an interesting critique by Nate Silver has led me to re-examine it once more. Bear with me.
Probably the most important adjustment I made in measuring the change in league difficulty from year to year was to account for regression to the mean. The basic concept of regression to the mean is that extreme performances tend to average.
Since players are more likely to be given a lot of playing time if they had a good season the year prior, regression to the mean tells us that on average, players will get worse from year-to-year. Think about it this way: If you have two “true talent” .270 hitters, but one hits .240 and the other hits .300, the next season, the .300 hitter will be starting while the .240 hitter will be lucky to stay on the 25-man roster. Both will hit .270 that next year, but because the .300 hitter will have received so many more plate appearances, combined, the two will appear to have gotten worse, which would suggest that the league they’re playing in has gotten better.
So we have to adjust for regression to the mean to avoid those kinds of issues. But we have to be careful; if we over-adjust, our results will end up too flat. Wrote Nate: “In short, I’m quite certain that David is regressing to the mean too much, and throwing the baby out with the bathwater.”
I believe Nate may be right, for two reasons. The first is that when I examined how much to regress to the mean, I found that we needed to add about 445 plate appearances of league average performance to a player’s batting line. Later, looking in The Book, I found that the authors suggested using 400 plate appearances. In practice, the difference isn’t all that great, but I decided to tune down my regression accordingly.
The second issue is a bit more involved, and it necessitates understanding just what regression to the mean is. See, though we generally just regress a player’s statistics to the major league average, that’s actually a bit of a shortcut.
Let’s say I played a game in the major leagues because I had some unflattering pictures of Terry Francona. Of course, I would go 0-for-4, but what would happen if you tried to project my statistics for next season? Well, if you regressed to the major league mean, you would find that I was projected to be just about average because the small sample size means that my numbers are going to be regressed almost 100%.
But of course, that’s preposterous! No one would actually believe that I should be projected as a major league average player. The mistake we’re making in our projection is regressing me to the major league average. What we would want to do is regress my statistics to the average of all college students who were never good enough to play even high school baseball. And of course, the average college student who wasn’t good enough to play high school ball would hit just about .000 in the major leagues.
So why is that important to us in trying to answer this specific question about league difficulty? Well, what if we’re incorrectly handling regression to the mean? Let’s say that the quality of competition is getting better at a higher rate than we found, which is what Nate is arguing. That would mean that we are understating the year-to-year decline in players’ statistics.
Could we be doing that? Well, let’s say you have a good player who puts up a .340 wOBA one season. We regress that to .330. Now let’s say that because the league became a lot more difficult, he only puts up a wOBA of .300 the next season, and we regress that to .310. In that case, we would be understating the rise in league quality by 50%! Indeed, our regression method could be giving us incorrect results!
So what do we do? Taking an idea from an article Nate wrote a couple of years ago, I think I have a solution.
We can find the relationship between a player’s performance and the amount of playing time he gets over his career; the better he is, generally, the more he’ll play. So what I did was grouped players into 16 different categories based on their career plate appearances (discounting seasons in which they pitched), and found the wOBA of each category. Predictably, as plate appearances went up, so did the wOBA.
Specifically, the pattern was logarithmic, and I came up with the following equation to predict wOBA from a player’s career plate appearances:
0.018515*ln(PA) + 0.165
The correlation between actual and predicted was .99.
So what next? Well, instead of regressing each player’s wOBA to the overall average, I regressed it to his predicted wOBA based on career plate appearances. Hank Aaron’s seasons, for example, were regressed to a .342 wOBA, rather than .316. This way, we avoided over-regressing a player’s statistics, and understating the change in league quality.
So what was the result? Here is a graph comparing the old method with the new:
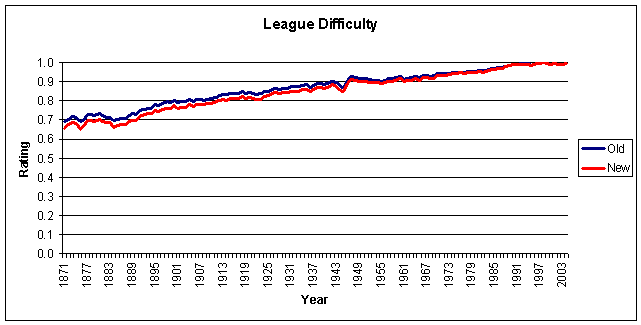
(Note: I am still only using 26- to 29-year-old players, as detailed in last week’s column.)
Despite the changes, the actual difference is minimal! Over the past forty years, the results match pretty much exactly, and before that, the new method tracks the old, but shows a slightly lower level of league difficulty. Nonetheless, let’s re-do the numbers for all individual leagues as well:

(Note: Click on picture for a larger version.)
So using these new, though barely changed numbers, let’s address Nate’s specific criticisms (I’ve left out one because Nate made a mistake in reading the graph in my last article; these results only go through 2004). Nate compared my method’s conclusions to those made by Clay Davenport’s method, which I critiqued in part one. Needless to say, Nate thought Clay’s method was closer to the truth:
So why did Nate conclude that my method was understating the changes in league quality? I believe there’s an issue of scale here. For example, my league difficulty rating for the 2004 American League is .997, while it’s .993 for the National League. So basically no difference, right? Over a full season, that means an average player in the American League was 2.4 runs better than an average player in the National League. That’s not a huge difference, but it certainly isn’t nothing.
Heck, in 1971, I find that the average player in the National League was 16.3 runs better than the average player in the American League, but that’s a difference of just 2.7% in league difficulty. In other words, those little differences are a lot bigger than they look on the graph.
So what’s the conclusion? Nate was right: I did have to tune down the regression to the mean. But, it turns that didn’t make a big difference, and well, the change in league difficulty is what we thought it was.
References & Resources
Click here for an addendum to this article.
