Money and wins

Okay, we all know that teams with bigger payrolls tend to win more games. We know it so well, in fact, that many people consider it the scourge of baseball, the evil lurking in our fanatical hearts, the dark side of the force out. Call it the Alpha Team theory of major league ball. If you’re a fan of an Alpha Team, life is good. If you’re a Pirates fan, well, you’ll always have Willie Stargell and Rennie Stennett.

I’m not out to debunk the Alpha Team theory; far from it. I would just like to give it some historical perspective. This is possible thanks to some terrific data collection by THT co-founder Matthew Namee. Matthew recently compiled the payrolls of all major league teams from 1976 through 2011, the Free Agent Years. Matthew has been using the data to analyze the effectiveness of general managers, which is a really cool idea. Consider this article a background piece to his more detailed analyses.

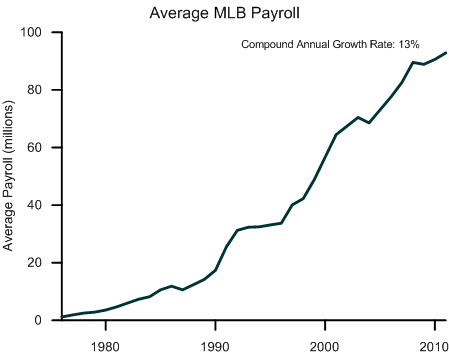
Let’s start at the very beginning. In 1976, the average team payroll was about $1 million; in 2011, it was $93 million. That’s a 13 percent compound growth rate over 35 years. During the same time period, inflation has grown 4.5 percent a year. The S&P 500 index has grown 7.6 percent a year. If you could have invested in baseball players in 1976, you’d be buying lots of THT Forecast subscriptions right now.

Plus, there were just 24 teams in 1976; now there are 30. More teams. More payroll. A boatload of money is now paid to major league ballplayers. It wasn’t always thus.

If you were around at the time, you remember 1976. The month before the New Year, December, 1975, was the month that Peter Seitz changed the economics of baseball by declaring Andy Messersmith and Dave McNally free agents. This ruling basically undermined the reserve clause. Chaos ensued. The owners postponed spring training in 1976, though Bowie Kuhn finally forced them to open their gates. The Twins traded Bert Blyleven. Charlie Finley sold his best talent, though Kuhn overruled that, too. 24 players refused to sign contracts during the 1976 season and were declared free agents at the end of the year. Reggie Jackson, Joe Rudi, and Bobby Grich were among the players who subsequently signed multi-year deals for over a million dollars each. Mike Schmidt didn’t go the free agent route, but the Phillies signed him to the richest contract (at the time) in baseball history ($3.4 million for four years) just to cover themselves.

And on and on. Bottom line: the average team payroll leaped nearly 90 percent from 1976 to 1977.

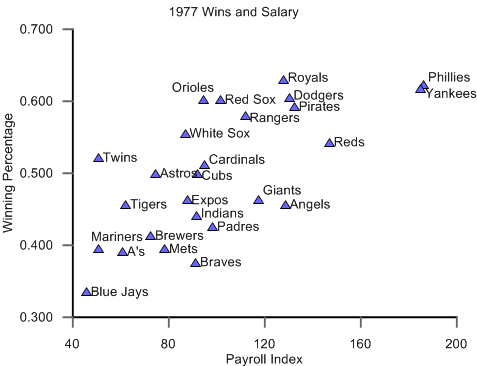
And wins followed suit. The relationship between payroll and team performance had already been strong—in 1976, the correlation (otherwise known as “R”) between payroll and winning percentage was 0.55—but that correlation jumped to 0.7 in 1977.

The graph on the right shows how much each team spent and won in 1977. It’s pretty easy to draw a line through the data points, isn’t it?

The Phillies, with their veteran lineup featuring Schmidt, Greg Luzinski and Steve Carlton, won 101 games but lost the NL Championship series to the Dodgers. The Yankees, who had been wandering the desert without a world championship for over a decade, took it all with Jackson, Don Gullett and Catfish Hunter leading the payroll. It seemed as though money truly was becoming destiny.

Okay, enough with the ancient history. Let’s step back, take in the big picture and ask: how have payroll and wins correlated since the free agency explosion? Has the relationship between the two stayed as strong? The answer is, “it’s complicated.”

Below is a graph of the year-by-year correlation (R, not R-squared) between the payroll and wins. A high R means that wins closely followed payroll; a low R means that results on the field were more random than payroll would imply. Take a note of the ups and downs during these years.

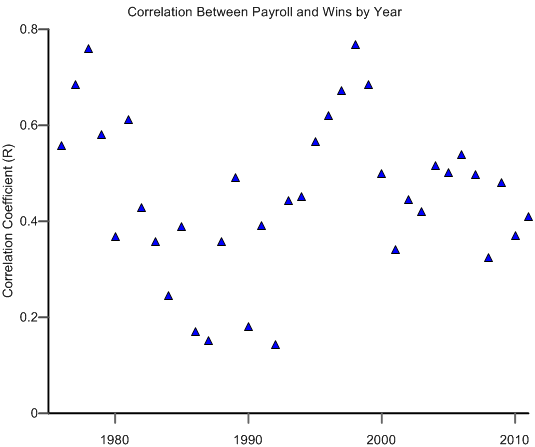
As you can see, there have been two periods in which money and performance were closely tied: the last half of the 1970s and the last half of the 1990s. The last half of the 1980s, however, was a period of relative equal measure, when both rich and “poor” teams had relatively even chances of winning. Some historical review is in order (the following are my thoughts. Be sure to leave your own observations below).

In the first few years of free agency—the latter half of the 1970s—teams did take advantage of new opportunities by signing top talent to big bucks. It’s no coincidence that this period coincided with the Steinbrenner Yankees’ return to glory and the introduction of two bottom-dwelling, low-pay expansion teams (the Mariners and Blue Jays). These developments exacerbated the differences between the have’s and have-not’s.

Beginning around 1980, however, the picture changed as young, lower-paid talent began to make an impact on the pennant races. Players such as Eddie Murray and Cal Ripken in Baltimore, Rickey Henderson in Oakland and George Brett in Kansas City changed their team’s fortunes before changing their payrolls. The Mets developed a gaggle of phenomenal, “cheap” young talent. This influx of top young talent helped change the picture in the early part of the decade. At the same time, bad contracts started appearing. The Angels became the first team known for its bloated, underperforming contracts.

Something else happened in the 1980s: collusion. In 1985, 1986 and 1987, free agents such as Andre Dawson, Tim Raines, Jack Morris and many others found no market for their services. It turns out that commissioner Peter Ueberroth had convinced major league owners that they should work together to refuse expensive, long-term contracts. The owners reportedly established standards of no more than three years for position players and two years for pitchers. As a result, average payroll actually declined in 1987.

The impact on the the economics of winning was stark, and the correlation between wins and payroll reached two of their lowest points in 1986 and 1987 (0.17 and 0.15, respectively). Money was losing its power and competitive balance seemed possible. Trouble was, this was illegal. In three different cases, arbitrators ruled that the owners had colluded and eventually ordered them to pay damages.

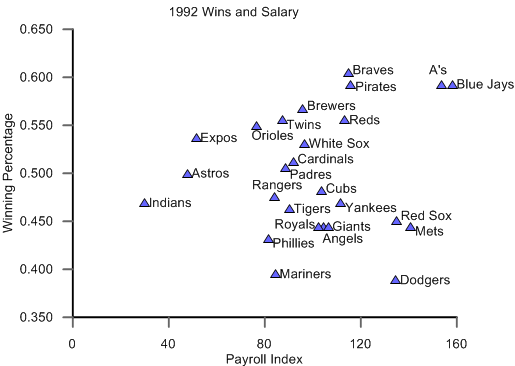
1992 was the nadir of money’s influence, when wins and payroll had a correlation of just 0.14. On the left, the graph for 1992 looks like a random scatterplot. The Dodgers, notably, won only 63 games despite paying Daryl Strawberry over $4 million. And I don’t mean to pick on Strawberry. The Dodgers paid a lot of guys a lot of money. Obviously, this was a team effort in economic futility—one of the ten worst in our database.

In 1993, the Rockies and Marlins joined the National League and the era of relative economic equality ended in the major leagues. After the labor strife of 1994 and 1995, high-spending teams started winning strong once again. By 1998, the correlation between salary and wins was 0.77, the highest correlation in the history of our little bit of data. The Yankees and Braves were at the top of the charts, the Expos and Marlins at the bottom, and the Alpha Team worriers seemed to have reason to worry once again.

In fact, a 2000 “blue ribbon panel” (where did that term come from, anyway?) recommended that Major League Baseball institute a system of revenue sharing, essentially taxing the rich teams and giving to the poor ones. Then, in 2001 and 2002, Moneyball was played in Oakland and Billy Beane’s A’s mounted two of the three best win/salary performances of all the teams and years in our database. (Said differently, the A’s won many more games than their payrolls would have predicted, based on the overall major league patterns.)

Certainly we can argue whether teams really did learn how to better spend their payroll dollars. What’s less arguable is that the commissioner did indeed start to share revenue between teams according to payroll, and a formal revenue-sharing scheme was codified in the 2006 Collective Bargaining Agreement.

Has this worked? Go back up to the graph and take a look. For the past decade, the average correlation between wins and salary has settled into a “natural” space between 0.3 and 0.5. There are still big payrolls, to be sure, and those teams are more likely to win games. But we haven’t seen the extreme correlations between payroll and wins that we witnessed in the past.

For a little more insight, here’s one last graph. It’s called a “box-whisker” graph because it shows boxes and, um, whiskers around the median payroll each year. In this case, I’ve calculated the 2011 equivalent of each team’s salary and plotted each year on the graph. The boxes above and below the median represent the first two quartiles; that is, half the teams fall within those two boxes. The whiskers show the outside 25th percentile, but I’ve put an arbitrary limit on those outer quartiles so you can spot the outliers. Those are the triangles that fall outside the whiskers.

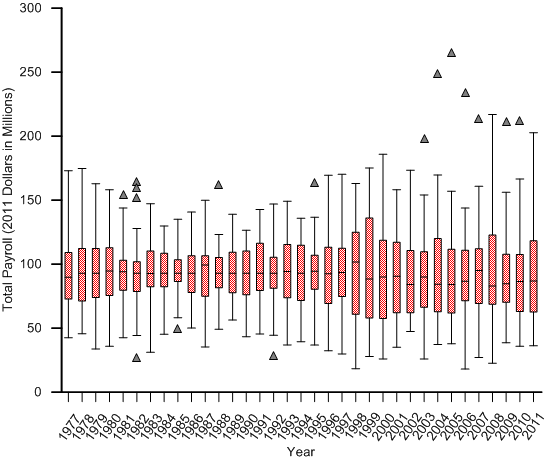
See all those outlier triangles starting around 2000 and lasting all decade? Those are the Yankees. Even in the years in which the Yanks don’t technically break out as outliers, they stretch the lines to their fullest height. On a inflation-adjusted basis, the Yankees of the 2000’s have nine of the top ten spending teams of all time. The only team to break up that run is the Yankees of 1999. So, it’s all Yankees.

Check out the other trends. See how narrow the quartiles were in the collusion years? Notice that, indeed, teams became more spread out in the late 1990s. When the Yankees fall into outlier territory in the 2000s, the quartiles look about as wide as previous years. If you graph the Yankees as outliers, the spread between teams in the 2000’s is roughly the same as it was in the 1970’s and late 1990’s, perhaps a bit larger.

So here’s the point: Wins and salaries are closely tied, but the relationship between the two has changed over time. There is no doubt that some of the change has been random, or the simple result of individual team successes and failures, but some of it also seems to be related to structural changes in the game. The current state of the game? Despite the outrageous spending ways of the Yankees, it’s settled into a pattern that is more competitive than any previous time period, other than the years of collusion.

One other point: We’re measuring payroll against regular-season wins here, so the extra randomness added by expanding the playoffs to include wildcard teams isn’t accounted for. This is another factor that has given “poor” teams a reason for hope.

So, hey Pittsburgh fans, maybe there is some hope. Hang in there.

References & Resources
You can find payroll information at Baseball Chronology.

It’s a little dated, but this is a nice history of baseball economics.

This is a research article on the impact of revenue sharing in the 2000’s.