Optimizing the Swing

Finding the optimal swing path is the goal of every hitter. (via Minda Haas)
When I first started writing this article a few weeks ago, the focus was very simple. It was motivated when someone posted a link to a 2004 Wall Street Journal article, “Why Hitting Curveballs Scores More Runs; How Pedro Proves Rule,” in which it was claimed that an optimally hit curveball can be hit farther than an optimally hit fastball.
The article was based on an interview with Professor Mont Hubbard of UC Davis, who earlier had published an article in the American Journal of Physics, “How to hit home runs: Optimum baseball bat swing parameters for maximum range trajectories,” which directly addressed this topic. Some discussion ensued on Twitter, concluding with a question posed to me: Is the claim fact, theory, or nonsense?
The essential idea behind the claim is quite easy to state. On the one hand, a faster pitch can be hit harder and, therefore, can travel farther than a slower pitch. That would seem to give the edge to a fastball over a curveball. On the other hand, a curveball can be hit with greater backspin than a fastball. Greater backspin means more lift, which leads to a longer distance on a fly ball.
In the WSJ article, Hubbard goes through a very nice explanation for why a curveball can be hit with greater backspin than a fastball. It is the ultimate in simplicity and worth repeating here. If the ball approaches the batter with topspin then reverses direction, the topspin becomes backspin. That is, a curveball with topspin is already spinning in the right direction for the batted ball to have backspin. But a fastball with backspin has to reverse its spin direction for the batted ball to have backspin. So, for two otherwise identical pitches, the one with topspin will be hit with more backspin than one with backspin. That, in a nutshell, is the qualitative argument.
So we have two competing effects. On the one hand, we have the higher exit speed of the fastball. On the other hand, we have the higher rate of backspin on the curveball. The ultimate question is, which one “wins”? Based on a detailed calculation by Hubbard et al. (hereafter denoted by SHS, the first letter of the names of the three authors), the curveball wins. To state the result more precisely, SHS determined that an optimally hit curveball can be hit farther than an optimally hit fastball. The claim is based on real science and definitely is not nonsense. And it definitely is theory, in the sense that it is based on a calculation. Is it fact? I will address that shortly.
In the process of going back and re-reading the SHS article, I decided to redo all of their calculations using the most up-to-date physics models for the ball-bat collision and for the flight of a baseball. What started out as a simple article has turned into a real research project, with an emphasis not only on the fastball/curveball issue but more generally on optimizing the batter’s swing. So, with that lengthy introduction, here we go.
To set the stage for the analysis to follow, let me first show you a simplified diagram of the geometry of the ball-bat collision. This is a side view at the moment of initial contact. The ball moves downward from right to left along the blue arrow at the “descent angle” relative to the horizontal. The bat moves upward from left to right along the red arrow at the “attack angle”.
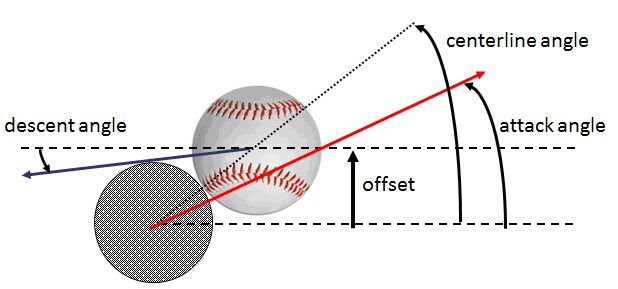
Also shown on the diagram are the “centerline angle” and the “offset.” The centerline is the dotted line connecting the center of the bat to the center of the ball, and the centerline angle is the angle the centerline makes with the horizontal. The offset is the vertical distance between the centers of the ball and bat. Those two things are related. (For those who like a little math, the sine of the center line angle is the ratio of offset to the sum of ball and bat radii, about 2.7 inches).
Armed with this diagram, let’s talk about the forces the bat exerts on the ball that cause it to change both its direction and its spin. First is the “normal” force, which acts directly along the center line, pointing up and to the right in the diagram. It is the primary force that changes the direction of the ball. Second is the frictional force, which occurs whenever there is relative motion between the ball and bat along their mutual surfaces (i.e., perpendicular to the center line). Friction contributes both to a change in direction and to a change in the spin rate.
As an example of these forces in action, take a look at the GIF below, which comes from an experiment I did a few years ago. A baseball is fired without spin from a cannon at 120 mph, impacts a fixed cylinder made of ash, then bounces, all the while viewed by a high-speed video camera at 2,000 frames/second. This collision is very much like the one in the above diagram, with the ball direction horizontal and zero bat velocity. The ball strikes above the center of the cylinder then bounces off the cylinder up and to the right with a considerable amount of backspin.

A still image captured from the video is shown in the next picture, with the ball in contact with the cylinder. The dotted white arrow shows the direction of the normal force, which is along the centerline. A component of the initial velocity is along the surface of the bat, perpendicular to the centerline and pointing up and to the left. During the collision, the ball slides in that direction, resulting in a frictional force acting in the opposite direction, as indicated by dotted yellow arrow. The friction contributes to the change of direction of the ball and causes the ball to rotate counterclockwise (i.e., with backspin). If the ball had impacted below the center of the cylinder, the friction would have been in the opposite direction, so that the ball would have bounced down and to the right with a clockwise spin (i.e., with topspin).

In general, there are two independent parameters under the batter’s control that characterize the swing, which I will seek to optimize in the calculations. First is the offset, which is a measure of the batter’s aim and determines the center line angle. The second is the attack angle. The interplay among the attack angle, the descent angle, and the center line play important roles in the fate of the batted ball, as we will see in the following simple example.
Suppose a ball is hit off a tee, so that there is zero pitch speed and spin. Suppose further that the offset and attack angle are adjusted by the batter so that the attack angle of the bat is right along the center line. Under such conditions, there is no sliding and, therefore, no friction, and the ball will exit along the center line with zero spin. If the attack angle falls below the center line, the friction will be down and to the right on the diagram, so that the ball will exit the bat with backspin and in a direction below the center line. Similarly, if the attack angle falls above the center line, the ball will exit with topspin and above the center line.
These observations are all qualitative. To find quantitative results requires a detailed model for the ball-bat collision. The model used by SHS was largely untested experimentally at the time of his publication. Since then, newer experiments have been done leading to an improved understanding of the ball-bat collision and a better model, particularly as relates to the spin of a batted ball. Similarly the aerodynamic model used herein also is improved based on experiments performed subsequent to the SHS work.
Before going to the calculations, I want to emphasize that I have made several simplifying assumptions in my model for the swing. SHS made the same assumptions. I have assumed the bat is perfectly horizontal and perpendicular to the line connecting home plate to second base at the time of collision. In PITCHf/x language, the pitch is moving along the y axis, and the bat is oriented parallel to the x axis so that the batted ball goes to straightaway CF. Clearly, this assumption ignores the timing issue, so that the batter is neither out in front nor behind on the pitch. It would be straightforward to relax these assumptions in future studies.
Now let’s move on to the calculations. As shown in Table 1, a generic wood bat typical of that used in the major leagues was used along with two different pitch pitches, a fastball with 2000 rpm backspin and curveball with 2000 rpm topspin. The speed and descent angle were based on typical major league pitches from the PITCHf/x database. Also investigated was the situation where a ball was hit off a tee. A fixed bat speed of 70 mph was assumed in all cases. Contact was assumed to occur at the front edge of home plate and three feet off the ground.

| Pitch type | Speed at home plate (mph) | Descent angle (deg) | Spin rate (rpm) |
| Fastball | 85.8 | 6 | 2000 backspin |
| Curveball | 70.7 | 10 | 2000 topspin |
The first question I asked was the one asked by SHS in their investigation: What are the swing parameters that give the maximum batted-ball distance? The results of the optimization process are shown in the contour plots and summarized in Table 2. The plot shows contours of equal distance in the space of attack angle and offset, for fastball and curveball separately. These results may surprise you; they certainly surprised me and forced me to think carefully about why they turned out the way they did. I will now explain.


| Pitch type | offset (in) | centerline angle (deg) | attack angle (deg) | exit speed (mph) | launch angle (deg) | spin (rpm) | distance (ft) |
| Fastball | 1.09 | 23.6 | 18.8 | 100.6 | 29.6 | 2421 | 408.4 |
| Curveball | 1.03 | 22.3 | 17.8 | 100.4 | 30.3 | 2285 | 406.2 |
| Tee | 1.60 | 36.1 | 25.0 | 88.4 | 33.3 | 1212 | 338.7 |
The first surprising result is that the exit speed for fastball and curveball are essentially identical. How is that possible since, all other things equal, I would have expected about a three mph greater exit speed for the fastball? The reason has to do with the so-called Coefficient of Restitution (COR), which is a measure of the bounciness of the ball, and how it depends on speed. In fact, the COR is larger at the lower impact speed of the curveball than at the fastball speed. That fact alone accounts for most of the additional three mph. The rest is buried in even more obscure details of the collision that I won’t bore you with.
The second surprising result is that the backspin on the fastball is actually a little bit larger than that on the curveball despite the qualitative argument given earlier that the backspin on the curveball should be larger. How is that possible? The key to understanding this result is to realize that because of smaller descent angle (see Table 1), the incoming ball moves along a direction further from the centerline for the fastball than for the curveball. As a result, there is a greater sliding speed for the fastball, so that friction acts over a longer period of time, resulting in a much greater change in the spin. In fact, for both the fastball and curveball, the outgoing spin depends far more on things related to how the ball and bat directions are aligned with the center line than it does on the spin of the pitch. The collision model that leads to that result comes from experimental work done subsequent to the SHS article.
When you put it all together, the eye-catching result of SHS that an optimally hit curveball travels farther than an optimally hit fastball is not confirmed by my own analysis. In fact, the fastball beats the curveball, but only by a little bit. My takeaway from this analysis is that the distances are comparable.
One additional thing easily can be seen from the contour plots: If your goal is to hit the ball as far as possible, swinging down on the ball—i.e., with a negative attack angle—does not appear to be a good idea.
Next take a look at the result for hitting off a tee in Table 2. If one attempts to hit the ball as far as possible, it requires an attack angle and an offset that are significantly larger than are optimum for hitting a pitch. I mention this as a cautionary tale that swinging the bat to maximize the distance off a tee can lead to bad habits.
There is undoubtedly much more to be gleaned from this analysis, particularly the contour plots. Rather than do that, however, I want to turn to a slightly different topic. Note from Table 2 that the optimum attack angle is about 18 degrees, which is significantly greater than the descent angle of 6 degrees for a fastball. While such a swing might optimize the batted-ball distance, it is not too forgiving if the swing is mis-timed.
This result suggests that another way to optimize the swing is for the attack angle to be essentially identical to the descent angle, so that good contact still can result even if the timing is a little off. Coaches often refer to that as a “level swing,” although in this context level means the upward plane of the swing coincides with the downward plane of the ball. So I took a look at the process by which the two planes coincide, and the results are summarized in the color contour plot, assuming a fastball.
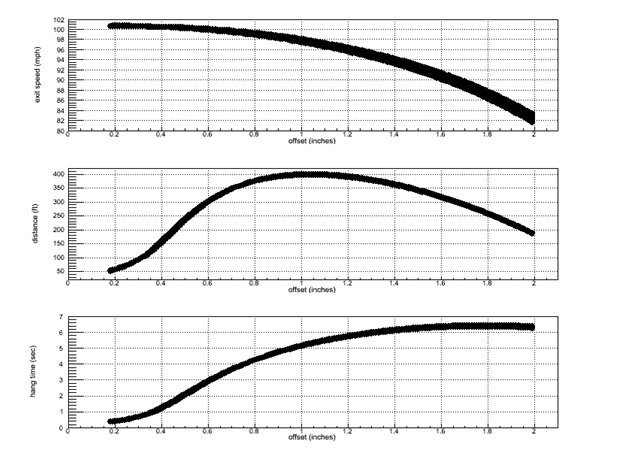
The top plot shows exit speed versus offset and demonstrates that a high exit speed can be achieved with a wide range of offsets. The middle plot shows that maximum distance is achieved with an offset around one inch. That would be the hitting strategy if the goal is to hit a home run. The bottom plot shows that short hang time (along with high exit speed) is achieved with offsets less than 0.5 inch. In effect, this type of hit is a hard-hit line drive with a low launch angle, leading to a safe hit with high probability. These plots demonstrate quantitatively what most people already realize. Namely, that the two different goals (home runs versus on base) require two different hitting strategies.
Let me return to the question that was posed to me: Is the claim that a curveball can be hit farther than a fastball fact, theory, or nonsense? As already mentioned, it is not nonsense, and it is theory. But it is not fact. Moreover, while I very much like qualitative arguments, since they often help us see through the details to get at the essential results, there are times when the details really do matter. This is one of those times.

Your work is some of this biochemist/baseball junkie’s favorite stuff. Great read.
This was really informative and interesting. Awesome work, Professor!
So excited to see this come up this morning! Excellent work, Doc.
For my own curiosity I’d like to know the mass of the bat, although I’m guessing 31 ounces?
Also, in the fastball/curveball distance contours figure it appears the maximum distance for a 6 degree attack angle is in the 390 range. In the three “level swing tables” the max distance appears to be around 410. Is it possible the optimal distance parameters were used to create the last three tables, rather than a 6 degree swing?
On the point of pitch and swing plane matching… Is it possible to estimate the timing advantage of an on-plane swing, ignoring actual online swing adjustments by the hitter? In other words, if we assume the swing is rotating around a fixed axis to produce a 6 degree swing or an 18 degree swing, how many degrees of timing error will each swing tolerate before the ball either misses the sweet spot or the bat altogether? That’s obviously a question for a different study, but it seems possible you might already know the answer so I thought I’d ask.
Again, fantastic work here. Instant classic.
The bat was 34″ long, 31.5 oz in weight. I’m afraid I don’t understand the rest of your question. There are only two tables. Table 2 shows the optimum results (maximum distance), allowing both the attack angle and offset to vary. The last figure assumes fastball only and attack angle=descent angle=6 deg. You can see that the maximum distance under those conditions is a little less than in Table 2. Your last point about timing is definitely a good one and something that ought to be studied. It would be a very straightforward extension of the analysis I have already done. When I find some time…..
Lovely work as usual! “… the two different goals (home runs versus on base) require two different hitting strategies.” Perhaps KC’s success is due to a more base hit oriented hitting strategy as opposed to the home run/strike out strategy that seems too common in the game today. With any luck, other teams and their players will move toward the base hit strategy.
KC simply played 1980’s baseball, its not as if what they did is unusual or novel in any way, its simply that MLB and most of its teams simply do not have this mental approach to the game anymore.
Average Team Differential: Hitting Components Gained/Lost
Year Hits 2B 3B HR XBH 1B CO + E
1980v2010 49 -39 13 -35 -61 110 377
1981v2011 -5 -47 8 -48 -87 82 374
1982v2012 46 -32 6 -35 -61 107 411
1983v2013 37 -25 14 -28 -40 77 358
1984v2014 51 -32 10 -14 -37 88 359
1985v2015 11 -28 6 -25 -47 58 381
w/o 81-11 194 -157 48 -137 -246 440 1886
Team Average Gain/Loss by Category, 1980s teams versus 2010s teams
Year PA SO EXTRA PA W CO + E H SUM HEWCO
1980v2010 14 -366 381 -45 377 49 381
1981v2011 -22 -381 359 -10 374 -5 359
1982v2012 56 -398 454 -2 411 46 454
1983v2013 14 -388 403 8 357 37 403
1984v2014 44 -383 426 16 359 51 426
1985v2015 45 -385 429 37 382 11 429
w/o 81-11 173 -1920 2093 13 1886 194 2093
Average Team Runs and RBI Gained/Lost
Year Runs RBI
1980v2010 -16 -25
1981v2011 -46 -53
1982v2012 -4 -12
1983v2013 24 14
1984v2014 31 20
1985v2015 12 4
w/o 81-11 47 1
In all the charts above, I made the stats equivalent. There were 26 teams in the 80s as compared to 30 now. 1981 was a strike year in which only 2/3 rds of the games were played so not a comparable year, hence “w/o 1981” sum. A positive number in the tables above is the 1980s kicking the butt out of the modern game. A negative number is where the 2010s team’s game excel versus the 1980s teams.
Remember these are PER TEAM AVERAGES. So in 83-85 the average team in MLB score 67 runs more than teams from 2013-15. So 67 * 26 team is a differential of 1742 more runs scored in the 80s for those 3 years, even though the modern game has more doubles, HRs, and by extension slugging. The reason? The 1980s featured more HITS overall, more contact, more contact outs, and more singles. Thats right, the unsexy single and unheralded contact out won more games.
Great article! Thanks
Great work as always, Alan.
There seems to be an interesting theme running through the work you’ve been doing on batted balls: although the various factors affecting batted ball flight are extremely complicated, a lot of them seem to offset each other. In your experiment at Minute Maid Park you found that higher backspin increases lift but also increases drag such that backspin makes little difference in practice; and here you found that higher pitch velocity is offset by lower COR such that exit velocity is similar for the different pitch types. I’m not sure what that means in terms of prescriptive advice for hitters, but it is definitely noteworthy (to me).
That brings me to my one question: in your Minute Maid research you found higher backspin to be an insignificant factor in batted ball distance, but here you accept the premise that higher backspin will indeed cause the ball to travel farther. Was there some additional research after your Minute Maid experiment that found a different result?
Regarding the COR of a baseball: The rules specify a range which is quite large (about 10% variation from top to bottom). That large a range corresponds to a huge difference in exit speed, leading to perhaps a 30 ft variation in distance on a typical long fly ball. I think that most baseballs used in MLB games fall in a very narrow band of COR near the top of the allowed range.
The COR is measured at 60 mph. However, as discussed in the article, there is a significant speed dependence. Based on laboratory data, the COR decrease roughly linearly from about 0.58 at 60 mph (the top of the allowed range) to 0.47 at 150 mph.
The MMP experiment found that there was no significant increase of distance with spin, at least between 2000 and 3200 rpm. The extra lift from a higher spin seemed to be cancelled by a higher drag. But that experiment was done with a very narrow range of exit speeds and launch angles. Before I draw strong conclusions about spin-dependent drag, I would want to explore a broader range. I did not include spin-dependent drag in the calculations for this article.
“…although in this context level means the upward plane of the swing coincides with the downward plane of the bat.”
Typo? “…downward plane of the ball,” right?
Yes, a type. Another typo: Just before the last set of plots, I refer to “color contour plot”. That should simply be “plots”. An earlier draft had color contour plots instead, but I changed at the last minute.
I’m mesmerized by that slo-mo of the baseball striking the bat, and how much it compresses upon impact.
Which leads me to a question. Do baseballs vary a lot in terms of COR? I’ve read your analyses on how much of a batted ball’s trajectory depends upon the ball itself, and from this article it sounds like the COR is a significant factor.
Regarding the COR of a baseball: The rules specify a range which is quite large (about 10% variation from top to bottom). That large a range corresponds to a huge difference in exit speed, leading to perhaps a 30 ft variation in distance on a typical long fly ball. I think that most baseballs used in MLB games fall in a very narrow band of COR near the top of the allowed range.
The COR is measured at 60 mph. However, as discussed in the article, there is a significant speed dependence. Based on laboratory data, the COR decrease roughly linearly from about 0.58 at 60 mph (the top of the allowed range) to 0.47 at 150 mph.
Fascinating results Alan. Do you have a video of a ball bat collision with identical parameters of the one in your post but with pitch backspin instead of no spin? If so I’d love to see if and how the collisions differ. Thanks for sharing your work with us.
Thanks, Peter. I did a whole series of experiments a few years ago with backspin, topspin, and no spin. I have high-speed video for all of them. I see if I can dig up some representative samples and post them on my web site. I tweet out a link when it is ready.
Interesting info. Wood bats and today’s BBCOR bats are smooth and somewhat “slick” from a friction viewpoint. Would small (golfball size or microscopic size) dimples or nubs on the barrel have any positive impacts on backspin or ball exit speed? Also, would a rougher, more gripping surface on the barrel have any positive impacts? Thanks
Interesting question, SJ. The experiment that I did was in collaboration with Rawlings. My interest was studying wood bats. Their interest was studying exactly the point you raised. Namely, is it possible to get higher spin on the batted ball by appropriately roughening the surface. The quick answer is NO, at least for the kinds of surface normally found on bats. If a rubber-like material were used on the surface of the bat, it is likely one could obtain higher spins, as the ball can more easily “grip” the surface. The strings of a tennis racket serve a similar purpose, which is the reason some types of strings are not allowed.
Would be interesting to change the incoming angle and spin based on a submariner. Or how about underhand fastpitch, the ball may be rising and have topspin?