Pitch Arsenal Scores

Adam Wainwright had the second-best arsenal ERA in baseball last season. (via Dirk Hansen)
How do we evaluate a pitcher’s arsenal? In December 2014, Eno Sarris and Daniel Schwartz published a pair of articles in which they constructed and refined a measure of a player’s pitch arsenal score. The concept is a fascinating one; such a metric would enable ready comparison of each pitcher’s “stuff.” We could begin to answer questions such as, which pitch is more valuable, Tyson Ross’s slider (23.0 percent swinging strike rate), or Masahiro Tanaka’s splitter (27.4 percent swinging strike rate)? Perhaps of greater value still, the metric could be used to help identify potential breakout pitchers (i.e., someone who had good peripherals but either suffered from bad luck or simply hadn’t yet figured out how to mix his pitches up effectively).
The comparison of Ross’s slider to Tanaka’s splitter highlights the difficulty of evaluating and ranking each pitcher’s arsenal score. Based on the numbers above, Tanaka’s splitter would seem to be the superior pitch (higher swinging strike rate). Additionally, Tanaka’s splitter induces a higher groundball rate (67.0 percent) than does Ross’ slider (53.1 percent), and ground balls are known to produce the lowest wOBA of any batted ball type. However, Ross threw his slider 41.3 percent of the time, while Tanaka threw his splitter just 24.1 percent of the time. Many would argue that Ross should receive more credit for throwing a pitch so frequently and maintaining such high success with it.
Moreover, the average swinging strike rate on splitters in 2014 was 20.6 percent, with a standard deviation of 20.4, while the average swinging strike rate on sliders in 2014 was 14.4 percent, with a standard deviation of 5.1. Hence, Ross’ swinging strike rate on his slider was 1.69 standard deviations above the mean slider swinging strike rate in the league, while Tanaka’s swinging strike rate on his splitter was just 0.33 standard deviations above the mean splitter swinging strike rate in the league. How, then, do we determine which pitch provided more value?
The difficulties compound further when we move beyond comparing individual pitches and instead compare pitchers’ arsenals in the aggregate. In addition to his devastating splitter, Tanaka features a four-seam fastball, a sinker, a slider, and the occasional cutter and curveball. Ross, meanwhile, augments his elite slider with a four-seam fastball, a sinker, and the rare change-up. How can we compare these two arsenals to one another?
To gain traction on these questions, I collected data on each pitcher’s arsenal. Specifically, I recorded the swinging strike rate, groundball rate, zone percentage rate, and pitch usage for each pitch type for each pitcher. Then, I used this information to explain variation in a pitcher’s ERA using Ordinary Least Squares (OLS) regression analysis (for background on OLS regression modeling, read here and here). Last, based on the estimates from the model, I predicted what each pitcher’s ERA should have been based solely on his pitch type peripherals. The resulting number — which can be interpreted very much like other ERA estimators such as FIP and SIERA — provides a single numerical representation of the quality of a pitcher’s arsenal (like ERA, low numbers are better).
This approach requires a number of assumptions. First, OLS assumes a linear relationship between the explanatory variables (pitch peripherals) and the outcome variable (ERA) — for example, a one unit increase in swinging strike rate will have the same effect on ERA regardless of whether the increase is from five percent to six percent or from 11 percent to 12 percent. The linearity assumption is not always benign. For example, when looking at fastball velocity, some have suggested a pitcher simply needs to clear some basic threshold (e.g., 90 mph) to have an acceptable fastball. If this is true, then fastball velocity would not have a linear correlation with ERA. However, when analyzing the data considered here, the assumption of linearity seems reasonable, even if imperfect.
The second required assumption relates to dealing with missing data. I score each pitcher on each of the nine pitch types thrown by at least 10 pitchers in 2014: four-seam fastball, two-seam fastball, sinker, splitter, cutter, change-up, curveball, slider, and knuckle curve (sorry, no knuckleball or screwball in this analysis). In order to compare all pitchers on an even footing, I had to figure out a way to compare pitchers who had a different pitch mix — for example, as noted above, Ross does not throw a splitter at all, while it is arguably Tanaka’s signature pitch.
In the results that follow, I have assumed a pitcher gets a value of zero on his swinging strike rate, groundball rate, and zone percentage rate for a particular pitch if he does not throw that pitch. So, for example, Ross is assumed to have a zero percent swinging strike rate and groundball rate on his splitter.
This might seem a bit odd, but it can be justified by the following logic: if a pitcher never throws a splitter, it seems safe to assume that he does not know how to throw that pitch in a way that is at all useful to him. Therefore, if he were to suddenly try to throw a splitter in a game, that pitch likely would perform terribly — certainly, we would expect very low swinging strike rates and groundball rates with the pitch. Setting the values of pitch types not thrown equal to zero means that the final estimate of a pitcher’s skill will account not only for the pitches he does throw, but also those that he does not.
One last set of assumptions is imposed by the structural form of the explanatory variables used in the regression model. Each pitcher’s ERA is modeled as a function of 36 variables — four for each of the nine included pitch types. The first variable is an indicator of whether the given pitcher throws that pitch type at least three percent of the time. The second is the pitch’s swinging strike rate multiplied by its usage rate. The third is the pitch’s groundball rate multiplied by its usage rate, and the fourth is its zone percentage multiplied by its usage rate.
By incorporating usage rates into the measure of each pitch peripheral’s success, the model can account for the fact that Ross throws his slider over 40 percent of the time, while Tanaka’s splitter is used at a less frequent rate. It stands to reason that an elite pitch thrown often is of more use to a pitcher than an equally elite pitch thrown infrequently.
The beauty of this technique is that it allows the data to dictate how important each component of a pitcher’s arsenal is in explaining his overall performance (measured here as ERA). Having a high swinging strike rate on a particular pitch type is valuable to a pitcher only insofar as that swinging strike rate is negatively correlated with ERA. For example, swinging strike rate on four-seam fastballs is very strongly correlated with ERA (coefficient of -37.7, p<0.001), while swinging strike rate on sliders is correlated with ERA at a slightly lower magnitude (coefficient of -27.4, p=0.001), and swinging strike rate on curveballs is only weakly correlated with ERA (coefficient of -14.5, p=0.154). This indicates that while a high swinging strike rate on any of these three pitches leads to a lower ERA, it is more useful to have an elite four-seam fastball than it is to have an elite slider or curveball, all else equal.
Similarly, the model supports the intuition that swinging strike rate has a stronger effect on ERA than does groundball rate. Indeed, only the change-up and knuckle curve (the latter was a relatively uncommon pitch type in 2014) have larger negative coefficients on their groundball rates than on their swinging strike rates. While groundball rates are generally negatively correlated with ERA, all other pitches primarily derive their value from high swinging strike rates.
The final note I will add is that I have filtered the analysis to include just the 2014 season and only pitchers who threw at least 100 innings (trying to remove relief pitchers from the analysis for the first cut). With all these caveats in mind, let’s see the arsenal scores!
| Pitch Arsenal Score Leaders, 2014 |
|---|
| Rank | Pitcher | IP | ERA | aERA |
| 1 | Clayton Kershaw | 198.1 | 1.77 | 1.76 |
| 2 | Adam Wainwright | 227.0 | 2.38 | 2.27 |
| 3 | David Price | 248.1 | 3.26 | 2.35 |
| 4 | Chris Sale | 174.0 | 2.17 | 2.41 |
| 5 | Tyson Ross | 195.2 | 2.81 | 2.77 |
| 6 | Masahiro Tanaka | 136.1 | 2.77 | 2.79 |
| 7 | Jeff Samardzija | 219.2 | 2.99 | 2.80 |
| 8 | Felix Hernandez | 236.0 | 2.14 | 2.90 |
| 9 | Jon Lester | 219.2 | 2.46 | 2.91 |
| 10 | Lance Lynn | 203.2 | 2.74 | 2.93 |
| 11 | Stephen Strasburg | 215.0 | 3.14 | 2.97 |
| 12 | Michael Wacha | 107.0 | 3.20 | 2.99 |
| 13 | Francisco Liriano | 162.1 | 3.38 | 2.99 |
| 14 | Max Scherzer | 220.1 | 3.15 | 3.00 |
| 15 | Phil Hughes | 209.2 | 3.52 | 3.01 |
The above table shows the arsenal score (denoted aERA — “a” for “arsenal”) for each pitcher in the data set, along with his 2014 innings pitched and ERA. There are a total of 149 pitchers in 2014 who pitched at least 100 innings. The table is sorted by aERA, with the best at the top.
It is comforting to see largely the usual suspects at the top of the list — Clayton Kershaw stands alone (as he ought to), while Adam Wainwright, David Price and Chris Sale form a distinct second tier with aERAs between 2.27 and 2.41. Things start to get a little more interesting after that, with the aforementioned Ross and Tanaka ranking fifth and sixth, and other slightly lower-profile pitchers such as Lance Lynn, Francisco Liriano and Phil Hughes ranking in the top 15.
Lynn and Liriano placing so highly makes sense, since this measure is based primarily on swinging strike percentage and groundball rate but does not heavily account for walk rate (zone percentage is a bad predictor of walk rate), and we know that Lynn and Liriano shine with strikeouts but struggle with walks. Somewhat more noteworthy is Hughes, who is well known for his absurdly low walk rate but generally is not considered either a strikeout pitcher nor a groundball pitcher. His success in this metric is explained by his four-seam fastball: he posted a swinging strike rate of 9.7 percent, which is 1.82 standard deviations above the league average of 6.0 percent, and he capitalized on the success of his four-seamer by throwing it 61.9 percent of the time.
To get a better sense of the distribution of the data as a whole, here is a plot with aERA on the x-axis and ERA on the y-axis:
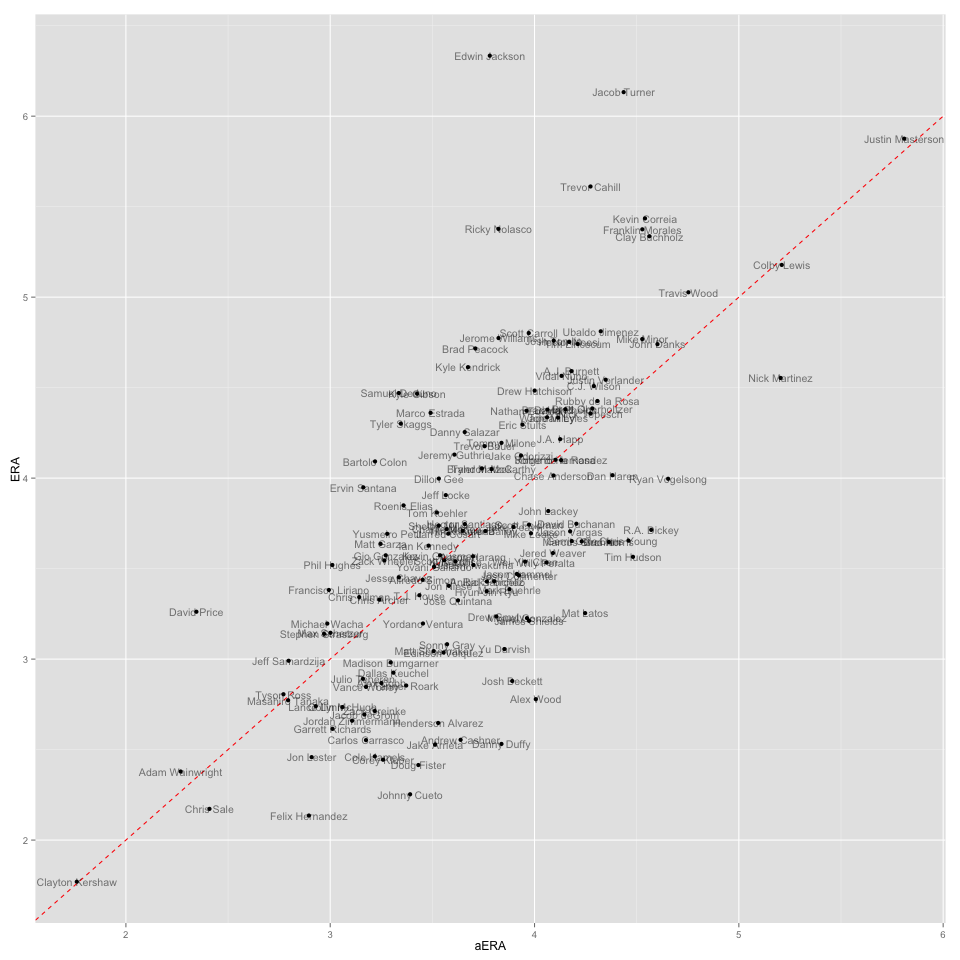
All players above the dotted red line outperformed their ERA, while those beneath the line posted a better ERA than their pitch peripherals would suggest they merited. Unsurprisingly, pitchers such as Henderson Alvarez and Jered Weaver posted significantly better ERAs than aERAs, while the aforementioned Price and Hughes registered impressive aERAs relative to their actual ERAs.
Circling back around to the opening question, we can use the estimated model to answer the question of whether Ross’s slider or Tanaka’s splitter is the superior pitch. First, we multiply each component of Ross’s slider (swinging strike rate, groundball rate, zone percentage, usage) by its weight from the model, then we add the four components together. Ross’s slider receives a score of -1.33, which can be roughly interpreted to mean that Ross’s ERA was 1.33 units lower than it would have been had he never used a slider, ceteris paribus. A similar calculation reveals that Tanaka’s splitter comes in at -0.88. Based on this model, then, we would have to conclude that Ross’ slider was the more valuable pitch.
This measure is far from perfect. Particularly if we want to look at this as an ERA estimator, we know that several values (such as walk rate and infield flyball rate) are not accounted for. That said, it provides an interesting way to incorporate the increasingly granular data available on pitchers into estimators of their performance. Moreover, it opens the door for a much deeper understanding of pitching. As we learn which skills are most strongly connected with pitcher success, we can begin to more thoroughly isolate the role of pitch mixing and identify which sets of pitch types complement one another. A great deal of insightful work has been done on this topic already, but far more awaits.
An analysis of aERA would be incomplete without discussing its predictive power in comparison to other ERA estimators (FIP, xFIP, and SIERA). How can individual pitch type peripherals improve upon our measures of pitcher quality? What is missing from aERA, and how can these gaps best be addressed? I will turn to these questions in my next post.

If you added a linear regression line for the average of the values it would add more credence to the aERA as a measuring tool, at least in comparison to the 1:1 aERA vs. ERA line.
Good comment, Dylan. I decided to go with the 45 degree line for its ease of interpretability, but I agree that fitting a linear regression line would shed more light on who was under- and over-performing their ERA.
This is a great follow up to the fangraphs atricles. It didn’t make sense to me at the time that Kershaw would be 20th, given that he is a true generational talent, so this appears to make a lot more sense intuitively. It does appear to favour guys like Price, Colon and Hughes who use a lot of fastballs, all of whom had much higher ERAs than their estimated aERA.