Redefining Batted Balls to Predict BABIP

Yasiel Puig’s penchant for line drives have him and opponents looking up (via Epic Memories by Ron).
Today, I will release metrics that will help supplement our understanding of hitter batted-ball tendencies and provide a model to predict a hitter’s Batting Average on Balls in Play, or BABIP.
The main tool we use to supplement our understanding of BABIP is batted-ball data. Further on, we will discuss how batted-ball data is currently a poor tool–yet a wildly popular one–to use when speaking in terms of BABIP.
The fact of the matter is, batted balls don’t tell you much about BABIP in the first place, and today I am here to change that with new innovative metrics. We want our measures of batted-ball tendency to actually be predictive and descriptive of BABIP itself. With these metrics and a few other simple components, I believe we can predict BABIP at a high rate, simply using batted-ball data.
Because BABIP can have a large effect on a hitter’s overall performance and value at the plate, we are very interested in finding the magic number/ratio/formula–something that will limit the year-to-year variation in BABIP that currently exists–for all parties involved.
xBABIP is considered the best BABIP estimator, capable of predicting 25 percent of the yearly variation in BABIP using a myriad of different components and complicated adjustments. Today, I will achieve a 23 percent year-to-year variation using only four, with no adjustments, making it a more widely adaptable and useful predictive tool.
Note: All data are from the 2002-2013 sample with 300 plate appearance cutoff, unless otherwise specified.
Background of BABIP and its components
First created as a measurement to evaluate a pitcher’s performance, BABIP is now a well-known statistic that is applied to both batters and pitchers, often used to measure the “luck” in a player’s performance in a given season.
While BABIP has descriptive power, it hardly has any predictive value as its year-to-year correlation for hitters sits at 30 percent (with no PA cutoff) and 35 percent (with a typically popular 300-PA cutoff). The rest is in the hands of random variation and regression to skill-set. This means BABIP in year one can only account for around 12 percent of the change in BABIP in year two, which is not good.
The difference between a hitter’s and pitcher’s BABIP is a matter of control. A pitcher is thought to have little control over his batted ball performance, hence DIPS theory (Defense Independent Pitching Statistics) and the inclusion of strikeouts, walks, and home-runs as the main components of evaluating pitchers. Meanwhile, a hitter is thought to have much more control (relatively speaking) over his BABIP and its components, such as BIP distribution (LD%, FB%, GB%).
So what’s the use of a statistic that has little predictive value? Why do we continue to stick with BABIP as a metric if we know it’s likely to tell us nothing?
BABIP tells us what happened. A high BABIP likely means greater production in all offensive facets of the game like wOBA, BA, oWAR and much more. With knowledge of its fickle nature, we have trained ourselves to simply look at a player’s BABIP and question a player’s ability to maintain a level of performance by making assumptions on whether they will regress or recover.
I’m all for metaphors and imagery, so lets think of BABIP as a “measuring stick” with a big “WHY?” scribbled on the side. Now we can use our measuring stick with great accuracy for analyzing the current season, but forget about using our measuring stick to predict performance when next season rolls around.
If I give you the LD%, FB%, GB%, and BABIP for each batted-ball type, you will have descriptive measurements. But as individual components, they mean very little to BABIP as a whole, in a predictive and descriptive sense.
Using just batted-ball data, you will have a hard time predicting next year’s measurement, let alone the one in progress. Herein lies the problem with how we currently view BABIP and its components. That is why I am introducing supplemental BABIP metrics that are more predictive in orientation.
Dangerous Assumptions
It’s a well-known fact that line drives land for a base hit around 70 percent of the time, followed by ground balls around 20 percent and fly balls landing around 12 percent yearly. However, what we may forget is that these numbers fluctuate wildly season to season. This is the reason why simply looking at LD%, FB%, or GB% will tell you very little about how a player should perform.
There is a whole lot of yearly variation in the subsets of BABIP itself, meaning that BABIP is more reliable than its standalone components, as follows. Numbers below are correlation (r-values) of each metric against BABIP in the current season (BABIP_Y1), in the following season (BABIP_Y2), and the year-to-year correlation (Y2Y):
| Correlations with BABIP, 2002-2013 (min. 300 PA) | |||
|---|---|---|---|
| Metric | BABIP_Y1 | BABIP_Y2 | Y2Y |
| BABIP_LD | 0.37 | 0.02 | 0.12 |
| BABIP_FB | 0.51 | 0.22 | 0.36 |
| BABIP_GB | 0.58 | 0.17 | 0.28 |
| BABIP | 1.00 | 0.35 | 0.35 |
| Correlations with BABIP, 2002-2013 (min. 300 PA) | |||
|---|---|---|---|
| Metric | BABIP_Y1 | BABIP_Y2 | Y2Y |
| LD% | 0.38 | 0.16 | 0.28 |
| FB% | -0.36 | -0.27 | 0.76 |
| GB% | 0.20 | 0.21 | 0.77 |
What these tables show us is that batted ball rates (LD%, GB%, FB%) are relatively stable year to year but do little to describe a hitter’s BABIP in the current or future seasons, yet we commonly use them to supplement BABIP, assuming one must effect the other.
Sure, batted ball rates have stability–in year-to-year correlation–but they consistently don’t tell us much. BABIP components (BABIP_LD, BABIP_FB, BABIP_GB) have more description and around the same level of prediction as batted-ball rates, but they also have the inconsistencies of BABIP itself. The matter of the fact is, batted balls don’t tell you much about BABIP in the first place.
For this reason, you can’t assume that just because a player has an abnormally high LD% one season, he is due to regress dramatically the next. Even if LD% is inconsistent year-to-year and is likely to change in some way, BABIP is not guaranteed to follow along with it. This is because BABIP regression depends on the regression of both how often he hits line-drives and how often those line-drives fall for a hit.
So hitter batted-ball tendencies are a little more nuanced than we perceive them to be. Truly understanding hitter’s batted-ball tendencies as they relate to BABIP will require more legwork than just looking at batted-ball percentages or BABIP on each batted-ball type.
Simply put, not all batted balls are created equal, so we need to compare BABIP to a player’s batted-ball distribution in order to get a better look at how hitter’s BABIP works. We want our measures of batted-ball tendency to actually relate to BABIP.
Measuring hitter tendencies as it relates to BABIP — bMETRICS
Consider this: instead of using the rate at which a batted ball was hit, we are more interested in the probability of a batted-ball type given a hit was recorded (in probability notation: P(Batted Ball Type|Hit). For context, BABIP is a fancy cousin of batting average; BABIP is the probability of a hit given the ball was in play, or simply P(Hit|Ball In Play). We want to talk in the language of hits first, then batted balls.
Note: “|” signifies conditional probability.
Because batted ball rates do not capture the rate at which those balls landed for a hit, I thought that a ratio between the P(Hit|Batted Ball Type) / P(Batted Ball Type|Hit) could give us a more predictive and descriptive view of a hitter’s BABIP. For instance, the ratio of P(Hit|LD) to the P(LD|Hit) would better capture the batted ball as it relates to a player’s ability to get a hit on one.
To calculate the said ratio, we first need the P(Batted Ball Type| Hit)–or what we will call bMETRIC–meaning the percentage of line drives given a hit, ground balls given a hit and then a fly balls given a hit. This is found by using the following formula (below is the example of calculating bLD , which is percentage of hits coming from line drives):
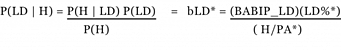
*Note: P(LD | H) = bLD, P(H | LD) = BABIP on line-drives excluding HR’s, P(H) = H/PA excluding HR’s, and P(LD) = LD/PA excluding HR.
Repeat this process for the other two batted-ball types (FB and GB), and we get the line of bMETRICS (bLD, bFB, bGB), which measure the ball-in-play distribution of hits.
Hey, if none of that math made sense to you, think of the bMETRICS as a simple percentage of LDs, FBs, and GBs that fell for hits.
Finding Fly Ball Tendency as it Relates to BABIP — rMETRICS
To get a better measure of hitter tendency, we will take the ratio of BABIP and bMETRICS, which we will name “rMETRICS.”
Our conclusion is that you need to incorporate both BABIP on a certain batted-ball type and the percentage of the player’s hits that were from the given batted-ball type for a more meaningful metric. It’s this ratio that we will call the rMETRIC series.
For example, rMETRIC for LD will follow the following formula:
rLD = BABIP_LD/bLD
rFB and rGB will be found by substituting the “LD” with the proper batted ball. So rFB will equal BABIP_FB/bFB, and so on.
In 2012, Omar Vizquel had a LD% of 34 percent, which is abnormally high. You would expect Vizquel to have a large BABIP overall since he had a skewed number of line drives, which are more likely to land for a hit. However, his rLD (a.k.a BABIP_LD/bLD) sat at 0.8, the second lowest of the entire sample.
The rate at which his line drives were falling for a hit (BABIP_LD) was at a lesser rate of his hits that were line drives (bLD). So a Omar Vizquel line drive is not only worth less than a Yasiel Puig line drive, Vizquel is hitting them at a ineffective rate*. This low rLD may have caused Vizquel’s 0.261 BABIP, something that comes as a surprise considering so many of his BIPs were the most valuable type.
*Note: Puig had a rLD of 1.91 in 2013.
Below is a table of correlations showing the relationships of the rMETRICS in describing BABIP in the current season (BABIP_Y1), predicting in the second (BABIP_Y2), and it’s year-to-year correlation (Y2Y).
| Relationship Between rMETRICS and BABIP, 2002-2013 (min. 300 PA) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BABIP | BABIP | Difference On | |||||||||
| rMETRICS | Y1 | Y2 | Y2Y | BABIP | Y1 | Y2 | Y2Y | BABIP_Y1 | BABIP_Y2 | Y2Y | wSUM |
| rLD | 0.33 | 0.12 | 0.35 | BABIP_LD | 0.37 | 0.02 | 0.12 | -0.04 | 0.10 | 0.23 | 0.173 |
| rFB | 0.65 | 0.35 | 0.70 | BABIP_FB | 0.51 | 0.22 | 0.36 | 0.14 | 0.13 | 0.34 | 0.303 |
| rGB | 0.48 | 0.03 | 0.47 | BABIP_GB | 0.58 | 0.17 | 0.28 | -0.10 | -0.13 | 0.18 | -0.031 |
| rBABIP | 0.80 | 0.33 | 0.52 | BABIP | 1.00 | 0.35 | 0.35 | -0.20 | -0.02 | 0.17 | 0.011 |
Note: “Difference on” = rMETRIC – BABIP in correlation, numbers are correlations (r). wSUM is the weighted sum of difference in BABIP_Y1, BABIP_Y2, and Y2Y with predictive value weighted the highest, then year-to-year correlation, and lastly description.
Across the board, the rMETRICS are more stable year-to-year against BABIP and it’s components, with each metric having a much improved year-to-year correlation. Meanwhile, rFB is the only metric that proves to be more descriptive, predictive, and stable than its counterpart, “BABIP_FB”. rBABIP (the sum of rLD, rFB, and rGB) seems to be more stable than BABIP, but less predictive and descriptive.
So it looks like we have a good measure of FB tendency as it relates to BABIP, but it will take more leg work to get GB and LD and an accumulative BABIP measurement up to speed on the descriptive and predictive levels.
Finding Line Drive and Ground Ball Tendency as it Relates to BABIP — dMETRICS
In order to find a better measurement of line-drive and groundball tendency, I tried to re-incorporate LD%, FB%, and GB%, weighting each rMETRIC by the actual rate in which that batted ball was hit. In doing so, we find the “dMETRICS”. We are looking for the dMETRICS to be better than the BABIP components and also to improve the relation between groundball and line-drive tendency with BABIP.
For example, the dMETRIC for LD will follow the following formula. Remember, this LD% will act as a weight of the probability of a line-drive—which differs from the LD% (excluding HR’s) used in the rLD formula. In other words they won’t cancel.
dLD = rLD *LD%
The dFB and dGB will be found by substituting the “LD” for the proper batted ball.
Below is a table of how the dMETRICS match up with the BABIP statistics.
| Relationship Between dMETRICS and BABIP, 2002-2013 (min. 300 PA) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BABIP | BABIP | Difference On | |||||||||
| dMETRICS | Y1 | Y2 | Y2Y | BABIP | Y1 | Y2 | Y2Y | BABIP_Y1 | BABIP_Y2 | Y2Y | wSUM |
| dLD | 0.93 | 0.35 | 0.40 | BABIP_LD | 0.37 | 0.02 | 0.12 | 0.57 | 0.33 | 0.28 | 0.542 |
| dFB | 0.94 | 0.36 | 0.35 | BABIP_FB | 0.51 | 0.22 | 0.36 | 0.43 | 0.14 | -0.01 | 0.222 |
| dGB | 0.94 | 0.34 | 0.43 | BABIP_GB | 0.58 | 0.17 | 0.28 | 0.37 | 0.18 | 0.14 | 0.307 |
| dBABIP | 0.98 | 0.37 | 0.40 | BABIP | 1.00 | 0.35 | 0.35 | -0.02 | 0.02 | 0.05 | 0.033 |
Note: “Difference on” = dMETRIC – BABIP, numbers are correlations (r).
Here, dLD is a huge improvement over using BABIP_LD in all facets, with the highest wSUM of the sample of 0.542, 33 points more predictive than BABIP_LD among other improvements. Meanwhile, dFB is much more predictive and descriptive than BABIP_FB but misses the cut in year-to-year correlation, proving to be less valuable than rFB above (which had more year-to-year correlation).
dGB improved dramatically over rGB, as well, with a change in weighted sum of around 0.31. It is now positively better across all three categories than BABIP_GB. dBABIP–the sum of dLD, dFB, and dGB–is better across the board at predicting BABIP than rBABIP and a whole lot more descriptive and predictive, but it lacks the year-to-year correlation of rBABIP.
By weighting the rMETRICS by batted-ball rates, we have improved the measurement of hitter tendency in line drives and ground ball, in addition to rFB, which is the best measure of flyball tendency.
Overview of Findings
If you skipped all the math up there and find yourself here, I am going to tell you why you should care about all of this new material.
Batted ball data in it’s current form tells us little about BABIP, which seems counter-intuitive given that you would think batted balls would tell us a lot about a player’s ability to reach base on them. Why you should care is that you want to supplement BABIP with statistics that will actually tell you how to interpret BABIP.
So what I have introduced is simply a new way to use batted-ball data that will give us a better understanding of how BABIP works. This means instead of supplementing a player’s BABIP with his LD% that given year, you may be better off using my personal measure of dLD. Here is why:
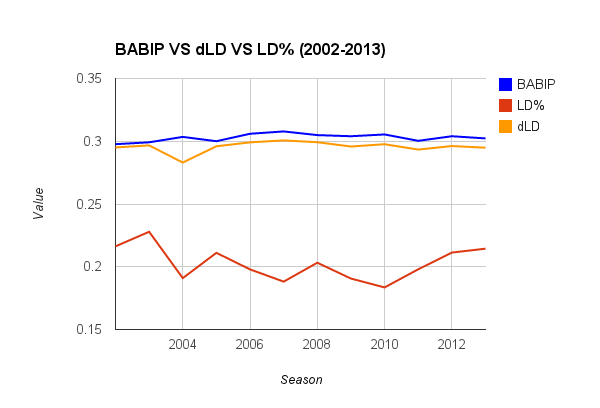
Above you can see dLD is much more descriptive of BABIP than LD%, as it’s line is more similar with BABIP than LD%’s. Not only will dLD better map BABIP in the current season, it also will prove to be a better measure of BABIP in the next season (0.35 predictive, and 0.93 descriptive). So dLD will not only tell you “what you have,” it can determine better than LD% what your “going to get.”
The same thing applies to ground balls. The rate at which they are hit does not tell us much in terms of BABIP. However, with dGB, we now have a great descriptive statistic that also has predictive value. As shown below:

The dGB line is almost symmetrical to the BABIP line in the graph above, meaning that it is very descriptive (0.94) as compared to GB% (0.20 descriptive). In terms of predictability (not deducible from the graph), dGB in year one correlates with BABIP in year two at 34 percent, while GB% sits at 21 percent predictive.
Lastly, FB% and it’s weakness compared to dFB is clearly illustrated in the following graph:
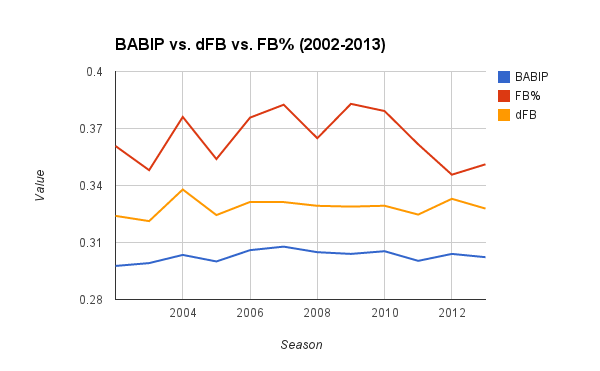
The most similar line to BABIP, unsurprisingly, is dFB, which is 96 percent descriptive with BABIP in the current year. Meanwhile, FB% alone is 51 percent descriptive, so there’s a large improvement in using dFB compared to FB%. In predictive power, dFB correlates at 36 percent with BABIP in the next season, while regular FB% can only correlate at a 27 percent clip.
While dFB is the most effective descriptive measurement for BABIP, it is more effective to use rFB for predictive purposes (as we do below) because it has less yearly variation and slightly more predictive power.
So we now have three new metrics that are huge improvements over using just plain batted-ball rates in rFB, dGB, and dLD. We will call all three of these tendency metrics, or tMETRICS (rFB, dGB, dFB). Below is a table comparing the r-values of the tMETRICS to batted-ball rates:
| Relationship Between tMETRICS And BB Rates, 2002-2013 (min. 300 PA) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| BABIP | BABIP | Difference On | |||||||||
| tMETRICS | Y1 | Y2 | Y2Y | BB Rate | Y1 | Y2 | Y2Y | BABIP_Y1 | BABIP_Y2 | Y2Y | wSUM |
| dLD | 0.93 | 0.35 | 0.40 | LD% | 0.38 | 0.16 | 0.29 | 0.55 | 0.19 | 0.11 | 0.36 |
| rFB | 0.65 | 0.35 | 0.70 | FB% | -0.36 | -0.27 | 0.76 | 0.29 | 0.08 | -0.06 | 0.11 |
| dGB | 0.94 | 0.34 | 0.43 | GB% | 0.20 | 0.21 | 0.77 | 0.74 | 0.13 | -0.35 | 0.14 |
| tBABIP | 0.74 | 0.37 | 0.66 | BABIP | 1.00 | 0.35 | 0.35 | -0.26 | 0.02 | 0.31 | 0.09 |
Note: “Difference on” = tMETRIC – Batted Ball Rate, numbers are correlations (r).
Taking the best metrics from the dMETRICS and rMETRICS series, we have better measures of description and prediction while not sacrificing (too much) year-to-year correlation of simple batted-ball rates. dLD is now 55 points more descriptive and 19 points more predictive while gaining 11 points in year-to-year correlation.
The improvement in LD tendency is great to see considering how LD% is the most inconsistent metric of the batted ball rates (28 percent Y2Y). tBABIP–the sum of dLD, rLD, and dLD–is the best of the bunch when it comes to predicting BABIP. In fact it’s two percent better than BABIP itself at predicting next year’s BABIP and 31 percent more consistent in terms of year-to-year correlation!
Predicting BABIP by Using New Batter Tendency Metrics — pBABIP
Given the improvement in finding batted-ball metrics that actually have predictive and descriptive value when it comes to BABIP, we can use them as variables to better predict BABIP year to year.
The following are the components that I included in pBABIP, my personal predictive model:
- Batted Ball Tendency — Using dBABIP, we can accurately (relative to original batted-ball metrics) describe and predict batted-ball tendency related to BABIP. I also used FB*IFFB, which finds the percentage of infield fly balls relative to the entire ball-in-play distribution. Both correlate highly to BABIP in year 2. The choice of dBABIP over tBABIP is because dBABIP remains more descriptive at the same level of prediction. rGB/rFB or GB/FB rate was not included because, with dBABIP already in the regression, it becomes a superfluous factor.
- Power — In order to map power (or lack thereof), I used ISO (batting average minus slugging percentage) over HR/FB because FB was a component of dBABIP already. ISO is considered a crude measurement of batted-ball speed.
- Speed — Using the FanGraphs’ “Spd” metric, I included a player’s measurable speed, which factors in to a player’s ball-in-play distribution and the rate at which he reaches base via ground balls and other batted-ball types.
- Spray — To measure spray, I used the ratio of pulled batted balls to center field batted balls. Then I incorporated the number of pulled balls and opposite field batted balls. Including these numbers should account for players who know how to play themselves out of shifts and use the field to their advantage.
Using a 300-PA cutoff from the 2002-2013 sample, these variables yielded this linear model:
pBABIP = 0.2686+0.1593*dBABIP+-0.3377*(FB*IFFB)+0.002389*ISO+0.0774*Spd+-0.0006532*Pull+0.0003829*OPP+-0.0006263*Center+(Pull*Center)*0.00001038
For the mathematically inclined, pBABIP is significant on the highest level (p-value nearing zero :< 2.2e-16). Each input ranked on the highest level of significance in the regression (a p-value nearing zero or “***” in R).
Using this above model, pBABIP predicted 22 percent (r^2) of the year-to-year change in BABIP over the 2002-2013 sample and 23 percent (r^2) in the 2004-2008 sample used in Derek Carty’s study. For the 2012-2013 sample, pBABIP was able to predict 30 percent of the variation in BABIP with a 300-PA cutoff. This means pBABIP could predict variation at a 10-18 percent higher clip than using BABIP itself to predict next season’s figure.
Typically, the most accurate model to predict BABIP is xBABIP, which predicted 25 percent of the variation in BABIP in the 2004-2008 sample of 300 PA as conducted in Carty’s study on the best BABIP estimators. The 25 percent number is an impressive one considering xBABIP uses just one year’s previous data to predict the next season’s BABIP, not a three-year weighted average like other BABIP estimators. xBABIP is great, but it is hard to calculate and is not easily accessible.
pBABIP comes in at about two percent below xBABIP in predictive power, based on the 20o4-2008 sample study conducted by Carty. However, the power of pBABIP is in its simplicity of design and the credence it gives to our newly formed batted-ball metrics, which have a much-improved relationship with BABIP. Substitute dLD, rFB, and dGB (dBABIP) in our model with LD%, GB%, and FB%, and you would see a large drop-off in its predictive value.
The matter of the fact is, no BABIP model uses batted-ball metrics quite as effectively as pBABIP. Coupled with the simplicity of its design, there remains a lot of room to grow.
Next Steps
This is only what I hope to be the beginning of an ever-evolving model. There are many other factors to consider that could very well close or leap-frog the gap between pBABIP and xBABIP. Those include what were suggested by Christopher D. Long, who has suggested that a BABIP model needs to include, but not be limited to, the following:
- Adjusting for pitcher-neutral ball-in-play (BIP) distribution
- Defensive positioning and shift/status.
- Horizontal/vertical measures of a batted ball.
I will also consider the following factors in the future as components that could have predictive gains:
- Hang time and batted-ball location via the new FanGraphs spray charts.
- Adjusting for park and league factors.
Inclusion of the above can make pBABIP, which already is very close in accuracy to the top BABIP estimator, the go-to estimator for batted-ball prediction. Quantifying the above factors and including them into the pBABIP model will serve as the basis for my future articles.
Data located here: Use new batted ball metrics to create your own pBABIP formula.

Nice Max – gracefully & insightfully written…I actually already incorporate this into my projected avg (vs. The xavg approach to BA that incorporates xBABIP) for my projections…I don’t like using xavg b/c of guys like EE, kinsler, etc.
But I wouldn’t have been able to explain it like this!
Prob not explained well enough in my first reponse…I took each bip type “hit expectancy” / player individual hit% on each balls in play type and that’s my xBABIP (also projected the xbabip prior to this for comparison sake to see who was really distinguishable) and will eventually post on why…hoping to incorporate the same factors you noted at the end. Thanks again.
So sounds like a variation of bMETRIC that you included in your model (% of hits in play). If you’d like an actual spreadsheet of pBABIP—email me. I’d be interested to know how accurate your measure is compared to pBABIP. Thanks for reading!
Hey Max, shouldn’t that name be Einstein? Very impressive work.
Thanks, Jim…
Born a “W” away from brilliance.
Impressive work. Will have to read through this a few more times to get all nuances. I do like the idea of incorporating other factors, but incorporating park factors would only account for FB%, or, at least, have the greatest effect here.
Also just noticed one small subtraction error… Your dGB values seem to be off by 0.01. It is like the 0.111958% that cannot be explained by Walter White when he catalogues the human body 🙂
Outstanding article, Max. Can’t wait to re-read it a few times and incorporate it into our research.
OK, I’m hooked. More!
Excellent!
Funny thing is, I had thought about the possibility of refining UZR and similar defensive metrics by adjusting the expected values in each zone by something like the weighted average of batter-specific bMETRICs, to account for the fact that a grounder between 1st and 2nd by say Ryan Howard is more likely to be a hit than one by say Brendan Ryan.
But you’ve done something way more useful and more elegant than this, and used this to get at the core components of batted-ball performance for hitters, and at a level that allows for reasonable sample sizes on the key drivers. The end result is something that could be very useful for many purposes.
Very interesting stuff. But in the formula dLD = rLD * LD%,
what does the * signify? I thought it was a multiply sign, but that doesn’t work, because
bLD = P (LD|H) = BABIP_LD x LD%/(H/PA)
and rLD = BABIP_LD/bLD
= BABIP_LD/ [BABIP¬_LD x LD%/(H/PA)]
= (H/PA)/ LD%
if * were a multiplier sign, then dLD = H/PA
Yeah, didn’t make this clear it is multiplying by LD% including HR — so basic P(LD/BIP).. So dLD = (H/PA * LD%)/LD%* if you break it down…
So if a player doesn’t hit any HRs (and a light hitter like Visquel I guess approaches that), then dLD = H/PA?
Yes that’s a big issue—one of the reasons it’s out of 350 PA. Something I need to address and will do when other data becomes available to me. Power of dMETRICS seems to be more predictive nonetheless.
Also, can’t these formulae be stream-lined?
bLD = (BABIP_LD x LD%)/(H/PA) = (BABIP_LD x LD)/H,
where LD is just the total number of LDs, since PAs cancel out.
And as I noted in my previous post,
rLD = (H/PA)/ LD% = H/LD, as again, PAs cancel out.
Yeah, it could be streamlined — just wanted to show though process and progression.
SO rLD = H/LD and dLD = (H*LD)/(LD*PA).
Thanks–and understood. The progression was important. As a whole, the article was really great. I think you’re always onto something important when you show how something that appears intuitively so–high line drive rate, therefore high BABIP–is not in fact necessarily the case.
SO rLD = H/LD and dLD = (H*LD)/(LD*PA).
So doesn’t that mean dLD = H/PA once you cancel out the LD that is both the numerator and denominator? Have you gone through all these mathematical gyrations just to discover that BABIP correlates very well with BA?
Sorry Peter, didn’t make that clear above…
It should be (H_not_HR*LDw/HR)/( LDw/oHR * BIP(all)).
rLD = H/LDw/oHR andLD% ~ LD/BIP
Hence, rLD and rGB are so similar — also no way it’s a complicated form of H/PA given the correlations w/ BABIP and that rLD!=rFB!=rGB!=H/PA. If you had H/LD(all) as rLD then you would have everything cancel to H/PA, which is far from desired.
LD% is out of BIP, P(LD) used in bLD -> LD/PA where LD != HR.
It should be (H_not_HR*LDw/HR)/( LDw/oHR * BIP(all)).
So this simplifies to dLD =(H woHR/BIP)*(LDwHR/LDwoHR)
Since LD HRs average about 3 percent of all LDs this simplifies to dLD=BABIP*(1/.97) = dLD=1.03* BABIP. This would vary of course with each player’s rate of LD_HR per LD but not much. Fifty percent of the 237 qualifying batters had LD_HR per LD rates less that 3 percent and more than 94 percent had a rate of less than 10 percent.
Or maybe I didn’t pay attention to when you include HRs, and when not. Will have to go over this again.
Can you correlate BABIP to the player’s average bat speed? The idea is that a player who maximizes bat speed must commit sooner, before he knows exactly what the speed and location will be when the pitch crosses the plate, therefore his timing is more based on guessing which increases the spray of the ball and makes BABIP look more like “luck.” My hypothesis is that a batter who wants to aim for a high BABIP would presumably need to watch the pitch longer and swing later with less speed. My guess would be that batters who intentionally try for high BABIP don’t make it to the majors where slugging percentage is regarded as being more important, probably for a very good reason, hence BABIP is not predictive.
Couldn’t you argue the reverse? The faster the batter gets the bat around, the longer he can wait?
I think it is generally accepted that batters with more bat speed can wait longer… it would seem hitters are forced into guessing when they can’t get around on pitches taking the time they need to recognize pitches. That is what makes pitchers with high 90’s heat with a spot up second or third pitch so devastating. It’s also what makes a hitter with a comparatively slow bat so devastating to his lineup.
If I am reading your tMetric chart correctly you are showing an r of .37 in predicting year 2 BABIP using your best tMetrics. Using year 1 BABIP to predict year 2 BABIP results in an r of .35. r squared would then be .136 for tMetrics and .123 for BABIP. Is this correct? It would be interesting to see how this incremental increase in r squared translates into average mean error of year 2 predictions of BABIP.
The formula you used to mean the conditional probability of a LD, given it’s a hit — the very first formula, way up at the top — is wrong.
In the numerator, you use LD%, which is a percentage of batted balls. But in the denominator, you switch to H/PA, which is a percentage of plate appearances.
You need to be consistent about your universe for the math to actually work out. Sorry.
LD%* is what I call LD/PA not resulting in a HR… Denominator is consistent, in that case.
I made that clear in the comments, not in the article.
LD% is out of BIP, P(LD) used in bLD -> LD/PA where LD != HR.