Sacrificing in 2005 Redux
For just a moment I hesitated while writing the article “Not So Sweet Surrender.” I knew that discussing the merits of the sacrifice among baseball fans would be a bit like debating the various theories of mass extinction at the end of the Permian period among paleontologists—that is, a discussion overflowing with opinion but absent a whole lot of concrete information. But in the end I plunged into the water and laid out some basic facts regarding sacrifice attempts, successes and how they relate to the standard argument against sacrificing used by many sabermetricians.
But like a paleontologist who often needs to go back into the field to uncover more fossils in order to provide a more robust interpretation, a sabermetrician or “performance analyst” usually needs to build on his data in order to be more certain in his analysis.
And so it is in that spirit that this week I present a few more fossils related to sacrifices from the play-by-play data for 2005 and answer a few of the questions on the minds of readers.
Slicing Through the Strata
Several readers noted that I mentioned in the initial article that the sacrifice success rate for pitchers was less than that for position players but failed to quantify that statement. The following table lists the attempts, successes (defined as a successful sacrifice or the defense recording zero outs on the play) and the percentage by position.
Pos Att Succ Pct
1B 47 41 0.872
LF 138 119 0.862
DH 27 23 0.852
2B 264 224 0.848
C 170 143 0.841
CF 230 193 0.839
RF 77 62 0.805
SS 305 244 0.800
3B 128 101 0.789
PH 82 62 0.756
P 887 582 0.656
2355 1794 0.762
Interestingly, first basemen and designated hitters come out first and third, although the sample size is small. Could the element of surprise as a lumbering power hitter lays down a bunt play a role here?
Also, you can see that all three outfield spots were successful more frequently than shortstops, while catchers ranked a somewhat surprising fifth. Neither of these are results I would have expected, since middle infielders are often assumed to be better handlers of the bat.
Pitchers were expected to come in last, although the fact that they were 10% worse than any position player was a larger gap than expected. Overall, position players were successful 82.6% of the time (1,212 of 1,468), a full 17% better than pitchers. As hinted at in the previous article, however, more than half this difference can be attributed to the fact that managers “ask” pitchers to bunt much more frequently with two strikes than they do position players, resulting in many more strikeouts. When those attempts are subtracted, pitchers are successful 76% of the time.
Of course once we slice the data by position we might as well do so for inning and score as shown in the following two tables.
By Inning
Att Succ Pct
1 155 140 0.903
2 250 174 0.696
3 318 224 0.704
4 215 165 0.767
5 305 212 0.695
6 221 177 0.801
7 276 214 0.775
8 304 235 0.773
9 201 168 0.836
10 50 45 0.900
11 28 18 0.643
12 24 17 0.708
13 4 3 0.750
14 1 0 0.000
15 2 2 1.000
16 1 0 0.000
By Score Score Att Succ Pct <=-5 21 16 0.909 -4 23 17 0.739 -3 54 39 0.722 -2 138 100 0.725 -1 377 290 0.769 0 809 633 0.782 1 352 257 0.730 2 284 219 0.771 3 158 118 0.747 4 80 64 0.800 >=5 59 41 0.750
What you’ll notice here is that managers don’t seem to have a preference for what inning they sacrifice in (except perhaps the first), while they certainly do have a preference based on the score. It’s interesting that almost a third (31%) of all sacrifice attempts in 2005 occurred before the fourth inning.
Earl Weaver would not be pleased.
What this likely reflects is the convergence of two factors: first, the prevalent idea that “getting on top” early puts the opponent at a greater disadvantage (perhaps psychologically and strategically) than the score would otherwise indicate, and second, the fact that starting pitchers come to bat a greater percentage of the time in the early innings than they do later in the game. While I haven’t looked into the first factor (although others have), the following table backs up the second factor by showing that over 60% of pitchers’ sacrifices occur in the fourth inning or before and 80% occur before the sixth inning.
Inning Att Pct
1 4 0.005
2 188 0.212
3 212 0.239
4 133 0.150
5 180 0.203
6 88 0.099
7 55 0.062
8 20 0.023
9 3 0.003
12 4 0.005
The high success rate in the first inning is due to the fact that pitchers aren’t typically sacrificing in the first inning, when the work is usually being done, and done quite well I might add, by the second hitter in the lineup.
The following graph shows the sacrifice attempts by score differential.
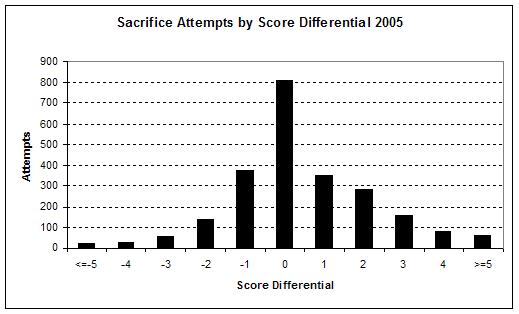
No surprise here. Over a third of all sacrifice attempts occur when the score is tied and managers are reluctant to sacrifice when down by more than one run (just 10% of attempts). Managers will continue to sacrifice, however, when ahead, and they even did so about 140 times when up by four or more runs. You can never have enough runs.
Along with the breakdown by inning and position, several readers wanted to know what individuals were the most successful because I’d teased them with a list of players who had the most attempts. The following two tables show the leaders and trailers in sacrifice percentage for those with 10 or more attempts.
Leaders
Att Succ Pct
Dave Roberts 13 13 1.000
Derek Jeter 10 10 1.000
Kenny Lofton 10 10 1.000
Luis Castillo 19 19 1.000
Miguel Cairo 12 12 1.000
Nick Punto 10 10 1.000
Nook Logan 16 15 0.938
Tadahito Iguchi 13 12 0.923
Juan Uribe 13 12 0.923
Omar Vizquel 25 23 0.920
Cory Sullivan 12 11 0.917
Angel Berroa 12 11 0.917
Aaron Miles 11 10 0.909
Randy Winn 11 10 0.909
Kyle Davies 11 10 0.909
Juan Castro 11 10 0.909
Nick Green 11 10 0.909
Alex Sanchez 10 9 0.900
Andy Pettitte 17 15 0.882
Jack Wilson 15 13 0.867
Trailers
Att Succ Pct
Doug Davis 10 2 0.200
Jon Lieber 10 3 0.300
Josh Beckett 11 4 0.364
Mark Redman 10 4 0.400
Ramon Ortiz 15 6 0.400
Eric Milton 12 5 0.417
Chris Carpenter 20 10 0.500
Victor Zambrano 10 5 0.500
Pedro Martinez 12 6 0.500
Esteban Loaiza 13 7 0.538
Jeff Francis 11 6 0.545
Brad Halsey 11 6 0.545
AJ Burnett 16 9 0.563
Greg Maddux 12 7 0.583
Ben Sheets 11 7 0.636
Roy Oswalt 11 7 0.636
Royce Clayton 15 10 0.667
Woody Williams 12 8 0.667
Brandon Webb 19 13 0.684
Cristian Guzman 13 9 0.692
Not a lot of surprises in these lists either. The leaders are speedy position players with good bat control, with the exception of pitchers Andy Pettitte and Kyle Davies, and the trailers are a bunch of pitchers, with the exception of Royce Clayton and Cristian Guzman. (Did anything go right for him in 2005?) I was a bit surprised to see Greg Maddux on the list, although obviously the small number of attempts doesn’t lead to any forceful conclusions.
Run Expectancy and Scoring Probability
There were several readers who expressed a bit of consternation over the following cryptic paragraph in the initial article:
“Of course the above is based on the assumption that an average hitter is at the plate. Pitchers are the most often called upon to sacrifice, and they are anything but average. We can adjust for that as well by adjusting the probability of success based on an average pitcher’s performance.”
The questions that arose from this were generally related to how this bit of magic was done and if it was done by adjusting the Run Expectancy or Scoring Probability matrices for pitchers. The short answer is yes. The long answer follows.
You’ll remember that both matrices (I showed the Scoring Probability matrix for the period 1999-2002 in the initial article) are based on the average hitter, therefore taking into account both pitchers and position players. If the matrices only included pitchers, then obviously the values in the matrix (the number of expected runs and the probability of scoring runs) would be lower since pitchers don’t move runners around the bases as efficiently as other hitters. As a result the break-even percentages for attempting a sacrifice, stolen base or any other strategic option would correspondingly be lower since the cost of failure is lower with a pitcher at the plate. In economic terms, the opportunity cost for each pitcher plate appearance is less than that for an average hitter, so it is more often beneficial to sacrifice an out for a base.
Because of this fact it’s clearly not fair to decide whether pitchers should sacrifice by looking at the standard matrices. So what I did was adjust the individual cells of each matrix for pitchers by multiplying their average outcomes by the run expectancy or probability of scoring given each outcome and then summing the results.
To illustrate this process let’s look at the situation when a runner is on first and there is nobody out. According to the Scoring Probability matrix, in this base/out situation, there is a 43.7% chance of scoring in the remainder of the inning. Since this is too high when a pitcher is at the plate, we’ll first break down the average pitcher’s outcomes by plate appearance like so:
Out .798 Single .120 Double .027 Triple .002 Homerun .008 Walk .047
This represents the performance of an average pitcher from 1999-2002.
We can then multiply each of these probabilities by the probability of scoring given each outcome. For example, a pitcher makes an out .798 of the time, so we’ll multiply that by .283 which is the resulting scoring probability if the sacrifice fails (with failure being defined as resulting in a runner on first with one out) for a value of .226. We can then do likewise for each of the outcomes shown above.
Outs 0.798 0.283 0.226 1B 0.120 0.641 0.077 2B 0.027 0.876 0.024 3B 0.002 1.000 0.002 HR 0.008 1.000 0.008 BB 0.047 0.641 0.030 Total 0.367
Granted we need to make a few assumptions here regarding the base/out situation after each outcome, but overall this will give us the approximate probability of each base/out situation occurring after the pitcher’s plate appearance.
We can then add all of these up to come up with the scoring probability of 36.7% when a pitcher is at the plate. In other words, the chances of scoring drop by 7%. You’ll note that this drop is confined to the impact of the pitcher since we’ve use the standard probabilities in the calculation above to represent the outcomes for the remainder of the inning.
This lower number is then used in the calculation of the break-even percentage as Pv in the equation:
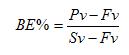
where Pv = Present Value, Fv = Failure Value, and Sv = Success Value.
So with a man on first and nobody out, the BE% for an average hitter would be calculated as:
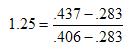
while for a pitcher the calculation would be:
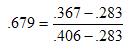
In other words, with a pitcher hitting, the sacrifice attempt needs to be successful 67.9% of the time, while for an average hitter it’s “always” more cost effective to swing away.
Several other readers, however, pointed out that these matrices, are based on the aggregate of all situations, and all hitters don’t reflect the many nuances of the game, many of which drive these strategic decisions. Absolutely correct. If you wanted to create a perfect model there wouldn’t be a single matrix but rather dynamic matrices that would morph to include the effects of team, park, pitcher, speed on the bases, defensive positioning, score, weather and the next hitters in the lineup, as well as every other data point you can think of. Just as physicists use models to describe physical reality, the standard matrices are simply a model or approximation of the more complex reality on the diamond. The analyses derived from them are therefore useful for narrowing the range of possible answers to specific questions, which we hope at least get us in the ballpark so to speak.
Finally, thinking along these lines, another astute reader pointed out that while I included in my definition of a successful sacrifice events when no outs were recorded by the defense, I then compared this to the break-even percentage, which does not include these “very successful” sacrifice attempts. Once again, that is absolutely the case and the calculations in the previous article were first-order approximations.
In order to be more precise one would have to calculate derivative matrices that weighted the actual outcomes from sacrifice attempts. For example, in 2005 with a runner on first and nobody out we can break down the percentage of sacrifice attempts that were successful under my definitions as follows:
When calculating the break-even percentage, our Sv, instead of the typical .406 (runner on second and one out), would be raised to:
However, 5% of all unsuccessful attempts resulted in a double play, so the failure value Sv would be calculated as:
instead of .283. Plugging these new values into the break-even formula for an average hitter gives us:
So instead of never being a good idea to sacrifice in this situation, it would in fact make sense if you were successful more than 19 times out of 20. Applying this same procedure to a pitcher you get a break-even percentage of .549, so sacrificing with a pitcher does indeed continue to literally be a “percentage play.”
Overall this procedure has the effect of lowering the break-even percentages and thereby making the sacrifice a more attractive option. I didn’t perform these calculations in the initial article, but had I done so the break-even percentages for the following situations would have been attractive for average hitters:
Base/Out Break-Even% 12/0 .723 2/0 .777
Once again, however, this doesn’t factor in the many other variables mentioned previously. But of course that’s one of the beauties of baseball. As much as baseball being a game of discrete events lends itself to analysis, there’s always plenty more that eludes us. For now anyway.
