Some Physics of Losing a Fly Ball

On April 8, 2019, in the top of the fourth at Coors Field, the remarkably reliable Charlie Blackmon dropped an unusually high fly ball hit by Cody Bellinger. Here’s the video:

The ESPN broadcast team immediately went searching for explanations (or excuses, depending upon your point of view). The play-by-play announcer (probably Matt Vasgersian) blamed the new LED lights. Alex Rodriguez opined, “This ball was so high, I’m sure he had a hard time seeing this ball.”

The ESPN production staff quickly prepared an impressive graphics sequence using the Statcast data on the fly ball. (Unfortunately, this video is not available unless you watch the entire broadcast.) Statcast reported a launch angle of 50˚, an exit velocity of 105.2 mph, a hang time of 6.8 seconds, and a maximum height of 172 feet. As the graphic was displayed, Jessica Mendoza said, “I feel like if it was lost, it wasn’t in the lights. It was in the dark sky because you just don’t see fly balls hit that high.”

Blackmon didn’t really react like he lost the ball. He moved in the typical way outfielders do when they are tracking a ball well, and the ball did hit his glove. Neither could I find any comments he made regarding the play after the game. So we don’t really know if he lost the ball in the lights, if he lost it in the dark, or if he saw it all the way and just didn’t make the catch. Since we have no definitive answers as to the cause of the error, let’s see what physics has to say about losing sight of a ball.

The Rayleigh Criterion describes the maximum distance away an object can be seen under ideal circumstances. Spoiler alert: While the human eye is very good, it is not quite ideal in this sense. The Rayleigh Criterion requires:

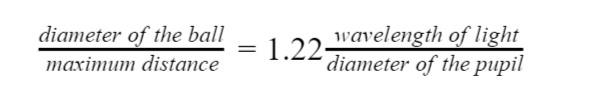
(Don’t ask where the 1.22 comes from — you’ll be sorry you did.)

We’ll use the average wavelength of visible light and a value for the size of the pupil – that’s the black hole in the center of the eye that lets in the light. Pupil size varies from person to person. In the dark, the average is about 5 mm.

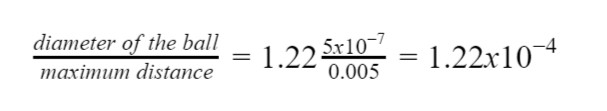
Using three inches for the diameter of the ball gives us an estimate of the maximum distance at which a person could see a baseball under ideal circumstances.

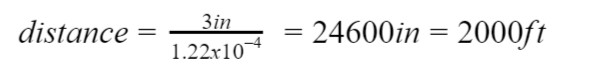
That is a crazy big number, but remember: This is for an ideal situation, like a well-lit ball with a high-contrast black background. It is perfectly plausible one could see a ball 173 feet up, assuming the lighting is reasonable. I suppose we already knew this, because we rarely have seats fewer than 173 feet from the ball, and most of us can watch the ball without a problem during a night game.

The next question relates to the amount of light actually on the ball. Luckily, I literally have friends in high places, so I know the light towers at Coors Field are 175 feet tall. You might then assume the fly ball in question was lit up throughout its journey, because it never got above the lights. That would be correct — except for the fact that the lights on the towers point downward to illuminate the field and the stands, leaving a lot of space above the stadium in the dark. So while the ball never got higher than the light towers, it was above the light they provide, at least for the highest portion of its flight.

It is interesting to think about the way stadiums are lit from the top down. If you were in a dark room and shone a flashlight toward a baseball, you would see the ball is only about half-lit. The side facing the flashlight is bright, while the other half – the one away from the flashlight – is dark. So, in a ballpark, the lighting is such that the bottom of the ball is never directly illuminated by the lights.

Here I go…off on a tangent. Set the flashlight on a shelf or table shining across the otherwise dark room. If you position yourself between the flashlight and the ball without blocking the light, it will appear to you that the ball is completely lit because you only see the lit side. You can’t view the dark side from this position.

Now, rotate around so the ball is between you and the light. The ball appears to be completely dark because you are not viewing the side that is lit. Rotate very slowly back to being between the ball and the flashlight. You will see the ball go from being completely dark to a lit crescent, to half-lit, to mostly lit, then finally, fully lit. You now understand the phases of the moon!

Back to the ballpark. Each individual light on the light stanchions is almost always above the ball and only lights up the half of the ball on the side directly facing the light itself. Since the field has many such lights, a good portion of the ball will be bright. However, the very bottom of the ball will never be lit directly by the stadium lights.

So, why have you never heard an outfielder comment on this? I suspect they have never really thought about it. They know what a fly ball looks like at night from decades of experience on the field, not years in physics classrooms. Besides, there are secondary sources of light that can shine on the bottom of the ball.

It turns out that illuminated objects absorb some colors of light and reflect others. The stadium lights look white to our eyes because they emit all the colors of the rainbow. The baseball appears white to our eyes because it reflects all those colors. However, the grass is green because it absorbs all colors of light except green, which it reflects. Similarly, your team’s jersey looks red because it absorbs all colors of light except red.

At this point, you would probably prefer to get back to baseball and talk about Albies, Almora, or Alonso. Instead, we need to discuss Albedo. Albedo is effectively the fraction of light reflected by an object. If you Google the word “albedo,” most of the hits are associated with climate change and global warming.

If you think of Earth as a whole, sunlight illuminates our planet while, at the same time, we reflect light back out into space. This light can be seen in the famous photo taken of Earthrise from the moon. The ratio of the outgoing light to the incoming light – the albedo – has a lot to say about the average temperature of our dear little orb.

Back at Coors Field, the fly ball hit to Blackmon was above the effect of the stadium lights, and we were trying to estimate the amount of reflected light from the field that might have illuminated the bottom of the ball. Knowing the albedo of grass is about 25%, we would expect the light on the bottom of the ball would be about a quarter of the amount the sides would have at lower altitudes. In addition, this light would be more greenish than white.

So it is possible the bottom of the ball was dimmed enough that Blackmon could have lost it in the dark, although we can’t say for sure. Since Blackmon didn’t seem to shed any light on the matter himself, we are left in the dark to speculate. On the bright side, we got to think about the Rayleigh Criterion, the phases of the moon, climate change, the color of your team’s jersey, and the challenges of the game at night. I hope you’ve found the discussion illuminating.