The Exponential Nature of Offense

Baseball has countless old sayings, some of them accurate. One of those sayings is “hitting is contagious.” The spirit of this saying has to do with a lineup getting hot at the same time during a season, or creating a rally during a game. In those contexts, the saying may or may not be true (an article for a different day, perhaps), but I submit that offense is contagious in a general sense. Good offenses are better than the sum of their parts – one and one equaling more than two.

The exponential nature of offense means a good hitter in a good lineup is worth more than that same hitter in a bad lineup. On a good offense, that hitter is more likely to come to the plate with more runners on, more likely to get driven in once he’s on base.  And, the lineup turns over more often, meaning he gets more plate appearances. Not only is he more valuable to a good lineup, but he’s even more valuable to a better one – the effect builds on itself.

The lineup-turnover part of this effect can be seen in the below graph, where plate appearances and runs scored go hand in hand for all teams (that played 162 games) between 1973 and 2013.

Scoring more runs has always been preferable to scoring fewer, so why does this matter? How could a team use this information to its advantage? Consider this: Offensive statistics, even advanced ones, are built on linear models. This means there are blind spots, where the stats over-or-underestimate actual production. An innovative team could take advantage of this fact, and pay less than market value for offensive production.

Proof That Offense Is Exponential

First, let’s look for the mathematical evidence that offense is non-linear. This is probably the boring part, but it needs to be done.

One way to examine the relationship between offensive talent and offensive production is to find the elasticity between the two variables. Taking every team between 1973 and 2013, I created a model with the natural log of runs scored per game as the dependent variable and the natural log of weighted on base average (wOBA) as the independent variable. I also included base running value per game (BsR/G) as an independent variable to control for running skill, since wOBA doesn’t account for anything on the base paths. The coefficient of the Ln(wOBA) variable represents the elasticity between offensive skill, as measured by wOBA, and production, as measured by RS/G. There are three possibilities for the coefficient in question:

1. The coefficient is less than one, meaning there are decreasing returns to scale – increasing wOBA by 10 percent will lead to fewer than 10 percent more runs scored.
2. The coefficient is exactly one then there is a linear relationship – increasing wOBA by 10 percent will lead to 10 percent more runs scored. If wOBA were a perfect measure of production for every team, this would be the case.
3. The coefficient is greater than one, meaning there are increasing returns to scale -– increasing wOBA by 10 percent will lead to more than 10 percent more runs

You guessed it, the coefficient falls into the third group. The regression results are below:

Regression output, predicting the natural log of runs scored per game

Predictor	Coefficient	T-Score
Constant	4.1331	149.6
Ln (wOBA)	2.3342	95.5
BSR/162	0.0014	8.7

The coefficient is 2.33, which can be interpreted as a 10 percent increase in wOBA will result in 23 percent more runs scored per game. The evidence of an exponential relationship is clear, and large enough to be significantly different from the linear trend.

wOBA Isn’t Wrong, But It Isn’t Perfect

One of the jobs of advanced statistics is to remove context – to measure a player’s skills independent of his team, park, league, etc. This helps to evaluate a player’s true talent level and create statistics which are more predictive of future performance.

Weighted On Base Average is probably the most accurate measure of offensive production ever created. There have been some great articles written on the merits of wOBA, including a primer here, and a recent Hardball Times article here.

Simply put, wOBA does an excellent job of measuring the quality of an offense. Plotting team wOBA against the team’s runs scored per game for every team between 1973-2013 yields the linear-looking trend below.

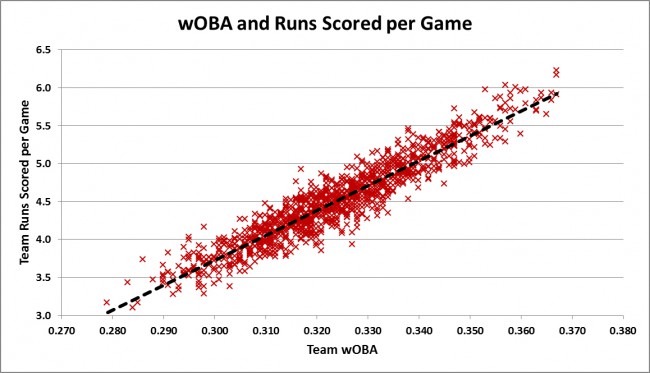
This is the same data I used in the model earlier. You might be asking yourself, “Where is the exponential shape?” Although the trend looks linear, it actually is slightly curved. Discerning viewers might be able to see how the linear trend line cuts below the majority of points below .300 wOBA and above .350.

It is easier to see this effect more obviously with a different graph. This time, I ran a purely linear model with RS/G as the dependent variable and wOBA and BSR/G as the independent variables. I then examined the residuals of that model (the difference between the actual and predicted values of RS/G). I created groups of similar teams, those who had the same first two digits of wOBA (.310s, .320s, .330s, etc.). If the offensive effect is truly linear, then the residuals should sum to about zero for each group. As you can see in the graph below, they do not.

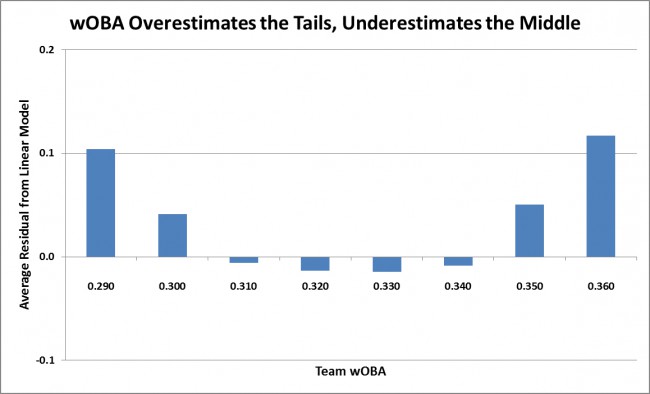
Why? wOBA is calculated using the average run value of an event – the average single, the average double, etc. Doing so strips out the context of the team involved in the event. This is not a flaw; it is exactly what wOBA is designed to do. However, it forces a linear relationship where one does not necessarily exist.

Going back to the above graph, you can see the groups at the top and bottom of the spectrum are underestimated by about one-tenth of a run per game, and the teams near the mean are overestimated by about one-hundredth of a run per game. Why less in the middle than the ends? There are more teams there. Offense in baseball follows a normal distribution, where there are more teams near the average and fewer teams on the extremes. Since there are more teams near the middle, the linear trend fits those teams closer.

This graph likely raises another question: why are both tails underestimated? If offense is exponential, shouldn’t it overestimate the low end and underestimate the high end? The answer is similar to the one in the last paragraph. If you think about a curve, a straight line can estimate only one section of it well. Since teams are bunched in the middle, that is where the line gravitates toward. If, for example, teams were bunched at the low end of the spectrum, then the linear trend would fit that section better, and the middle and upper parts of the spectrum would be underestimated.

Over 1,000 words of explanation leads to this: a team with a .365 wOBA would be predicted to score about 5.85 runs per game, but will actually score about 5.93 runs per game. On the low end, a team with a .285 wOBA would be predicted to score about 3.24 runs per game, but would instead score about 3.33 runs per game. Those are small differences, but remember that baseball has the longest regular season of all major sports. A difference of .09 runs per game equals about 14.6 runs per season, or about one-and-a-half wins. If one team is using the accurate exponential model, while all others value talent using an “incorrect” linear model, it would equate to over $10 million of value for a team on either tail of the spectrum.

Of course, wOBA is not the only statistic that teams use. A stat such as wRC+ is better than wOBA at discovering a player or team’s true talent level, because it is park and league adjusted. However, wRC+ is also based on the linear weights, which use average event values, meaning it will have the same fitting problem that wOBA has – underestimating the tails, overestimating the middle.

How Can a Team Take Advantage?

The results of this analysis mean teams should stop trying to be well-rounded. Today, when a team has a good offense, it usually targets pitching, and when it has good pitching, it usually targets hitting. This is inefficient. Even if the linear trends were completely accurate, teams should be indifferent between a run saved and a run scored. This analysis suggests that a team with good hitting should not only be indifferent, but should actively target more offense.

Here’s where things get a little theoretical. The highest team wOBA in the past 40 years is .367, accomplished by the 1996 Mariners, the 1996 Indians and the 1999 Indians. These teams benefited from about .1 runs per game due to the exponential effect – in excess of the “sum of the parts.” One wonders about a team that went all-in on this strategy and devoted all its resources to offense. It would help if the team played in a hitter’s park as well. If this theoretical team (I’m looking at you, Rockies and Rangers) could push its wOBA to .375, it would yield about .15 surplus runs per game, worth 2.5 wins over the course of a season, or about $17.5 million in value.

The other possibility would be a team going the other direction, using all its resources on run prevention, and embracing a terrible offense. This would lead to a similar surplus over market value, about .1 more runs per game than market price, but teams at that end of the spectrum are not buying free agent hitters anyway, so market value does not apply. Further, it would mean allocating more resources toward pitching, which has proven to be a risky investment.

The biggest conclusion from this analysis is to remember that context matters. Advanced statistics strip away context, which is critical to evaluating players, but it does not mean these stats should always be viewed in a vacuum. Just as a win is more valuable to a team in the middle of the win probability curve, a hitter is more valuable to a team that already has a good offense.

The debate over how best to measure offense is far from new. There have been countless articles written touting the benefits and pointing out the errors of linear weights, runs created formulas, and other methods. I’d encourage anyone to read further these topics here, here and here. The key takeaway from this article is to remember that context matters. When evaluating the value a hitter can bring to a team, the quality of the team’s offense should be a factor, just as is how a park’s dimensions might affect that player.