The Physics of Base Stealing

A lot of science goes into something seemingly as simple as stealing a base. (via Dirk Hansen)
I’m sitting here trying to write something useful about the physics of base stealing, but I can’t because this place is a bigger mess than a clubhouse after winning the World Series. Seriously, it looks like a memorabilia shop exploded.
There are stacks of old ticket stubs, mountains of ballpark giveaways, and 90–yes I’m sure, exactly 90–signed balls in their plastic boxes strewn about somewhere. I’ve had it! I’m going to collect those baseballs and build a shelf for them.
I could place the boxes side by side 90 balls long or I could stack them two high and make a shelf only 45 boxes long. Wow, there are lots of combinations: 30 x 3, 18 x 5, 15 x 6, 10 x 9 … oh and, of course, I could make them taller than they are wide; 9 x 10, 6 x 15, 5 x 18 … no matter what I decide, there still will be 90 boxes. Figure 1 is an example of nine columns of baseballs stacked 10 boxes high.

There are also 90 feet between bases no matter how fast you travel from one to the next. If you jog at 18 feet per second, it will take five seconds, at 15 feet per second, it will take six seconds, at 10 feet per second it takes nine seconds. The rules are the same for getting from base to base as the rules for stacking baseballs in boxes.
The number of feet you’ve run is the speed in feet per second multiplied by the number of seconds it takes. Figure 2 shows the result when a runner goes from first to second during a slow home run trot of 10 feet per second for nine seconds. It looks just like the stack of 90 baseballs.

Instead of stacking imaginary boxes labeled in feet, you can just draw the graph of speed vs. time. The space under the curve will tell you the distance you’ve gone. This is shown in figure 3 for the 10 feet per second trot that takes nine seconds. Each small box is one foot per second tall and one second wide, so it represents one foot of the distance.
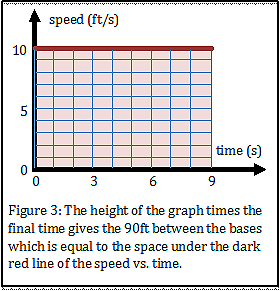
I know, you are used to thinking of space as area, which comes in square feet instead of just feet. However, if you can just get over it for a minute, you’ll see the how useful this type of thinking can be. Let’s expand on the idea and move from a trot between the bags to a bit more realistic steal of second base.
The maximum speed of a runner might be around 30 feet per second, so the graph of speed vs. time would look like Figure 4. Now, each small box is three feet per second tall and one-third of a second wide. Multiplying these numbers means each box still represents one foot of distance covered. The red graph needs to go only to three seconds to total 90 feet under the curve.
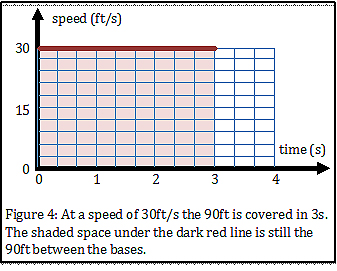
For the purposes for this discussion, let’s break stealing into four parts:
- The leadoff: This is the distance the runner is away from first when he starts his move toward second.
- The jump: Ordinarily, the jump refers to the timing of the start of the dash toward second relative to the motion of the pitcher toward the plate. Here, the jump refers to the time during which the runner is speeding up from rest to top speed.
- The top speed: This is the time during which the runner is moving at his maximum speed.
- The slide: One way or the other, the runner must slow down as he approaches second so he is not tagged out for sliding past the bag.
The leadoff is important because it reduces the distance that must be covered. So, let’s see if you’ve mastered the “space under the graph” idea. What will a leadoff do in regard to the graph of speed vs. time? You got it! The space under the curve is reduced by the amount of the lead. For example, if a runner has a 10-foot lead, the space under the curve only needs to be 80 feet instead of 90 feet. So, the time can be shorter as shown in Figure 5.
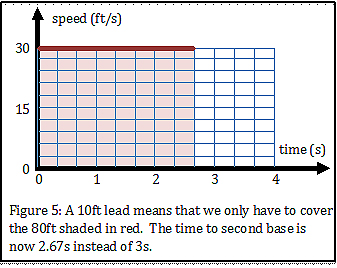
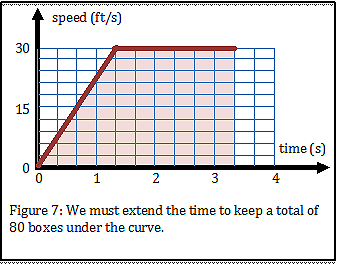
Now, let’s look at the jump. The runner actually begins at rest, not at his top speed. It takes about 1.33 seconds to reach top speed. So, the red graph of the speed vs. time looks like Figure 6. Notice that some of the space that was below the curve is now above the curve.
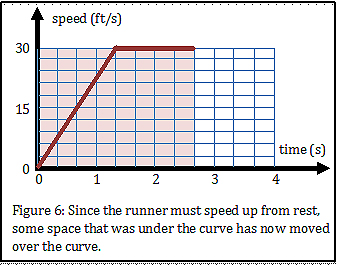
We can’t let that happen. We need the total space under the curve to stay at 80 feet. So, we’ll just figure out how much space we lost and lengthen the time to keep all 80 feet under the red graph. The space we lost was a triangle 1.33 seconds wide and 30 feet per second tall. Remember, the area of a triangle is one-half the width times the height. So, the space we lost was 20 feet. So, we’ll need to go an extra two-thirds of a second to cover the 20 extra boxes. The result is shown in Figure 7. Notice that the time has now grown from 2.67 seconds to 3.33 seconds because we had to take the extra time to speed up.
Well, if it take some time to speed up, then it must also take some time to slow down as the runner nears second base. As we just learned, speeding up costs time, and so does slowing down. This explains why base stealers usually slide past the base. That way, they don’t lose any time by slowing down. Watch for this next time you’re viewing a game. Runners typically slide right past the base and use the base itself to slow down.
Reasoning about the space under the graph can help decide which aspects of base stealing are most important. For example, if a runner has a top speed that is 10 percent higher, we can figure out how many extra boxes (or feet) that would save. Looking at Figure 7, the runner is at top speed for 2.0 seconds and would be moving three feet per second faster. That saves six feet.
Now, consider what happens if he can speed up 10 percent faster. The triangle we lost earlier would only be 1.2 seconds wide rather than 1.33 seconds. Multiplying by half the height of 30 feet per second gives 18 feet rather than the 20 feet from before. So, speeding up more quickly saves two feet. Both the top speed and the rate the runner speeds up make more distance than a 10 percent increase in the leadoff, which only saves only one foot.
At first, it seems surprising that the leadoff makes much less difference than the jump and top speed of the runner. Remember the top speed and ability to accelerate are certainly the most important because only the fastest players can even attempt to steal. For a runner with these prerequisites, a good lead can make a difference. However, you can’t make up for slow foot speed with a big lead. If you would like a more detailed discussion of this model of base stealing you can read this paper.
Well, you should be pretty impressed with yourself if you followed these graphical arguments. Finding the space under a curve is the basis of integral calculus. That’s right, you can now tell your friends you understand integral calculus. Now perhaps you’re wondering why you spent your youth carefully avoiding math class.

Interesting point about avoiding math class. I always felt that if high school math teachers used used sports as a teaching tool, students would be more able to understand a subject that intimidates them.
There are also 90 feet between bases no matter how fast you travel from one to the next.
A nice, if very simplified, explanation of the physics of stealing, but you would suck at baseball trivia. The bases are laid out on a 90 foot square, but home plate, first and third are entirely on the inside of that square and second base has the squares sides intersecting at its center. Since the base itself is 15″ square, that shortens the distance from first to second by 22.5″ making the distance between the bases 88 feet 1.5 inches. If you don’t think that those 22.5 inches makes a big difference between the success or failure of a stolen base attempt you need to spend some more time looking at how close the outcomes often are.
At 30ft/s the 22.5 inches makes 0.063s difference – so, even though I forgot about this geometry, at least I can calculate its importance! Now, I just need to figure out how to stack 88.13 boxed baseballs…
So if a player’s top speed and jump are more important than the size of the lead, I would like to see a player at first drop into a stance using first as a sprinter’s starting blocks. Many good base stealers have track and field backgrounds. I would be interested in whether or not the base stealer would be more successful.
I believe the jump isn’t just the minimization of time to top speed, but also the extra time “stolen” by taking off as soon as possible after the pitcher has committed to throwing to the plate.
A significant number of pitchers are so bad at holding baserunners on that it seems that the baserunner gets half a second or more – the full windup – as their “jump”.
And if this is true, then such time is far more important than speed. Or in other words, the base gets stolen on the pitcher, not the catcher…