The Physics of Falling Baseballs

There are a lot of physics behind making a catch like this. (via Keith Allison)
It breaks your heart. It is designed to break your heart. The game begins in the spring, when everything else begins again, and it blossoms in the summer, filling the afternoons and evenings, and then as soon as the chill rains come, it stops and leaves you to face the fall all alone. You count on it, rely on it to buffer the passage of time, to keep the memory of sunshine and high skies alive, and then just when the days are all twilight, when you need it most, it stops.”
― A. Bartlett Giamatti, Take Time For Paradise: Americans And Their Games
Here I am once again staring out the window. Sometimes it drizzles and the droplets fall as if in slow motion. Other times it pours as large drops scream toward the ground. To cheer myself I sometimes imagine baseballs falling as rain.
Gabby Street must have imagined a similar scenario. Charles Evard Street had an intriguing major league career which began with the Cincinnati Reds in 1904. He was “lent” to the Boston Beaneaters midseason in 1905. Apparently, he sat out ’06 and ’07 then played four years with the Washington Senators. He ended his journeyman career with the New York Highlanders in 1912.
Gabby’s fame came from two events. He managed the 1931 Cardinals to the World Series championship and, in 1908 while with the Senators, became the first person to catch a ball dropped from the top of the Washington Monument. This, like nearly all baseball legends, is debatable. Nonetheless, the actual ball that was used seems to be available for sale.
Gabby Street spent a good deal of time that season catching Hall of Fame flamethrower Walter Johnson. So it could be said that he was well prepared to catch a ball hurling at high speed, but just how fast will a dropped ball be going?
Let’s start thinking about falling objects on the moon where there is gravity, but no air. It would be pretty easy to find the speed of any falling object because they all speed up at the same rate – 3.6 mph every second. This experiment was actually done on the moon with a hammer and a feather by Apollo 15 Commander David Scott.
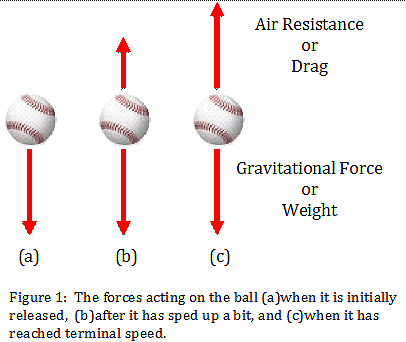
On Earth, things are a bit more complicated. As a ball or raindrop falls it feels two forces; the gravitational force often called “weight” and the air resistance usually described as “drag.” These two forces are shown in figure 1 at three different times during the fall. The weight alone would cause a falling object to speed up by 22 mph every second about six times the rate on the moon.
However, the drag keeps the speed from growing so rapidly. Drag sounds like it is a bad thing, but imagine a world without it. If only gravity acted, then a raindrop falling from 10,000 feet would hit the ground at more than 500 mph! Getting hit by a raindrop would be about the same as getting hit by a rifle bullet. It is the air drag that allows the rain to fall gently.
The drag grows as the speed of the falling object increases. When the ball is first released, it is barely moving and feels almost no drag (figure 1a). After the ball has fallen a bit and acquired some speed there is some drag opposite the motion (figure 1b). Eventually, the ball is moving so rapidly the drag force becomes equal in size to the weight (figure 1c). At this speed – the “terminal speed” – the ball feels no net force and cannot speed up any more.
The drag force not only grows as the speed increases, it depends upon the mass and shape of the moving object in very subtle ways. If you want to learn more about the details of the drag you might start at Wikipedia. If you are more mathematically inclined you could examine this paper. In any case, I worked out the curves for the speed versus the distance fallen for raindrops and a baseball as shown in figure 2.
A small droplet in a drizzle (purple) reaches its terminal speed of 8 mph after falling just a couple of feet. A larger drop from a downpour (green) has around twice the terminal speed, 17 mph, after falling roughly 30 feet. After falling 40 feet a baseball (blue) is falling at almost the same speed as it would if there were no drag (red) on it at all.

During these 40 feet, the droplet is mostly in the situation of figure 1c where the weight is completely balanced by the drag so it can’t speed up any more. The larger drop is mostly in the intermediate condition of figure 1b where it can still speed up a bit because the drag has not gotten as large as the weight. The baseball is in the state of figure 1a where the gravitational force is much larger than the drag.
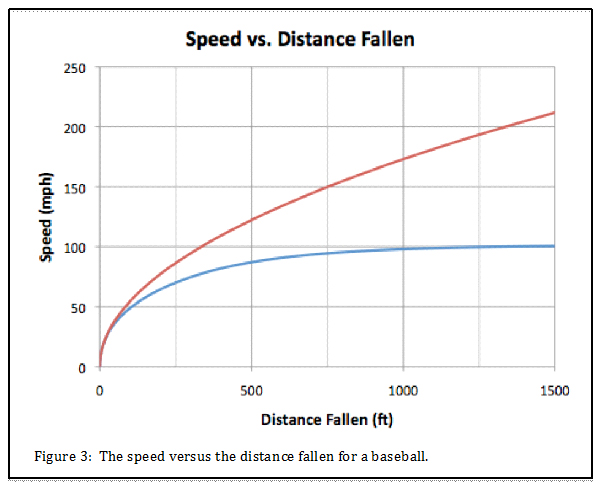
So, the baseball must fall farther to reach its terminal velocity. Figure 3 shows the fall of a baseball over a 1,500-foot distance. Consistent with figure 2, the ball’s speed is essentially unchanged by the drag over the first 40 feet. However, by the time the ball has fallen 250 feet drag is clearly slowing it down.
Back to Gabby Street. The Washington Monument is 555 feet tall. Of course the windows are a bit below. Looking at figure 3, it appears that the ball was traveling about 89 mph when it reached the ground. So, in terms of speed, this was most likely slower than the typical Johnson fastball Gabby had been catching all season.
The invention of airships added additional opportunities to catch baseballs dropped from great heights. In 1926 even the mighty Babe Ruth caught a ball dropped from a plane which, according to The New York Times, was at a reported altitude of 300 feet. According to figure 3, the ball was moving at only about 75 mph.
In 1930, Cubs catcher Gabby Hartnett (does every catcher before World War II have the nickname Gabby?) caught a ball dropped from a blimp reportedly at an altitude of 800 feet (again debatable). What is not up to speculation is the physics of figure 3. After an 800 foot drop the ball would be going about 95.5mph.
More recently, Zach Hample, whose website claims he “snagged 7,806 baseballs at 51 different major league stadiums since 1990,” made two attempts to catch a ball dropped from over 1,000 feet. The first ended when the wind came up, but the second effort was successful. He blogged extensively about it beginning in 2012.
Let’s take this opportunity to see if you have mastered the physics of the dropped ball. Our graphs tell us that after falling 40 feet the ball will be moving 33 mph. After 300 feet the speed is about 75 mph, for 550 feet we get 89 mph, and at 800 feet it’s 95.5 mph. What’s your guess for a 1,000-foot drop? Does your guess agree with the graph? The calculation gives 98.1 mph.
You can definitely see the drag lets the ball speed up rapidly when it is moving slowly. However, it speeds up more slowly as the speed increases leading to a terminal speed. In fact, the ball at 1,000 feet still has a few mph to go to reach terminal speed. Judging by the graph it would need to drop a bit closer to 1,500 feet.
Well, at least I had something else to think about for while. But now it’s back to no baseball and the rain. What a drag…

Greetings,
My name’s Bruno Quaresma and I’m contacting you because I’d like to reach the person in charge of the advertising in your site. Could you please send me the email address for that person? My company is really interested in running some ads and would like to discuss the details in case you are interested.
Thanks in advance.
Merry Christmas!
Bruno Quaresma
brunoquaresmaads@gmail.com
I was hoping this would be more about balls hit in a game. Like how high is the average infield fly, and what’s its speed as it lands? How about home runs? How fast are they going when the fan in the bleacher barehands it?
Thanks for reminding me about Gabby Street. I remember reading about that when I was about 12.
Thanks for the ideas….I’ll see what I can do over the next month or so…..
Rotation will matter since seams are so important in baseball dynamics. Have your models included some range of rotation rates to investigate the range of possible terminal velocities?
As Neal mentioned rotation is an important factor… the math gets much more complicated but would be curious to hear your thoughts.
Also in your anecdote of the ball being dropped from a plane, you only considered the vertical vector of velocity — presumably the plane had enough airspeed to stay aloft, and any object dropped from the plane (rather than thrown backward) would have the same horizontal velocity vector, and the total speed (sum of the horizontal and vertical vectors) would be higher than you estimated.
Without thinking too much about it, the spin will cause sideways deflections. The downward speed won’t be changed much, since as I understand it, there is little evidence that the drag varies strongly with the spin.
The “A ring” catwalk at Tropicana Field is very rarely struck, and is 181-194 feet above the surface. So you could say that pop ups top out just below 200 feet.
Thanks for the shout-out. Catching a baseball dropped from a helicopter 1,050 feet high was BY FAR the most fun, bizarre, and surreal physical challenge of my life. And yeah, it did feel like the ball was falling pretty fast.
“does every catcher before World War II have the nickname Gabby?”
Lots of chatter coming from behind the plate would be my guess: Positioning fielders, reminding everyone of the count/outs, ragging on the batter, yapping at both dugouts, that sort of thing.