The Physics of Going From First to Third

Euclid, the Greek mathematician known as the “Father of Geometry,” was the first to establish the rules for laying out a ball diamond. Yeah, I know baseball wasn’t even invented yet. Nonetheless, he built the mathematics to describe the behavior of lines and points on flat planes.

You see Euclid’s work whenever you marvel at the exact right angle created by the foul lines as they intersect precisely at the back point of home plate. The perfection of the square with bases at each corner is another jewel of his theorems.

While Euclid never got around to proving a straight line is the shortest distance between two points, it certainly seems reasonable enough. When the runners go “station-to-station” a straight line is certainly their best bet. However, when trying to collect two or more bases at a time, straight lines are not the best choice.

Let’s understand this by looking at a runner on first trying to go to third base on a single to right field. The defense usually has its outfielder with the best arm in right, so the key for the runner is to minimize the time needed to touch second and move on to third.

Running in a straight line from first to second would require the runner to slow down as he approaches the bag so he can make the turn toward third. Then it would take a bit for him to speed up again. The slowing down and speeding up costs valuable time.

Now you see why ballplayers actually swing out in a wide arc as they run between first and second. They can then maintain their speed as they “round” second and head for third.

Figure 2 is a sketch of the graph of the time to second base versus the length of the path the runner follows. The straight-line path is the shortest but requires the runner to slow down and speed up, which increases the time. On the other extreme, making a very wide arc increases the path distance, thereby increasing the time. Somewhere in between there must be an optimal arc for minimum time.

Mathematicians have devised a solution to this problem. They claim the best path arcs 18.5 feet away from the baseline. The distance along this path is just under 100 feet as compared to the 90 foot straight-line distance between the bases. I’m pretty sure I’ve never seen a runner take a turn that wide.

In any case, that solution is based purely on mathematics, not physics. The question is, why don’t runners usually follow the 18.5 foot arc? To get an answer, we’ll need to think about the forces on a runner moving on a curved path. Understand that I am not talking about the forces along the motion of the runner because at top speed they roughly cancel out. That is why they are no longer speeding up.

Instead, we need to look at the forces that keep objects moving along a circular arc as shown in Figure 3. Earth provides the gravitational force (shown in red) on the moon that acts toward the center of the moon’s circular orbit. Without this force, the moon would fly off into space in a straight line along its current velocity (shown in blue).

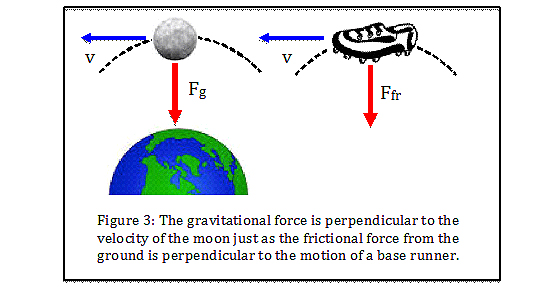
In a similar way, the ground provides a frictional force on the runner’s shoe that acts toward the center of the circular path of the runner. Again, if this force were absent the runner would just keep moving in a straight line along his current velocity. It is the friction between shoe and the ground that keeps the runner turning along the arc.

Vocabulary lesson: these forces acting toward the center causing objects to travel along a circle are called “centripetal forces.” Homework: use the term “centripetal force” in a casual conversation!

Figure 4 shows the foot of runner rounding a bag. If you look very closely, you can see the effect of the frictional force deforming his shoe slightly. To get the bag to exert a large enough frictional force to make the turn, the runner must lean toward the center of his circular arc. The same thing happens when you lean in to make a turn on your bike. Also, roadways are banked to help your car lean into a turn.

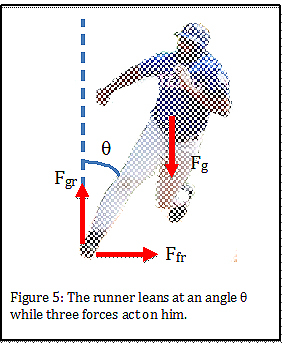Figure 5 shows the forces that act on the runner. Gravity (F_g) pulls him downward, the ground (F_gr) pushes upward, and the friction (F_fr) acting along the ground keeps him moving along the arc. The frictional force becomes larger as the angle he makes with the vertical increases.

Now we can better understand the real question: Can the runner follow the 18.5 foot arc without having to lean in so much that he loses his footing and goes down in a heap? Using the Laws of Physics we can graph the angle versus the speed of the runner along such an arc. The result is shown Figure 6.

The graph shows if you walked this path, the angle you need to lean is zero. You wouldn’t need to lean at all. However, the faster you run the more you need to lean inward.

Michael Clair wrote an article listing the fastest speeds around the bases in 2014. His winner was Dee Gordon, who circumnavigated the bases in a scorching 13.89 seconds on what was ruled a triple and an error. This gives an average speed of 17.7 mph which implies his top speed was probably around 20 mph.

If Gordon was following the 18.5 foot arc, the graph indicates he would have had to be leaning in about 23˚. It is very hard to tell in the replay exactly where he was and what angle he had. However, my gut tells me that he would have crashed and burned had he taken a path that required him to lean in that much.

While there seems to be no definitive evidence to overturn the mathematicians’ claim that the best arc is 18.5 feet from the baseline, at least physics explains why runners need to lean into the turns as they round the bases.

So, in summary, let’s leave the math to Euclid and the mathematicians. After all, the purely mathematical approach is incomplete without using the physics to find the optimal path from first to third. Once again, we see that some of the best experimental physicists on the planet are the ballplayers themselves. They seem to know instinctively the best path to take.