The Pyramid Rating System: JAWS on a Career Scale

Would Juan Pierre’s career have been viewed differently if he played in a different era? (via Keith Allison)
Editor’s Note: This article was initially presented as a poster at the SABR 45 convention in Chicago in June 2015.
With WAR, Wins Shares, Grey Ink, Black Ink, JAWS, VORP and hundreds of other lesser known metrics that seek to evaluate player value on not just a yearly scale but a career one as well, why create yet another one?
But what if for all of these years we’ve been taking the wrong approach to this problem? Nearly every approach I’ve seen toward evaluating players on a career scale is the same approach we use to rate them on a season scale. Come up with a statistic, sum or average it, and whoever has the better number is the better player. But nothing ever seems to hit that sweet spot for how to fairly evaluate a player who played for many seasons, but was never particularly dominant in any of them, against someone who didn’t play for nearly as long, but was very dominant at his peak. The problem, I believe, isn’t the lack of a statistic, but the lack of a method on how to evaluate players on a career scale. The Pyramid Rating system could be an answer to that problem.
How is it different? Instead of relying on traditional methods of mathematics, the Pyramid Rating system is based on the concept of Iteration, one of the most underutilized concepts in sabermetrics — at least in my estimation. It is so underused that when I started doing it I thought I had created a new mathematical concept. Iteration is the act of repeating a process with the aim of approaching a desired result. As it relates to the Pyramid Rating system, it’s the idea that we can build a mathematical model that teaches itself based on a series of assumptions and becomes more accurate the more frequently the model is used. The assumptions are as follows:
- There is no way of telling if any one player’s dominance is due to his own skill or the lack of skill of others.
- Attributes such as speed, hitting power and fielding ability matter only as much as the season or league values them.
- It is impossible to say with much degree of certainty how a player in 1922 would fare in 2012 and vice versa.
- The talent curve and pyramid curve are one and the same.
- The difference in skill level between the best and the second-best player in any year is always far greater than the worst and the second-worst player, regardless of the difference in overall production.
- The rating system is proportional to the number of major league players, meaning 2013 is likely to have more players rated as being great than is 1913.
- The average player in any one season is graded roughly the same as an average player in any other season.
- Regardless of the size or components of the sample size, the shape of the talent curve never changes.
- Players who produce great seasons are not necessarily great players, but great players produce great seasons.
So what do these assumptions tell us? The first is pretty obvious. We don’t actually know how good any one player is until we compare him to another or series of others. Was Babe Ruth really that great a home run hitter for his era, or was everyone else simply that bad? There’s no way of answering that. All we can say with any degree of accuracy is that Ruth was the dominant home run hitter of his era. It’s in large part because of this that the only way to determine how great a player was is to compare him to his counterparts.
The second point — “Attributes such as speed, hitting power and fielding ability matter only as much as the season or league values them” — I think is of far more importance then people give credit to. People tend to think of baseball as a static game that’s never changed, when in reality it has changed quite a bit over the years. A great bunter may not make much of difference in this day and age, but in the Deadball Era it was essential for scoring runs.
This is directly connected to the third point that “It is impossible to say with much degree of certainty how a player in 1922 would fare in 2012 and vice versa.” It’s probable that Juan Pierre is a perfect example of what would happen if we plucked Ty Cobb and placed him in the modern era. Many of Cobb’s skill sets became less important over the years. Pierre and many others have shown that there is still room for a small ball player in today’s game, but it is unlikely we will ever see a return to the days where players like that dominated the game like they did in Cobb’s time.
Likewise a player like Sam Crawford may have fared much better in a more modern game, but was hampered by the huge dimensions in the parks of his time as well as the less lively baseball. How much better, though, is impossible to say. Therefore, we can accurately compare players only against their counterparts, which means a season-by-season comparison is the only route to take.
To understand the fourth assumption of a pyramid curve — i.e., that the talent curve and pyramid curve are one and the same — we must also introduce the concept of a Pyramid Number. A pyramid number is a figurate number that represents the number of stacked spheres in a pyramid with a square base as seen below:

In case fancy equations aren’t your thing, it can be displayed graphically as well. In the graph, Number (on the x-axis) substitutes for n in the equation above:
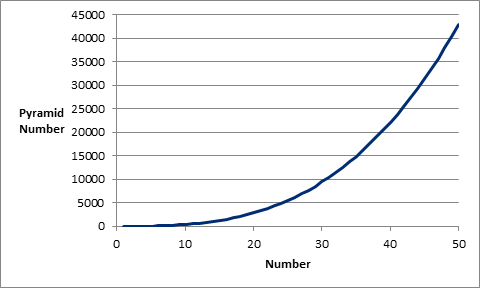
This curve takes the idea of talent being distributed as a pyramid literally. In other words, the curve of the graph will not change no matter how many players are examined. Changing the graph to a rank-based system gives us this:
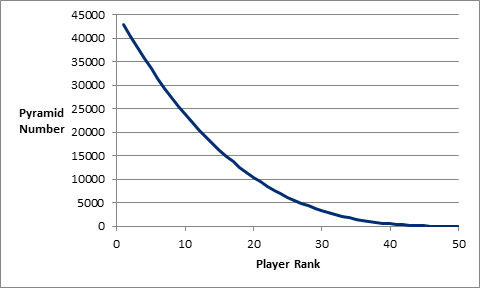
This is the pyramid/talent curve on which every player in major league history falls. As you can see, the dropoff between the player ranked first and the player ranked second is far greater than the dropoff between the 40th ranked player and the 41st. This graph is at the very heart of what this system is about. Using this graph we can easily substitute “Pyramid Number” for “Scout Rating,” as seen below.

This graph mirrors the 2-8 rating system (or 20-80) commonly used by major league scouts. As you can see, the majority of players would rate somewhere between a 2 and 3 on this scale, with only a small handful being given a 7 out of 8 or 8 out of 8 rating. This takes a literal approach to the concept of talent being distributed as a pyramid.
The last assumption — players who produce great seasons are not necessarily great players, but great players produce great seasons” — seems simple on the surface but gets to the point of what a great player truly is. Nobody would argue for Mark Fidrych as a Hall of Famer, but was he a great pitcher? At his peak, Fidrych led his league in ERA and was the rookie of the year. A Hall of Fame quality year no doubt, and if we ranked players solely by their best season, according to this rating system Fidrych would be the 37th best player in major league history. This would put Fidrych ahead of Cy Young, Curt Schilling, Tom Seaver, Christy Mathewson, Warren Spahn and Phil Niekro, among others. Nobody would ever argue that Fidrych was even close to being as good as these players, but take Fidrych at his career peak against those names and it would be a pretty even pitching match-up.
What this means is that the “if I had one game to play and my life depended on it” argument goes only so far. This is the fundamental problem with looking at players purely at their peak value. Doing so will likely give you a very good understanding of how great players were, but without the career stats to go along with it, no player will ever get put into proper perspective.
So how does the Pyramid Rating system work? Players were rated on three sets of criteria, all of which carry equal weigh —endurance, effectiveness and total output. To properly evaluate the standard by which these three criteria are evaluated, I derived the Z-Score for the following stats: Games, plate appearances, WAR/plate appearances and WAR for hitters, and relief appearances, games started, innings pitched, WAR/IP and WAR for pitchers. (A Z-score is the number of standard deviations a number is above the mean.) The equation can be described as seen below:
- z = (x- μ) / σ
Where:
- z = z-score
- x = random variable
- μ = the mean or average
- σ = the standard deviation
The three criteria are broken down as follows:
For hitters:
- Endurance: The Z-Score for plate appearances plus the Z-Score for games played.
- Effectiveness: The Z-Score for WAR/PA * 100 * 2
- Total Output: The Z-Score for WAR * 2
- Note: The reason for the * 2 for Total Output and Effectiveness is to put it on the same scale as Endurance.
For starting pitchers:
- Endurance: (The Z-Score of innings pitched as a starter + The Z-Score of GS) * (number of innings pitched as a starter / number of innings pitched)
- Effectiveness: The Z-Score for WAR * (number of innings pitched as a starter / number of innings pitched) * 100 * 2
- Total Output: The Z-Score for WAR * 2
- Note: The *2 in Effectiveness applies only if the pitcher has appeared in only one role. If he has appeared in both, then the * 2 is added on after the effectiveness scores of both reliever and starter roles have been added together.
- Note: While endurance and effectiveness are split, this number is the same for both starters and relievers.
For relief pitchers:
- Endurance: (The Z-Score of innings pitched as a reliever + The Z-Score of GS) * (number of innings pitched as a reliever / number of innings pitched)
- Effectiveness: The Z-Score for WAR * (number of innings pitched as a reliever / number of innings pitched) * 100 * 2
- Total Output: The Z-Score for WAR * 2
- Note: if a pitcher had no innings pitched as a starter or a reliever his score on any of the three scales was a zero with regard to the role.
The first question some may ask is why WAR? And why the three sets of criteria? I used WAR simply because I found it to be the most readily available statistic of this nature. It could easily be substituted with a similar metric.
The rationale behind the Endurance and Effectiveness criteria is to try to capture parts of player value that I feel WAR overlooks. A player with a 3.0 WAR over 300 plate appearances is more valuable than a player with a 3.0 WAR over 500 plate appearances. Even through their total output is the same, so long as you can find a replacement player with a WAR greater than zero over 200 plate appearances, it is better to have the player with 300 plate appearances.
I also feel there is also value is simply being ready to play, which is the reasoning behind the Endurance criteria, particularly with relief pitchers. To me, a relief pitcher with a 2.0 WAR over 80 innings in 75 games pitched is more valuable than a relief pitcher with a 2.0 WAR over 80 innings in only 50 games pitched. All outs may carry the same amount of meaning in the end, but getting an out in the ninth inning holding onto a one-run lead increases your chances of winning far more than getting an out in the first inning with a one run lead.
This idea tends to get lost a bit with just looking at WAR. Others have pointed this out as well, which has in part led to the creation of stats like Wins Above Average Adjustment and game-entering Leverage Index. Whether this does as good a job of accounting for late game situations is up for debate, but it does get to the larger point of there being value in simply being ready to play.
Looking at games played in terms of evaluating durability is especially problematic when evaluating a player like Whitey Ford, who could easily have pitched several hundred more innings in his career but didn’t simply because he was held back. This does not seek to rectify problems like that, nor does it, although I believe it could be a potential start.
To look at a more detailed example, let’s look at two players. First Roy Campanella in his 1951 season. That year Campanella had 562 plate appearances in 143 games, and 6.7 WAR. So how does that break down on the three criteria scale?
First let’s look at endurance. As mentioned before a player must have had at least 50 plate appearances in a season to qualify. That year, 246 position players had at least that many plate appearances. Of those, the average player came to bat 353 times and played in 96 games. The standard deviation for each of these stats was 204 plate appearances and 40 games.
So, (562-353)/204 + (143-96)/40 equals about 2.2 For any Z-score, the total value of all inputs will zero. Overall, Campanella ranked 47th for endurance. A good ranking for most, but for a catcher it’s outstanding.
The next category is effectiveness. Going back to our equation of WAR/PA * 100, we see that Campanella for that year was 1.18. The average that year was about .2 and the standard deviation was .47. So, ((1.185-.2) / .47) * 2 equals about 4.2. Only Jackie Robinson, Stan Musial and Ralph Kiner (and Jack Merson, a rookie with 52 plate appearances) had a higher effectiveness score that year than Campanella.
The final category is total output. This is simply the Z-Score of WAR * 2. Again, Campanella posted 6.7 WAR that season. The average was 1.25, and the standard deviation was 2.05. Thus, ((6.7 – 1.25) / 2.05) * 2 equals 5.3. Again Campanella has a tremendous showing, with the sixth-best WAR in baseball that year among position players. Adding all of those figures gives Campanella a “Raw Score” of 11.681, sixth-best among position players in baseball that year. We’ll refer back to this number later, when I discuss how to evaluate a player on a career scale.
But where does Campanella fall along the Pyramid Curve for the 1951 season?
To determine his pyramid number we must first ask how many players qualified that year, and where Campanella ranked? We already have the answer to those two questions. Campanella was the sixth-best position player that year out of 246 players.
Referring back to this graph from earlier, we can replace the 0-X with real numbers, since we know there are 246 players, while keeping the curve the same.

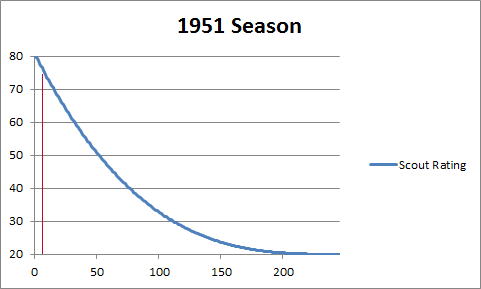
The red line represents roughly where Campanella would fall along this curve. Campanella’s scout rating for the 1951 season was 76.422. On the 2-8 rating scale, Campanella would rate as a 7.6 for that season.
The second player I’d like to present here is one of the more difficult player years to analyze, Tom Gordon’s 1991 season. What makes Gordon particularly difficult is that he was both starter and reliever that year. Gordon started 14 games and relieved in 31. Of the 158 innings Gordon pitched that year, 88.2 came as a starter and 69.1 came as a reliever.
To handle pitchers like this, this system splits Gordon as two different pitchers. First, let’s look at Gordon the starter.
As with hitters for the endurance scale, we evaluate pitchers on two scales, only instead of plate appearances and games played, it’s innings pitched and games started. A player had to pitch at least 25 innings in order to be counted. Eliminating all those players and looking just at anyone who started that year, the average starting pitcher for 1991 threw 112.489 innings and started 18.375 games. The standard deviation for each was 77.855 innings and 11.311 games. So, (((88.6 – 112.489) / 77.855) + ((14 – 18.375) / 11.311)) * 88.6 / 158 = -.389
Next is effectiveness. The average WAR / innings pitched as a starter * number of innings pitched as a starter / number of innings pitched was .576, and the standard deviation was 1.349.
Gordon’s WAR that year was 2.1, so (((2.1 / 88.6) * (88.6 / 158)) * 100 = 1.304.
Based on this we can now calculate the effectiveness score:
((1.304 – .576) / 1.349) * (88.6 / 158) = .303
We now have Tom Gordon’s starter endurance score and starter effectiveness score, but what about his relief score?
Again let’s start with endurance. That year the average relief pitcher appeared in 32.37 games and pitched 44.34 innings. The standard deviation was 24.18 for games and 30.55 for innings pitched. So:
(((69.0 – 44.34) / 30.55) + ((31 – 32.37) / 24.18)) * 69 / 158 = .328
Next is effectiveness. Again the average WAR / innings pitched as a reliever * number of innings pitched as a reliever / number of innings pitched was .579, while the standard deviation was 1.503. It is interesting to note that there was hardly any difference in effectiveness at getting an out between a reliever and a starter in 1991, but the skill level of relievers varied much more drastically then it did for starters. That’s a trend that isn’t unique to 1991.
For Gordon, effectiveness figures as follows:
((2.1 / 69.3) * 100) * 69/ 158 = 1.323
((1.323 – .579) / 1.503) * 69 / 158 = .216 which is Tom Gordon’s effectiveness score as a reliever. Much lower than his starter score of .303 due to the higher standard deviation.
Finally we come to Total Output. The average WAR that year was 1.097 and the standard deviation was 1.806:
((2.1 – 1.097) / 1.806) * 2 = 1.111
Adding up his Endurance scores (-.389 + .328) his Effectiveness scores (.303 +.216) * 2 and his Total Output (1.111) gives us a Raw Score that year of 2.088, which put Gordon 140th overall out of 339 pitchers.
To see where he falls along the Pyramid Curve we again call on our initial graph.

Replacing X with 339 gives us this.
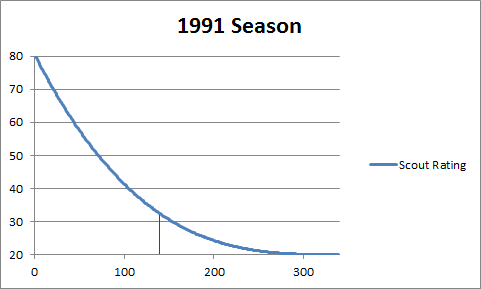
The red line represents Gordon’s approximate spot on the curve. A rank of 140 puts him slightly above average for that season and gives him a scout rating of 32.569.
To compare multiple players and years across different seasons, we use the scout rating for that season and the raw rating associated with it. As before, we rank the raw ratings on a 1-x basis, but this time instead of going season by season, we throw every player’s season in the same pool and rank it 1-x on an all-time basis. We then determine the pyramid number for it, and average it with the scout rating for that season. This ensures that no one season in major league history will be over-represented, while at the same time, making sure that Babe Ruth’s 1923 season ranks ahead of Cal Ripken’s 1983 season even though both were rated the best that year.
Let’s work through an example.
As mentioned earlier, Campanella had a Raw Score of 11.681 and a scout rating of 76.422. Of the 69,959 seasons analyzed, Campanella’s raw score ranking for 1951 ranked 1,259 overall. The ranks of Campanella’s other seasons went as follows:
- 1948: 27,792
- 1949: 5,210
- 1950: 6,992
- 1952: 7,978
- 1953: 1,331
- 1954: 39,431
- 1955: 3,903
- 1956: 32,363
- 1957: 36,230
Plotted along the talent curve, you get this.
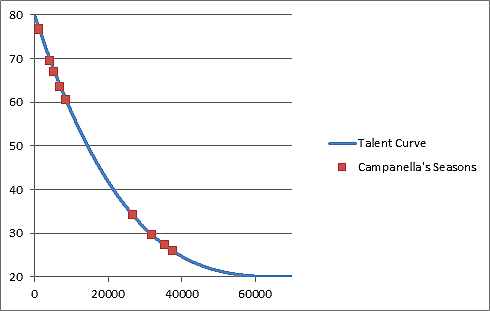
As mentioned before, this alone isn’t enough. We also have to average it out with the scout rank for that season. The average of these two numbers is plotted along the curve to give us our overall Campanella ranking:
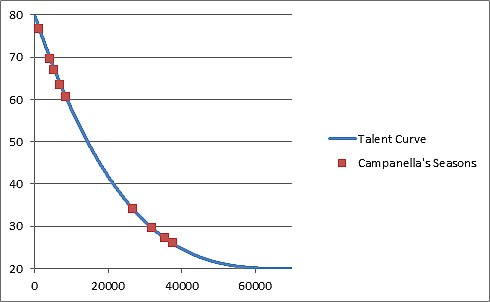
As you may expect, the graph looks very similar, although the averaging does change some things. Despite having a higher Raw rating in 1951, Campanella’s best season winds up being 1953. Including pitchers, Campanella ranked as the 10th-best player in 1951, but in 1953 he ranked ninth.
The final step involves ranking players all-time. To do this, we go back to our concept of the pyramid number.

In this case n would be (the number of seasons ranked – the season rank) +1. Doing this for every Campanella’s seasons would give Campanella a total Pyramid Score of 62.7 trillion. It seems very high, but this would rank Campanella as the 789th greatest player in major league history.
Most would consider that ranking to be far too low. The cause is simply Campanella’s relatively few seasons played. It’s the same reason Cap Anson initially winds up the fourth greatest player of all-time.
It’s the same fundamental issue with using WAR as an all-time ranking. It simply doesn’t do enough to take great seasons into account. But how do we isolate these great seasons?
Whenever we compare one player to another, it’s almost always a head-to-head ranking. When comparing Nolan Ryan to Phil Niekro, it shouldn’t matter what Steve Carlton did. If we removed Steve Carlton’s stats it would alter where Ryan and Niekro would rank and that is precisely what the next step entails.
The player with the lowest Pyramid Score is removed from the player pool and the process described above is repeated.
At first, this does not have much of an effect on the curve. Having the 1,332nd best season out of 69,960 seasons is hardly any different than having the 1,332nd best season out of 69,959 seasons. But as more and more players are removed, how Campanella looks in comparison to the rest of the players begins to change.
As mentioned earlier, this is the initial graph of where Campanella’s seasons stack up against the rest of the players in major league history.
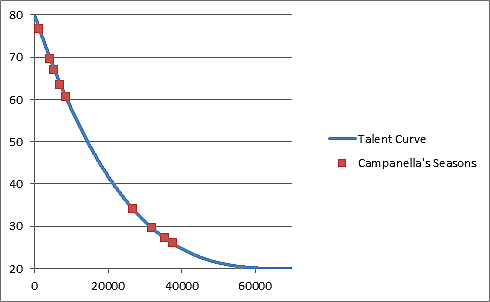
But what if we removed the 10,000 worst players from the pool and replotted Campanella’s seasons along the talent curve based on that?
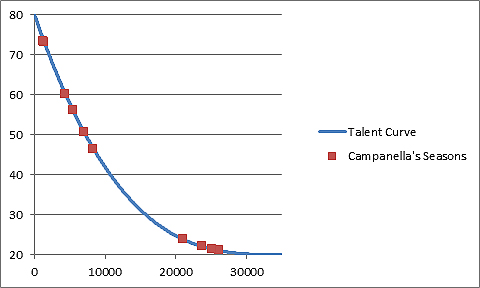
As you can see, all of Campanella’s seasons saw a reduced scout rating, but some more than others.
His 1953 season, which had an initial scout rating of 76.6 now has a rating of 73.4, but his 1952 season — which had an initial scout rating of 60.4 — is now at 46.4.
We can also see how the seasons near or at the top begin to spread out, while the seasons at the bottom begin to bunch up.
If you summed up each player’s total pyramid score at this point, Campanella is now ranked at 607th overall. If we reduce the player pool even more, down to just 2,000, we get this:

You can now see the bunching of seasons at the bottom even more in effect, while the seasons at the top being to spread out even more. The initial scout rating difference between Campanella’s 1951 and 1955 season of 7.1 has more than doubled to 15.8.
We also the see the dynamic of who Roy Campanella was as a player as defined by this system beginning to change. Instead of being a player with two great seasons and four very good ones, he’s starting to turn into someone with two very good seasons and four average ones. That’s because the quality of the players Campanella is being compared to is far greater.
Despite this, Campanella’s overall ranking continues to increase; at this point he is ranked the 560th best player in history. How, and why?
It boils down to his two best seasons — 1951 and 1953. Those two seasons are what’s driving Campanella’s ranking higher and higher. What this suggests is a few things.
For starters, two great seasons can be far more valuable to an organization then six average ones. It also suggests that baseball really has more in common with the NBA in terms of being a superstar-driven sport than we may think. Instead of asking how many wins can this player add to a team, as in Moneyball, a team may instead want to ask itself by what percentage does this player increase our chances of winning the World Series?
What this suggests is that only a small number of players are really capable of increasing your odds. The disproportionate number of Hall of Famers represented in October would seem to further support this argument.
As it relates to Hall of Fame voting, what this seems to conclude is that the only thing we need to be looking at is how many great seasons a player had. Having a great season seems to be the only thing that to really makes a difference in terms of improving a team’s chances at winning the World Series.
Going back to the ranking process: Once only one player remains, the process starts over again, this time with that player removed from the sample size in an effort to keep this as much of a head-to-head comparison as possible. Over time this repetition gives players with many seasons played in the middle a greater edge over those with just a handful of great seasons and not much else.
While the initial goal was to determine the best players in major league history, I believe this system has instead determined the most valuable players in major league history. The difference between the two is due to the ever-changing nature of the game.
This raises the question — should all players be treated the same? In other words, should a good defensive shortstop in the 1920s be seen as a greater player than a modern shortstop possessing the same skills? Because of the greater number of balls hit in the infield in the 1920s, there’s no question he provided more value to the team. But does that inherently make him a better player? I believe it’s a discussion worth having on a far more frequent basis.
While this process was used to try to answer one of the most difficult questions in sabermetrics, and we’ll get into those results more in the future, the process can also be used to find the answers to other questions. For instance, who is the best base stealer in history? It could also be used for other sports and potentially even by companies. It could also serve as a tool for teams to compare talent against injury risk.

Superb.
Nice job, Paul, but I’m pretty sure two of those Campanella graphs are the same.
Not sure which two you are referring to, possibly the comparison between the “Raw Rating” and what Campanella’s stats look like averaged out with his scout rating, but I can assure you they are different.
Yes, I think that’s what I’m referring to. The two graphs that you say look similar, that both refer to Talent curve and Campanella’s seasons. When I look at them, I see two axes with the same labels, same numbers and the same data labels. And the data points themselves appear to be in the exact same place. There doesn’t appear to be any difference to the naked eyel.
In the future, you might want to give each graph a name, or at change the labels between them, if you’re going to be presenting such similar graphs.
Points taken. Thanks for the feedback.
This is very good – but isn’t Campanella the wrong choice for an example? His career was delayed significantly at the outset and cut short a bit at the end, in both cases for reasons taken into account for HOF voters; more important, he was a catcher, so the usual stats don’t apply. C is a key defensive position with exceedingly weak defensive stats, so WAR as it exists is a poor measure. Offensive expectations are limited, and were more limited in the past — Campy hit a lot of HRs and led the league in RBI, highly valued in the ’50s and very unusual for a C. Cs don’t play as many games as other position players, but they’re involved in many more plays.
Campanella just happened to be a random pick. I wanted to pick a batter with a complete career and not someone like Babe Ruth, or Ted Williams who would look good under any metric. Campanella fit the bill on both counts.
What’s most interesting about Campanella as it relates to this is his defensive skills. I would say he’s the best defensive catcher in the NL for his time, yet all-time he doesn’t rank that high all-time on this system. Why? Biggest reason is the lack of stolen bases during that era. It made having a great defensive catcher less valuable then it did say in say 1982.
One look at the range factor will tell you that. Campy was never much above 6 in any season which was good enough to lead the league and in the 70’s and 80’s you can find catchers over 7.
Now does that get held against Campanella or do we try to adjust for that difference? I’m not sure I know the answer to that.
My point we look at these defensive positions as having fixed values in terms of their importance on the field and that’s simply not the case. Positions can and have risen and fallen in value over the years.
“A player with a 3.0 WAR over 300 plate appearances is more valuable than a player with a 3.0 WAR over 500 plate appearances. Even through their total output is the same, so long as you can find a replacement player with a WAR greater than zero over 200 plate appearances, it is better to have the player with 300 plate appearances.”
This appears to be a faulty assumption on your part.
By definition, isn’t the WAR of a replacement player zero? If a team finds itself needing a replacement player with a WAR greater than zero, won’t they be required to spend at least the market rate to acquire such a player?
I think this gives a more in depth analysis of the point I’m trying to make with you eluded to Noah.
http://blog.philbirnbaum.com/2015/03/does-war-undervalue-injured-superstars.html
Modern Ty Cobb would not have been Juan Pierre. More like Rickey Henderson.
I think people are getting too caught up on this.
The point isn’t to say that Ty Cobb wouldn’t be good in this era. The point is that it doesn’t matter what Cobb would be like today, because we don’t ask what players from today would do in his era.
If you want to say there’s better modern day comparisons to Ty Cobb that are out there that’s fine but it has nothing to do with any of the points I’m trying to drive at.
“The second point — “Attributes such as speed, hitting power and fielding ability matter only as much as the season or league values them” ”
Also the fans..if people dont go and have hot dogs and popcorn, sit in the sun, laugh. Without the fans, the tree falling in the forest does not make a sound.
—
The Cobb modern ability stuff is as offensive as Cobb’s personal rep was. Juan Pierre?
The Fidrych stuff applies to so many players. We know this. Tim Lincecum. Felix Hernandez. The Cy Young, Mathewson list is sorta too much.
—
Commenters are right to say dont use Roy Campanella, whose career was cut off suddenly, as a primary example in a study of baseball career arcs. inappropriate.
And then the author trys to play it off. No. No Joe Jackson, either.
—
Graph of defense stats from the 50ies? Yes, Campanella was a good catcher.
This article does not feature any actual pyramids, which are giant stone structures, and not typically linked to curve graphs of baseball fellows.
“Nobody would argue for Mark Fidrych as a Hall of Famer, but was he a great pitcher? At his peak, Fidrych led his league in ERA and was the rookie of the year.”
Maybe you should use a word like “most” in lieu of “Nobody” because there are some fans in Detroit who still consider The Bird to be a HOFer! ERA should not be used to judge a pitcher because it is a TEAM stat. A pitcher is only partially responsible for the number of runs he allows. Also, intentional bases on balls are called by the manager, and if that runner scores, the pitcher is charged. And why are IBBs included in the total number of walks allowed by pitchers? He did not walk the batter. A better stat for evaluating a pitcher is FIP. His FIP was 3.15, while his ERA was 2.34.
BTW, I worked as an extra on the movie “The Sluggers Wife” filmed at Atlanta stadium and met many of the former players used in the film. It was very hot and many of us went shirtless. I still vividly recall how small were Mark’s shoulder blades, and have often wondered if that had anything to do with how long he lasted in the Show…
“A player with a 3.0 WAR over 300 plate appearances is more valuable than a player with a 3.0 WAR over 500 plate appearances.”
This is simply wrong. A player who contributes the same WAR in fewer PAs to a team going to the World Series is more valuable to his team than a player, think Andre Dawson, who contributes the same WAR to a last place team out of the race in May.
“Looking at games played in terms of evaluating durability is especially problematic when evaluating a player like Whitey Ford, who could easily have pitched several hundred more innings in his career but didn’t simply because he was held back.”
We do not know this. I recall reading Casey did not pitch Whitey more often because he did not believe he could handle the workload. If he had pitched more, especially earlier in his career it is possible that he would not have been around long enough to be considered for the HOF.
As for yet another disparaging comment on The Georgia Peach, Ty Cobb, maybe you should read, “Heart Of A Tiger: Growing Up With My Grandfather, Ty Cobb by Herschel Cobb, “Ty Cobb: Safe At Home” by Don Rhodes, and “The Other Ty Cobb” by Tyrus Cobb and Pina Gregorek, and “Ty and The Babe: Baseball’s Fiercest Rivals: A Surprising Friendship and the 1941 Has-Beens Golf Championship” by Tom Stanton, so as not to post something so offensive the next time you post, rube.
Test