Beyond DIPS

The theory of Defense Independent Pitching Statistics can be traced to this famous line by Voros McCracken in Baseball Prospectus 2001:

There is little if any difference among major-league pitchers in their ability to prevent hits on balls hit in the field of play.

This was backed up by year-to-year correlation testing as well as a healthy dose a common sense. Voros then proceeded to classify each event (walk, hit, strikeout, etc.) by whether or not it was influenced by defense. The Three True Outcomes (strikeouts, walks, home runs… and hit batsmen) were considered defense independent, while anything to do with hits were not.

Years later, after much recycling of Voros’ ideas and formulas, the basic theory of DIPS remains. From Tom Tango’s FIP, which only uses the Three True Outcomes and is so simple you can literally calculate it on the back of a napkin, to slightly more complicated formulas like Graham MacAree’s tRA (which uses batted ball numbers) and David Gassko’s Pitching Runs Created, only stats which are deemed independent of defense are considered.

However, DIPS, and all of its decedents, are only designed to model how many runs a pitcher would have given up if defense (and timing) were taken out of the equation. They are not meant to isolate the pitcher’s performance, only to eliminate the defensive performance. In my opinion, this a concept that is often overlooked by many-a-good analysts and dedicated sabermetric disciples out there.

To assume that the only stats that are out of a pitcher’s control are his hit rate on balls in play, otherwise known as BABIP, and the timing of his events is a mistake. Consider all of the factors that go into each pitch that are completely out of a pitcher’s control:

• The batter
• The umpire
• The defense
• The environment (ballpark, wind, etc)

In fact, the only thing a pitcher has complete control of is the inherent attributes of the pitch as it reaches the plate (and even then there are environmental factors to consider). For a long time, we’ve assumed that strikeouts, walks, batted ball numbers, etc. are very much in a pitcher’s control. When you think about that, it is a ludicrous assumption. The batter has at least equal control over the outcome of each pitch as the pitcher does, and the presence of the umpire makes it likely that the pitcher has less than 50 percent control over the outcome of each pitch.

With Pitch f/x data available now for over 1.5 million pitches in the majors since 2007, we can begin to investigate the degree of control that pitchers have over the outcomes of each pitch. My recent research on Jarrod Washburn and A.J. Burnett, suggests, in my opinion, that pitchers have far less control over even their defense-independent stats than we have thought. However, those studies were far from conclusive. Today, I hope to bring a bigger hammer to the table to try to prove my thesis.

OK, it’s more of an allen wrench

First, let’s consider all pitches with the following characteristics:

• From a RHP to a RHH
• Between 91 and 93 MPH
• Between -3 and -7 inches of horizontal spin deflection (movement)
• Between 8 and 12 inches of vertical spin deflection (movement)

Reimagining the MLB Draft
by Jonathan Welter
What if the amateur draft were different?
• On a 2-1 count
• With the previous pitch type being another fastball
• With nobody on base

Since 2007, there have been 536 such pitches thrown in the major leagues that were captured by the Pitch f/x cameras. If you’ve read Josk Kalk’s two part series on the “Anatomy of a league average pitcher” (and if you haven’t, go read it now!), you’ll notice that this is a pretty generic pitch type in terms of it’s attributes (velocity and spin deflection) and it’s environment (count, batter/pitcher hand, baserunners).

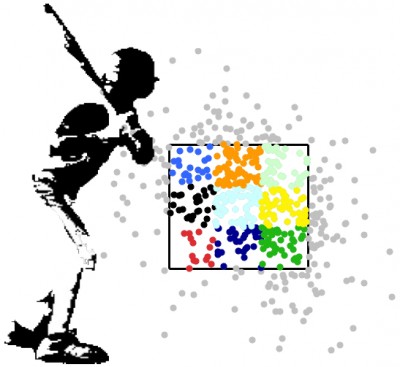
Now let’s break those pitches down by their location in the strikezone. To do that, I first adjusted the vertical height of each pitch in the sample by the top and bottom strikezone estimates for each batter provided by the Gameday operators. I then split the strike zone into nine equal parts. As you can see on the right, while each of the zones are bigger than one might like, they are, at the very least, distinct.

Most importantly, using those zones allows for a comparison of pitches that are pretty homogeneous. They each have similar velocity, movement, environment, and location. There are obviously slight differences, but nothing too significant. Given that, you’d expect the outcomes of each of those pitches to be pretty static if pitchers really had a significant amount of control over the outcomes of each pitch. In other words, you’d expect little variation in what actually happens after the pitch leaves the pitcher’s hand. But is that really the case?

If you take a look at the pitches down and center, the dark blue ones on the batter graph, there were 34 pitches thrown. Three of them were balls, five of them were called strikes, none were swinging strikes, 10 were foul balls, zero were singles, three were doubles, zero were triples, three were home runs and 10 were in play outs. That’s a lot of variation. Just based on random chance, the pitch could either be, say, put in play for an out, or hit for a home run. The difference in value between those two plays is HUGE. Using John Walsh’s Run Values (helpfully cataloged here by THT’s own Harry Pavlidis), the difference between a home run and an out on a 2-1 count is 1.68 runs.

Of course, I cherry picked the one location vector with the most variance, but most of the other ones have a similar amount of variance. If you click that link, you can see the distribution of pitch outcomes based on location. The little white bars represent when the run value of the outcome becomes negative (good for the pitcher). If you check out the distribution of run values by location vector, the picture is pretty amazing:

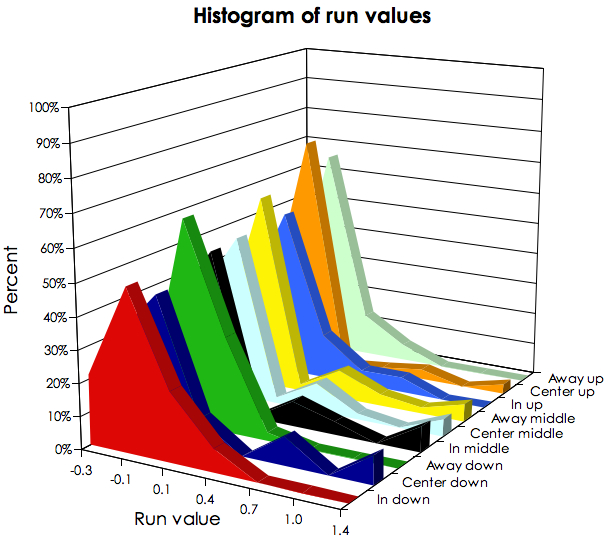
As you can see, while the distributions all peak around -.1 run value, in almost all cases, there is a significant chance that the outcome of the pitch ends up being much worse, or better, than that for the pitcher. The only location vector with a decent amount of parity is the one for away and down (green). In more than 90 percent of the time, in this subset of pitches, the outcome is either a ball or a non-in play strike.

The problem with the above example is that I’m dealing with a very small subset of pitches, only 40-50 in each location vector. Common sense suggests that the outliers will even out over a large sample size, and similar pitches will have similar outcomes for the most part. However, that’s something we simply can’t investigate further at this point due to the sample size restrictions in creating homogeneous pitch types.

Another thing we can look at is called balls and strikes by the umpire. Josh Kalk, John Walsh and Jonothan Hale have already examined how accurate umpires are in great detail, and found that while they were generally very good, they did make their share of errors. Earlier this year, I took a look at how those errors were distributed over individual pitches, and found that there was a lot variance.

So what now?

This study is hardly conclusive, but I think that, along with my previous two articles on Washburn and Burnett, it does show that pitchers have a lot less control over the outcomes of pitches than previously believed. Even stats that aren’t affected by defense at all are heavily affected by other factors, such as the batter and umpire. The next frontier of pitching stats, in my opinion, should be exploring ways to isolate the performance of pitchers from that of those other factors. As of now, the only way I can think of doing that is by using Pitch f/x data, and to look at the inherent qualities of each pitch and not care about the actual outcome. While any kind of comprehensive Pitch f/x pitching metric is far from being ready, I’d like to explore some possible ways in which one could be created.

Binning

This involves identifying the key characteristics of each pitch, and creating a number of unique combination of such pitches. For example, you could look at all pitches thrown from a RHP to a RHH in a certain count with a given range of velocity, spin deflection and location coordinates, and figure out the average run value of such pitches. Repeat that for every combination of pitch attributes there are. This is similar to the methodology behind UZR, and is a very “clean” process. With enough data, this, in my opinion, would be an excellent way to develop a Pitch f/x based pitching metric.

The problem is that we simply don’t have enough data right now. There are simply too many combination’s of pitch attributes (count, batter hand, pitcher hand, speed, movement, location, previous pitch type) to get reliable samples for most of the bins. That leads to wacky things like, with all else being equal, a 91-93 MPH fastball being more effective than a 93-95 MPH fastball. Obviously that can’t be true, and it serves to show that we simply don’t have enough data to do comprehensive binning.

Regression

This is a good method to use if you have sample size issues in some bins – which we do. Regression looks at the overall estimated relationship of datapoints, rather than each individual set of points. Regression usually does a pretty good job of neutralizing sample size oddities. Some very good work on regression and run values has been done Jeremy Greenhouse and Chris Moore at Baseball Analysts.

Jeremy used what’s known as a LOESS regression to estimate the expected run value of a given pitch given its velocity and movement. This is a very powerful technique, but it has its flaws as well. For one, the variables in Pitch f/x are often so random, following no discernible pattern, that a regression technique might not be able to give enough of a range in value. Furthermore, LOESS does not produce a closed form equation, making it very hard to apply to all pitchers. And like with the binning method, sample size oddities can skew the results of given pitch types – especially for lefty-on-lefty matchups, pitchers with strange release points and less populated counts. I’m not sure if LOESS is strong enough to compensate for all of that, but my inclination is that it is not.

Other problems

Even if we had enough data for the binning method or enough flexibility for the regression method, there would still be massive problems in creating a Pitch f/x based pitching metric. For one, those methods would simply estimate the value of each pitch, not of the eventual outcome of each at-bat. Obviously, the way in which pitches are sequenced together has a huge effect on the eventual outcome of at-bats, and to treat each pitch as its own separate and independent entity would be a mistake. Furthermore, there are aspects of pitching that aren’t quantified by Pitch f/x data. Deception, which involves a player’s windup, his time to the plate, his glove, etc. are not going to be captured by a Pitch f/x based metric, and potentially have a big impact on the expected value of a pitch.

Conclusion

I feel as though this article has raised more questions that it has answered. If you accept my thesis that pitchers only have limited control over what happens after the pitch leaves their hand and the experiments that I set up to prove that, you should accept that one of the biggest potential advancements in sabermetrics will be a Pitch f/x based pitching stat. The question is whether or not we will have to capacity to develop such a stat, and whether or not the additions over current DIPS metrics (the fact that it won’t rely on outcomes which are influenced by the batter and the umpire) will outweigh the subtractions (will have a tough time handling sequencing of pitches and other pitch attributes that aren’t captured by Pitch f/x).

I feel it will be a worthwhile endeavor for one to go about creating a Pitch f/x based pitching metric, and while I am no closer to creating one than when I started this article, I hope that it will be an important part of new research in 2010.

References & Resources
A great article written by Mike Fast in the beginning of 2009 suggested that pitchers have more control over the outcomes of balls in play than DIPS gave them credit for. He also used Pitch f/x data, but looked primarily at where the balls were put in play. That research doesn’t necessarily contradict my own; however, it’s obviously related, and Mike has a great summary of the DIPS timeline at the bottom of the post.

I’m still thinking of experiments like in the “OK, so it’s more of an allen wrench” section to set up to try to show how much variance is expected in the outcomes of pitches. I’ve been racking my brains for a couple of weeks, but I can’t really think of another way to approach that problem. If anyone has suggestions, feel free to sound off in the comments section or email me, and I’ll try to investigate them.

Something else that I feel I should have mentioned in the article, but don’t really have a place to put it, is that a Pitch f/x based metric could be amazingly useful for rookies or pitchers coming back from injuries. Given that a Pitch f/x based metric would take out almost all of the noise associated with traditional stats, the sample size requirements for predicting future performance would likely be far less than for the current stats out there.