Confessions of a DIPS apostate
 |
| Troy Percival considers how he has allowed a yummy .266 BACON. (Icon/SMI) |
With apologies to Mary Anne Sadlier for the title, I’d like to share some of my recent thoughts and findings related to the ability of major league pitchers to control the opposing hitters’ batting average and home run rate on batted balls. I have spent the better part of the past year wrestling with the Defense Independent Pitching Statistics (DIPS) concepts postulated by Voros McCracken beginning in 1999 and published on Baseball Prospectus in 2001. McCracken posited that pitchers have little control over the result of batted balls other than home runs.
There is little if any difference among major-league pitchers in their ability to prevent hits on balls hit in the field of play.
McCracken expanded and refined his own work, and many others have added to it since then. These findings have provoked much controversy but have come to basically be accepted at least throughout sabermetric circles. If you are interested in reading further about the existing research in this field, there is a list of some of the important articles in the References section at the end of this article. In fact, I’d encourage you to take some time and follow the links in the Reference section. You’ll probably learn more by doing that than you will by reading what I have to say. I’ll have a cup of hot chocolate and join you back here in a few minutes.
Home run rates and BABIP on fly balls
I am more interested in investigating whether pitchers have any quantifiable way of consistently generating weak contact on batted balls than I am in improving or changing DIPS. DIPS theory asserts that they do not, or at the very least, if they do, that ability is captured within the the DIPS statistics. I’m not going to try to prove or disprove that, but I do want to investigate how weak contact and solid contact on batted balls come about.
The more I have learned about pitchers through the lens of PITCHf/x, the less I find it squaring with the (now) widely-held DIPS theory. The holy grail of PITCHf/x research is answering how and why pitchers are effective, but it is, to my mind at least, a quest largely unfulfilled despite some great work by analysts such as Joe P. Sheehan, John Walsh, and Josh Kalk. Particularly elusive is an answer to the question of what makes any one specific pitcher effective or ineffective.
I do not claim to have found the chalice, but I present some of my findings here in order to get feedback and stimulate further discussion. The first of these findings is the subject of this article, that the direction of an outfield fly ball has a major impact on home run rates and BABIP on that fly ball.
Using the MLB Gameday data from 2007 and 2008, I classified all fly balls by whether they were hit to the pull field, center field, or the opposite field. (For right-handed hitters, the pull field is left field; for left-handed hitters, the pull field is right field.) Batters get much better results when they pull the ball. Here I report numbers for batting average on contact (BACON–thanks for the great acronym, Colin!), slugging average on contact (SLGCON), and the more traditional numbers for batting average and slugging average on balls in park (BABIP and SLGBIP).
Direction Fly Balls BACON SLGCON BABIP SLGBIP 1B% 2B% 3B% HR% Avg.Distance Pull 20440 0.452 1.467 0.218 0.384 4.6% 9.6% 1.0% 30.0% 304 ft. Center 30809 0.217 0.498 0.171 0.293 6.3% 8.2% 1.7% 5.5% 295 ft. Opposite 27249 0.182 0.378 0.153 0.248 6.4% 7.6% 0.8% 3.4% 262 ft.
Batters average a base and a half every time they make contact and pull a fly ball! The pull field is definitely the power field. On the other hand, fly balls hit to center field or the opposite field do not fare nearly as well.
If we further subdivide the field into wedges of five degrees each, we can see these effects more clearly.
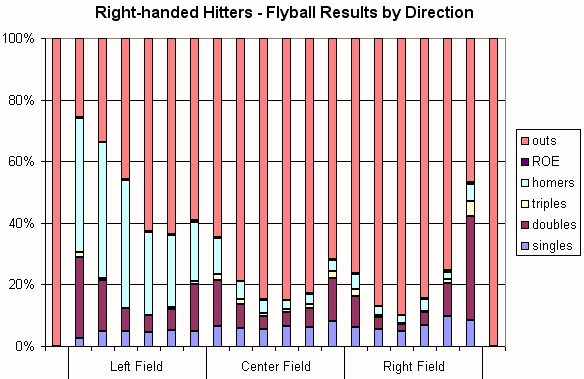
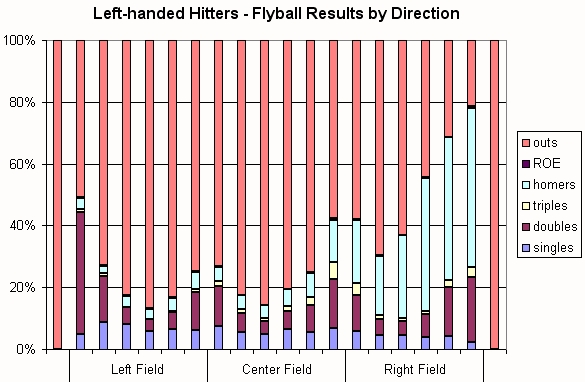
You can see dips in the percentage of hits around the typical position for each of the three outfielders. The hit rate to the pull field is much higher, mostly due to the increase in home runs. The only wedge with a high hit rate to the opposite field is the one adjacent to the foul line where hitters can poke doubles out of the reach of fielders. Even toward the opposite field gap, right-handed hitters only managed a .283 batting average on fly balls, and left-handed hitters a .269 average.
Let’s focus on the home runs for a moment.

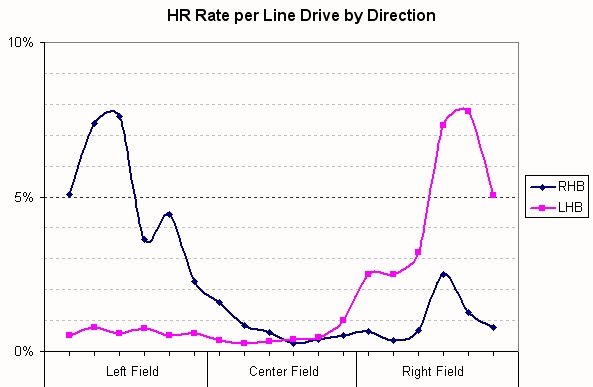
The more a batter pulls the ball, the more likely he is to hit a home run, as long as the ball stays fair. The outfield fences are farthest from home plate in center field and closer as we near the lines, and this clearly has some effect to center and the pull field. However, in the opposite field we don’t see hitters take advantage of the closer fences until we get right next to the line, where they can tuck an extra 2-3 percent of their flyballs in that direction around the foul pole for home run. Why is this? Aren’t the power alleys supposed to be to left center for a right-handed batter and to right center for a left-handed batter?
In The Physics of Baseball, Robert Adair discusses the batter’s swing.
The batter in the diagram is assumed to have swung in such a manner as to drive a ball to center field as far as he can. If this right-handed batter should miscalculate the velocity of the pitch and hit the ball 0.005 seconds early, and to right field, he would hit the ball before maximum bat velocity was realized and generally not hit the ball quite as hard. Since the loss of energy after the maximum is reached is usually small, if he swings too quickly, by 0.005 seconds, he will lose little power in driving the ball to left field.
A pull hitter swings so as to maximize the bat velocity a little later in the swing. In general, the pull hitter has more time and distance to apply force to the bat and can therefore transfer a little more energy to the bat and hit the ball a little harder.
So Adair explains why hitters are generally able to drive the ball harder to the pull field than to the opposite field. But there is another piece to the home run puzzle and the question of power alleys, to which we will return after a short detour to discuss the quality of the data itself.
Data integrity
The MLB Advanced Media fielding data which I used for this study has some issues, some unique and some common with proprietary data from Baseball Info Solutions (BIS) and STATS. MLBAM data contains the location that the ball was fielded rather than the location where the ball first hit the ground. Ideally, we’d like to know both locations. Having only the fielding location could be a problem, particularly in the outfield, for constructing a zone-based fielding metric. However, for the purposes of this article we are generally concerned with the vector along which the ball was hit rather than the landing distance, so we are largely unaffected by this feature of the MLBAM data.
More problematic is the fact that prior to 2008, not all ballparks used the same origin for the coordinate system; moreover, those earlier ballpark-specific coordinate systems are no longer available on mlb.com and are not easy to determine accurately from the data set itself. Peter Jensen is an expert on this topic, and I have word that he will be publishing something on it in the near future. After a few abortive attempts, I decided not to make any ballpark coordinate system corrections to the data I have presented here. I believe in general that the effects from coordinate systems are small compared to the overall batter- and pitcher-related effects I discuss, but for a specific batter or pitcher in an affected ballpark, I would not be as sanguine about relying on uncorrected data.
One concern in common to all the fielding data sources is the classification between fly balls and line drives, something recorded by subjective decision of an observer. This is true for the MLBAM data, and, as far as I am aware, the BIS and STATS data, too. BIS includes an intermediate category called fliners, further broken down in fly fliners and liner fliners, as an attempt to address this problem. At the boundaries between these categories, however, a similar concern about subjectivity of the classification applies. There has been speculation that, given similar trajectories, the observer might be more likely to classify a batted ball as a fly ball if it were caught and a line drive if it fell for a hit. Can we see this effect in the MLBAM data?

Oddly enough, we see both fly balls and line drives peaking around the typical positions of the three outfielders and dipping in the gaps and along the lines. I can’t think of any reason for balls in the air to preferentially group around those three vectors, so I assume that must be a scoring bias. Accurately marking the location of a ball fielded in the middle of a vast outfield expanse free of landmarks is a challenge, and the MLB stringer may tend to mark the fielding location closer toward the typical fielding position of whichever outfielder fielded the ball. I don’t know whether BIS and STATS data suffer from a similar bias.
In attempt to remove the aforementioned bias and still approach an answer to our question about scorer line drive/fly ball classification bias, I removed line drives caught on the infield and then computed outfield line drives as a fraction of all outfield air balls (line drives plus fly balls). In the resulting graph, I believe we can detect some evidence of scorer bias in the classification of outfield air balls.
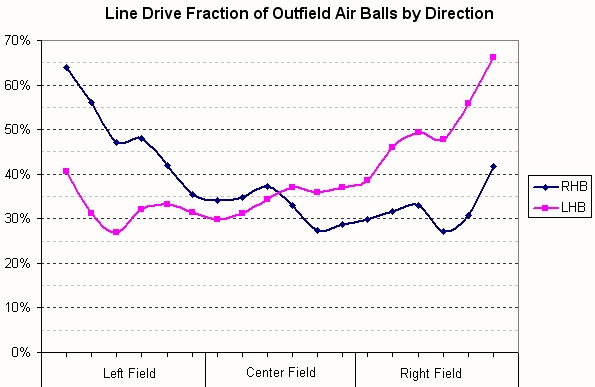
There is an overall trend toward a higher line drive percentage as the batted ball direction moves toward the hitter’s pull field. This presumably is a real effect. Overlaying this trend, however, we can detect a bump in the line drive fraction near each of the three outfield positions. Surprisingly, this leads to opposite conclusion from what I and others originally suspected. Scorers tend to a label an outfield batted ball more often as a line drive if it is caught and as a fly ball if it in the gap between outfielders. On the other hand, batted balls near the foul lines tend to be labeled more often as line drives. I’m not sure how to explain this last effect unless there is something about the batted ball being closer to other visual landmarks like the stands and the foul line that make a scorer more likely to classify it as a line drive.
I promised we’d get back to discussing power alleys. According to MLBAM data, home run totals peak somewhere around an angle of 11 degrees in from the foul line of the pull field and fall off by half or more from the peak by the time we reach an angle 20 degrees in from the foul line (roughly straightaway left or right field). My understanding of the power alleys was that they were roughly 30 degrees off the foul line, in left-center field and right-center field. In this data, that appears to be well outside the prime home run zone. Maybe that name came about for some other reason. I don’t believe that scoring bias is playing a role here. Greg Rybarczyk of Hit Tracker graciously confirmed for me that his home run location data agrees with the MLBAM data on the azimuth for peak home run totals.
Home run rates and BABIP on line drives
Having introduced a bit of data on line drives already, I thought you might like to see the batting average and slugging average on line drives divided into pull field, center field, and opposite field, much as we did earlier for fly balls.
Direction Line Drives BACON SLGCON BABIP SLGBIP 1B% 2B% 3B% HR% Avg.Distance Pull 21347 0.753 1.160 0.741 1.015 45.6% 23.7% 1.3% 4.8% 242 ft. Center 17482 0.736 0.906 0.734 0.888 59.3% 12.0% 1.7% 0.6% 246 ft. Opposite 13933 0.697 0.918 0.695 0.893 50.7% 16.7% 1.5% 0.8% 230 ft.
For line drives, the advantage to pulling the ball is still present but significantly muted when compared to the advantage we saw for pulled fly balls. Pulled line drives do result in more doubles and home runs, but this increase in extra base hits comes mostly at the expense of line drive singles. Also, opposite field line drives are not nearly as anemic as their cousins, the opposite field fly balls.
Is pulling the ball a repeatable skill?
All this is well and good and interesting in its own right, but a question naturally arises, namely, can we do anything useful with this data? Is hitting the ball in the air to the pull field a measurable, repeatable skill for batters and pitchers?
We have seen that pitchers as a group allow most of their home runs on fly balls to the pull field. But what about individual pitchers? Does this hold true for every pitcher? I looked at the fly balls allowed by every pitcher in 2007-2008 and charted the home runs they allowed to right-handed batters to each of the three fields.
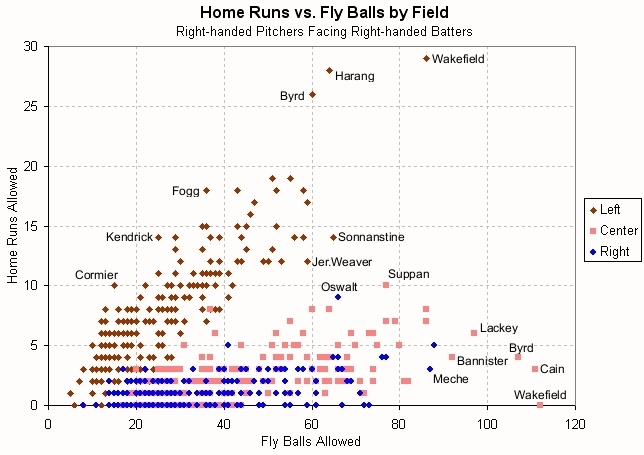
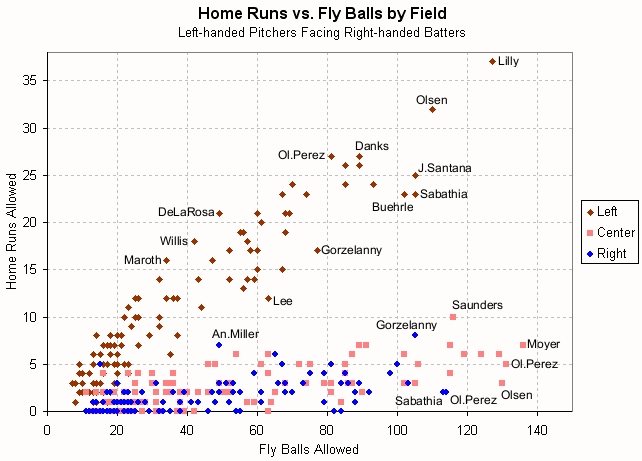
There is some variation among pitchers, but the vast majority of them allow the vast majority of their home runs on pulled fly balls. The plots for pitchers facing left-handed batters look very similar, but I don’t show them here for the sake of space. What about batters?
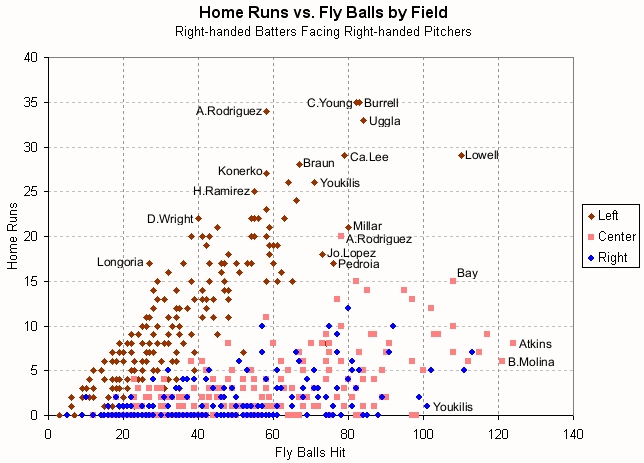
The picture for batters is similar to that of pitchers, but there appears to be more variation. Some batters are able to hit more home runs on flies hit to center or the opposite field.
Within any given season, the number of pulled fly balls a pitcher allows or a batter hits is a good indicator for how many home runs he will allow or hit, moreso than his total number of fly balls to all fields. But is this a consistent skill from year to year, for pitchers or for batters, that would allow us to improve our predictions of how players will perform in the future?
To examine this question, I split each player’s fly balls from 2007-2008 into two approximately equal halves, with odd-numbered at bats in one group and even-numbered at bats in the other group. Then I compared the percentage of fly balls that were hit to the pull field in each of the two samples.

The above graph compares the pulled fly ball percentage between the two halves for each right-handed batter with at least 50 fly balls in 2007-8. There is a pretty good correlation between the two halves, indicating that there is probably a real skill at play here. Of course, that does not come as a surprise. We know that some hitters are “pull hitters”, and I doubt it shocks you to see names like Marcus Thames and Gary Sheffield at the top of the list.
I divided the hitters into flyball hitters and groundball hitters and repeated the exercise for each group, but I didn’t see much difference in split half correlation between them. My level of statistical analysis here was admittedly at a surface level. I wanted to satisfy myself that I could detect some persistent flyball pull skill among batters, and I did that. Someone who wanted to investigate using this information to improve predictions of future batter performance would need to conduct a more thorough statistical study using larger sample sizes, for starters.
Does the same finding hold true for pitchers?
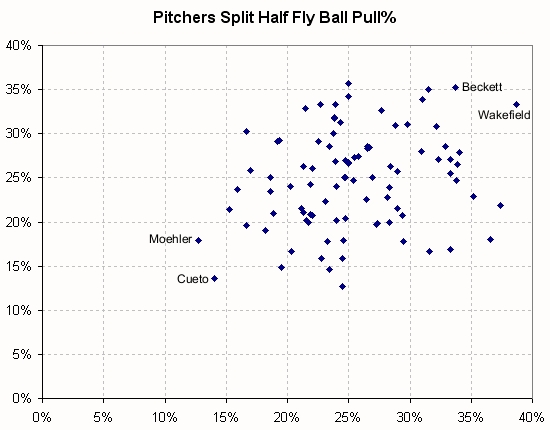
We certainly don’t see the same obvious correlation between sample halves that we did with batters. If you focus on the pitchers with the most fly balls allowed, there is some suggestion of a correlation, but if it’s there, we will probably need bigger sample sizes to reliably detect it. It may also be that some pitchers have a skill at preventing pulled fly balls or a persistent susceptibility to allowing them while at the same time it is essentially random chance for most pitchers.
One way to increase the sample size is to aggregate the pitchers into groups and perform what Mitchel Lichtman calls a poor man’s correlation. If we divide the pitchers into five groups based on their pulled fly ball percentage in the first split half sample, we get a sample size of about 3000 fly balls for each group in each half sample.
Group Sample 1 Pull% Sample 2 Pull% Highest 38.9% 27.2% 2nd 29.8% 25.6% 3rd 25.1% 26.2% 4th 21.8% 24.1% Lowest 13.7% 23.8%
We can see that the pitchers as a group maintain about 15% of their pulled fly ball percentage above or below average between halves of the sample. Again, it’s not a great correlation, but there is some indication of a real skill in which we can have a little more confidence given these much larger sample sizes.
Tim Wakefield’s data certainly implies that his pattern of fly balls allowed is anything but random. Not only does he have one of the highest allowed pull percentages in both halves of his sample, but he also allowed only one home run on the 150 fly balls that were not pulled. It seems that if you can hit a knuckleball squarely, it’s relatively easy to pull it over the fence, but if you don’t hit it squarely, you’re not going to get lucky and hit it out of the park to the opposite field. Or perhaps there is some other physics at play with the collision between bat and knuckleball; nonetheless, Wakefield stands out here.
Where do we go from here?
We have seen that the direction a fly ball is hit has a huge effect on the home run chances for that fly ball and also affects the batting average even if the ball stays in the park. A fly ball hit to the batter’s pull field is more than six times as likely to leave the park as a fly ball hit to center or the opposite field, and flyball BABIP improves by over 50 points to the pull field.
We also found that whether or not a batter pulls the ball in the air appears to be a persistent characteristic, and it appears that pitchers may have a similarly persistent but much weaker characteristic in the fly balls they allow. Adding the 2005-6 MLBAM Gameday data to the sample would help detect the pitcher skill, if it exists, for some or all pitchers.
It would also be helpful to look at the data divided by pitch type. For many individual pitchers I have noted that while their overall batted ball type and location distribution appears fairly random, when the same data is separated by pitch type and handedness of the opposing batter, there are distinct and obvious patterns. To this end, I have been developing a physical model of the ball-bat collision to see if I can quantify the difference between weak and solid contact and the associated batted ball results. That model is hopefully a subject of a future article.
References & Resources
Here are some high points from researchers who followed McCracken. I grateful to all of them for sharing their work, and I express particular appreciation to Pizza Cutter, Alan Nathan, Peter Jensen, Greg Rybarczyk, David Gassko, and Colin Wyers for their helpful conversations and assistance.
Soon after McCracken’s original work, additional rec.sport.baseball group discussion on the topic between McCracken and Eric Van focused on the question of whether pitchers display a detectable BABIP skill at the career level.
In 2001, Keith Woolner studied McCracken’s conclusions at the career level, and his conclusions are worth repeating here in full:
1. As suggested by the analysis of the standard deviation over a single season, one year’s worth of data may not be sufficient to discern a pitcher’s true level of ability with regard to ball-in-play average. It’s only when many years of data are examined that the trends become clearer.
2. Another possibility is that while the majority of pitchers have no such ability to affect ball-in-play average, a few special pitchers do have such an ability. Those whose ability allows them to systematically reduce their ball-in-play average below the overall league average would have a survival advantage, and therefore are more likely to be the pitchers whose careers are long enough to be detected in a 10-year sample. Slightly more than half (56%) of the longer-career 70 pitcher sample had ball-in-play rates below the median rate of the 338 pitcher sample that includes shorter careers. This lends some support to the notion that the long-career pitchers are somewhat better at reducing balls-in-play than their more typical counterparts. However, the evidence for this theory is not overwhelming.
3. Another line of reasoning might go as follows: When pitchers first arrive in the majors, they are still learning their craft, and in particular have not yet learned how to tailor their pitching to the defense behind them. Over time, playing with various teammates and parks over the years, a pitcher learns more about how to maximize the benefit they get from their defense. Pitchers who’ve mastered this skill get more effective defensive play behind them than less experienced pitchers on the same staff. This wisdom that comes with experience allows veteran pitchers to systematically do better with their defense, thus a skill related to preventing balls in play from becoming hits emerges.
In 2002, McCracken published DIPS 2.0, with several refinements to his original work, including adjustments for knuckleball pitchers, left-handed and right-handed pitchers, and pitchers’ strikeout rates.
In 2003, Tom Tippett took McCracken’s work, which was based on data from two or three seasons, and extended the study to cover the period 1913-2002. He found a number of pitchers who were able to suppress the opponents’ batting average over the course of a career. In addition, he found some year-to-year correlation in a pitcher’s batting average allowed on balls in play (BABIP), albeit a weaker correlation than that for strikeouts, walks, or home runs. Tippett posted some follow-up thoughts in his blog.
Tom Tango, Erik Allen, Arvin Hsu, and others worked out a method to apportion the credit for an observed pitcher BABIP rate between luck, true pitcher skill, fielding skill, and park effects in a discussion on Baseball Primer. Tango has summarized the discussion at his site.
Robert Dudek wrote an article entitled “Hang Time on the Baseball Field” for the 2004 Hardball Times Annual. He found that the hang time of a fly ball was a much stronger indicator than landing zone of whether the ball would be turned in an out. In addition, he found that that the fly balls allowed by flyball pitchers were easier to field than the fly balls allowed by groundball pitchers.
In 2004, Mitchel Lichtman used play-by-play data to examine BABIP correlations based upon batted ball types. He found, among other things, that “good pitchers probably tend to give up fewer and softer line drives and easier pop flies than do poorer pitchers.”
Nate Silver observed that a pitcher’s groundball-to-flyball ratio was one of the most consistent pitching metrics from year to year and that past groundball rate could be a valuable predictor for future home run rate.
In 2005, research by John Burnson found that pitchers don’t have much impact on their rate of home runs allowed other than the extent to which they allow outfield flies in general. Dave Studeman took this concept and created the xFIP statistic, normalizing not only a pitcher’s BABIP rate but also his rate of home runs allowed per outfield fly ball.
J.C. Bradbury investigated whether the DIPS components had a predictive affect on future BABIP and found that a pitcher’s strikeout rate indeed was a factor in explaining future BABIP rates, confirming McCracken’s work on DIPS 2.0. He added some additional comments later at his blog.
Clay Davenport examined the BABIP allowed by minor league pitchers and found that those pitchers who were eventually promoted to the major leagues allowed a lower BABIP than those who did not make the majors. One possible explanation is that, while differences in BABIP skill among major league pitchers may be small, they may nonetheless demonstrate BABIP skill that is not common among all pitchers at lower levels because major league pitchers are selected partially for this skill.
David Gassko presented a DIPS 3.0 formula that took into account the frequency of batted ball types allowed by the pitchers. In the 2006 Hardball Times Annual, Gassko and Bradbury examined to what extent batters and pitchers control their batted balls based upon batted ball type data from Baseball Info Solutions. In the 2007 Hardball Times Annual, Gassko expanded and refined this examination. Among his other findings is a key one about home runs.
Last year, JC and I concluded that pitchers do not have much, if any, impact on the percentage of outfield flies that go over the fence. Further examination of the data shows this to be wrong. Pitchers clearly have some, though not much impact on the number of home runs they allow per outfield fly. Some of this correlation is due to park, but even adjusting for park effects, the correlation is still significant. These numbers also match the results Lichtman reported to me in a private e-mail. What this means is that we should pay attention to the numbers of home runs a pitcher allows per fly ball, but with one year of data, we should also be wary of pitchers with highly unusual numbers of home runs per outfield fly.
In 2006, Gassko updated his DIPS 3.0 formula, substituting league average line drive percentage for a pitcher’s actual allowed line drive percentage, although he later called this new statistic LIPS. Gassko also observed that groundball pitchers’ mistakes tend to end up as line drives, moreso than they do for flyball pitchers.
What this finding also means is that ground ball pitchers do not have as much of an advantage over fly ball pitchers as some might think. Being a ground ball pitcher may help suppress home run rates; it does nothing for line drive rates.
Findings by Gassko and Dave Studeman indicated that DIPS might not apply as well to closers as it does to starting pitchers.
In 2007, Tom Tango presented results of a study on pitcher career BABIP performance showing that the distribution of BABIP was very unsymmetrical, being skewed toward outperforming the average BABIP expectation relative to teammates. Tango also developed a shorthand regression equation for pitcher BABIP.
In 2008 and 2009 at Statistically Speaking, Pizza Cutter studied the amount of balls in play needed to reliably measure pitcher BABIP skill and home run rate per outfield fly ball, as well as other pitching statistics.
A few other DIPS-related pitching metrics are worth mentioning. Clay Dreslough created Defense-Independent Component ERA (DICE) in 2001, although its close cousin, Fielding Independent Pitching (FIP), created by Tom Tango, is more widely used. Both metrics use the DIPS components to produce an ERA estimator independent of fielding influences but simpler to calculate than McCracken’s full DIPS ERA formula. A newer statistic developed by Graham MacAree is tRA, which uses the average run values and out values for each batted ball type in order to estimate the runs allowed average that should be credited to the pitcher.
