Dynamic Run Value of Throwing a Strike (Instead of a Ball)

Jordan Zimmermann was one of the best at getting a first-pitch strike in 2014. (via Alan Kotok)
The importance of the first pitch in an at-bat has been well documented. A favorable count for a hitter can make a bench bat into a feared slugger, while a favorable count for a pitcher can make a mop-up man into an ace. As the count gets deeper and the at-bat approaches its conclusion the expected result can swing drastically in favor of one party or another. How exactly do the odds swing with each pitch?
We can tabulate average wOBA values at each step in the count and then convert them into a run value for a strike or a ball in any count. Prior work has examined the run value of a strike, but in limited contexts. I will calculate the value of a strike by count and in a neutral context. We normally think of these values as static. I will show how these values have changed as the run scoring environment has become depressed and how these values are affected by the quality of hitter. Finally I will explore why these values change the way they do.
These run values can be used in a variety of ways. I will focus on the use of a run value measure to be used at the heart of a catcher framing metric. The calculations can also be useful in other contexts, for example, awareness of the value of a strike in different counts can help dictate strategy.
Review of Prior Work
Assigning run values to a strike at each step in the count is not a novel concept. In fact, such work predates PITCHf/x data itself. Craig Burley examined the issue here at The Hardball Times back in 2004. Using data from Tom Tippet’s Diamond Mind Baseball, Burley calculated league batting average, on-base percentage, and slugging percentage at each count after a ball and after a strike. Then, using linear weights Burley calculated the run value associated with a ball or strike in each count. Here are Burley’s results:
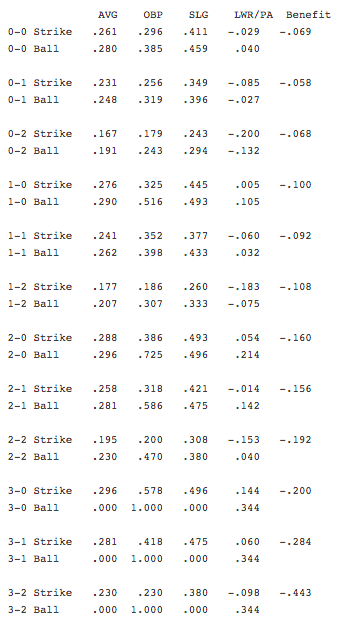
Burley’s table is set up in a long format such that we may read the expected performance and value of a ball or a strike in each count. We can read that in an 0-0 count a strike leads to decreased expected batter performance and a linear weight value of -.029. If that at-bat starts with a ball, the expected hitter performance increases to the tune of .040 linear weight runs per plate appearance. Thus, the net benefit of a first pitch strike is -.069 runs.
More recently, Dan Brooks and Harry Pavlidis presented a run value matrix in their fantastic piece at Baseball Prospectus where they introduced their regressed probabilistic model for measuring catcher defense. Brooks and Pavlidis use data from 2008-2013 and arrive at slightly larger run estimates for the run value of a strike in each count:
| Run Value Matrix (Brooks/Pavlidis, BP, 2014) |
|---|
| Ball | Strike | Maximum Framing Run Value Available |
| 0 | 0 | 0.080 |
| 0 | 1 | 0.092 |
| 0 | 2 | 0.199 |
| 1 | 0 | 0.112 |
| 1 | 1 | 0.117 |
| 1 | 2 | 0.241 |
| 2 | 0 | 0.156 |
| 2 | 1 | 0.098 |
| 2 | 2 | 0.339 |
| 3 | 0 | 0.173 |
| 3 | 1 | 0.251 |
| 3 | 2 | 0.590 |
Brooks and Pavlidis report a weighted context-neutral average of about 0.14 runs per ball to strike.
Methods
After loading PITCHf/x data for 2014 (downloaded from Jeff Zimmerman’s BaseballHeatmaps.com), I grouped the data by count, calculating the wOBA for each at-bat that contained that count. Every at-bat starts with an 0-0 count, thus this wOBA corresponds to the league average wOBA — in 2014 that was .310. With the wOBA calculated at each count the next step is to calculate the transitions from each count to the two possible options that continue the at-bat, a ball is thrown or a strike is thrown. These transitions from expected performance count to count will be the basis for our run value per strike.
If a strike is thrown in a two-strike count, the resulting wOBA is .000. Thus, a strike in a two-strike count transitions the batter from their starting wOBA in the two-strike count to a wOBA of .000. Similarly, if a ball is thrown in a three-ball count this transitions the batter to a walk, in 2014 that means a wOBA of .689.
Before getting to the results, a quick note on two-strike fouls. I filtered all two-strike fouls, as these pitches do not advance the count or end the at-bat. Because of the way I grouped by count, if I had left them included, this would mean including an extra instance of the at-bats result for each two-strike foul. For instance, an at-bat with an 0-2 count and three two-strike fouls that ended in a strikeout would collapse to be one at-bat that resulted three strikeouts. That would be very bad.
Results
By Count Run Value Matrix
We run the above analysis on 2014 PITCHf/x data and arrive at the matrix you see below. The first column is the count before the pitch is thrown.
Under the wOBA heading, “Start” refers to the average wOBA players achieve on at-bats that contained that count. “Strike” and “Ball” refer to the average wOBA players achieve on at-bats containing that listed count with an additional strike or ball. If this resulted in a strikeout or a walk the “Strike” and “Ball” will be .000 and .689 respectively.
Under the Delta heading, “Strike” and “Ball” refer to the difference in wOBA between the starting wOBA and the strike or ball wOBA. The sign on these values matters, as a strike results in a negative delta and a ball in a positive delta. The “Total” is the difference in wOBA between the strike and ball wOBA and the “Run Value” column converts that wOBA difference to a per plate appearance run value by dividing the wOBA delta by that years wOBA scale.
For the columns “Total” and “Run Value,” we have just taken the positive value, the total delta or run value of a ball in that count. To get the value of a strike, simply take the negative of that value.
| Run Value Matrix (2014) |
|---|
| wOBA | Delta | ||||||
|---|---|---|---|---|---|---|---|
| Count | Start | Strike | Ball | Strike | Ball | Total | Run Value |
| 0-0 | .310 | .262 | .355 | -.048 | .045 | .093 | 0.071 |
| 0-1 | .262 | .196 | .293 | -.066 | .031 | .097 | 0.074 |
| 0-2 | .196 | .000 | .223 | -.196 | .027 | .223 | 0.171 |
| 1-0 | .355 | .293 | .436 | -.062 | .081 | .143 | 0.110 |
| 1-1 | .293 | .223 | .352 | -.070 | .059 | .129 | 0.099 |
| 1-2 | .223 | .000 | .273 | -.223 | .050 | .273 | 0.210 |
| 2-0 | .436 | .352 | .622 | -.084 | .186 | .270 | 0.207 |
| 2-1 | .352 | .273 | .470 | -.079 | .118 | .197 | 0.151 |
| 2-2 | .273 | .000 | .384 | -.273 | .111 | .384 | 0.295 |
| 3-0 | .622 | .470 | .689 | -.152 | .067 | .219 | 0.168 |
| 3-1 | .470 | .384 | .689 | -.086 | .219 | .305 | 0.234 |
| 3-2 | .384 | .000 | .689 | -.384 | .305 | .689 | 0.528 |
The numbers should not come as too much of a shock. A league average hitter with one strike on him sees his production fall by nearly 50 points of wOBA. The swing is nearly 100 points of wOBA or 0.071 runs between a first-pitch strike and a first-pitch ball. Deeper into the count, the stakes are much higher, as we would expect.
The largest total delta on a non at-bat ending pitch is in a 2-0 count. At the start of a 2-0 count, the batter has an average wOBA of .426. A strike to put things at 2-1 brings him down to an earthly .352 wOBA, but a ball bringing him to 3-0 makes him to an immortal .622. The total swing on a 2-0 pitch is .270 wOBA points or 0.207 runs. The pitcher should do everything short of laying one in to avoid a 3-0 count.
The largest total delta period, of course, comes with a full count where a pitch that is not put in play (or fouled) will surely end the at-bat with a walk for a .689 wOBA or a strikeout for a .000 wOBA. The total run value on a ball versus a strike in a full count is a whopping 0.528.
A Singular Value
Arriving at a singular, context-neutral run value is as simple as taking the mean weighted by the number of pitches in that count. However, depending on our use we will want to weight by different sums of pitches.
If we want a metric to use for catcher framing metrics we should weight by pitches seen and not swung at. That is, we want to weight by framing opportunities where a framing opportunity is a pitch that is not swung at. We will, for our purposes, assume there are no further biases in terms of what pitches are actually frameable than that they are simply not swung at.
If we want a general metric, we don’t care if the pitch is swung at. We will want to weight by pitches that resulted in a ball, strike, strikeout, or walk. That is, we want all balls that were not put in play.
Below is a table with the number of pitches thrown in each count, the number of pitches seen in each count, and the number of pitches not put in play in each count.
Additionally, we have columns for the percent of pitches that were thrown in that count. For example, in 2014, 26.6 percent of all pitches thrown were in an 0-0 count, 35.8 percent of all pitches taken were in an 0-0 count, and 28.9 percent of all pitches not put in play were in an 0-0 count.
| Pitch Totals by Count (2014) |
|---|
| Total Pitches | Pitches Seen | Pitches Not In Play | ||||
|---|---|---|---|---|---|---|
| Count | # | % | # | % | # | % |
| 0-0 | 165,653 | 26.6% | 117,585 | 35.8% | 146,007 | 28.9% |
| 0-1 | 80,870 | 13.0% | 42,019 | 12.8% | 65,967 | 13.0% |
| 0-2 | 40,278 | 6.5% | 19,613 | 6.0% | 33,028 | 6.5% |
| 1-0 | 63,390 | 10.2% | 36,114 | 11.0% | 52,463 | 10.4% |
| 1-1 | 63,503 | 10.2% | 28,673 | 8.7% | 49,639 | 9.8% |
| 1-2 | 58,478 | 9.4% | 24,452 | 7.5% | 45,821 | 9.1% |
| 2-0 | 21,391 | 3.4% | 11,816 | 3.6% | 17,562 | 3.5% |
| 2-1 | 31,836 | 5.1% | 12,783 | 3.9% | 23,788 | 4.7% |
| 2-2 | 48,998 | 7.9% | 16,534 | 5.0% | 36,107 | 7.1% |
| 3-0 | 7,010 | 1.1% | 5,611 | 1.7% | 6,736 | 1.3% |
| 3-1 | 12,930 | 2.1% | 5,608 | 1.7% | 9,645 | 1.9% |
| 3-2 | 28,477 | 4.6% | 7,386 | 2.3% | 19,230 | 3.8% |
| Total | 622,814 | 100.0% | 328,194 | 100.0% | 505,993 | 100.0% |
To find our run value to use for catcher framing, we weight by pitches seen and arrive at an average run value of 0.128 runs per ball to strike. If we use our same weights, the run values reported by Brooks and Pavlidis we arrive at 0.140! Exactly the value they reported. We seem to agree in terms of how to weight the run value results for the purposes of catcher framing. The disagreement in values, 0.128 versus 0.140, could be due to the fact that my 0.128 value is specific to the 2014 season while they reported an average across 2008-2013.
To arrive at a general metric, we weight by all pitches not put in play, not just pitches seen. When we do this, we arrive at an average run value of… 0.143. It makes sense that this value is higher. Hitters are less likely to look at a pitch deep in the count so we get a heavier weighting toward the higher leverage counts.
Year-to-Year Run Values and the Depressed Run Scoring Environment
The current run-scoring environment is marked by depressed offense. We should expect decreased run scoring to affect our average run values. We can examine the run values calculated year-by-year going back to 2010.
| Yearly Run Values of a Strike |
|---|
| Year | wOBA | Run Value (By Pitches Seen) | Run Value (By Pitches Not In Play) |
| 2010 | .3240 | 0.141 | 0.157 |
| 2011 | .3181 | 0.137 | 0.152 |
| 2012 | .3168 | 0.137 | 0.153 |
| 2013 | .3146 | 0.133 | 0.148 |
| 2014 | .3098 | 0.128 | 0.143 |
| Mean | .3167 | 0.135 | 0.151 |
We see there appears to be a strong correlation between wOBA and the calculated average run value for a ball to strike. In fact the two have a correlation coefficient of 0.98! We can see the closeness of fit in this plot of wOBA values versus Run Values for 2010-2014. We will use the values weighted by pitches seen, as we would use for a catcher framing metric, from here on out.
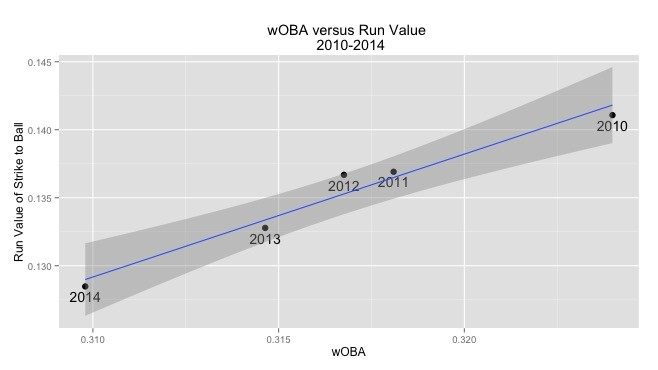
This fit is suspiciously high, but because the run values are all based on the wOBA differences from count to count there is no mechanical reason why the run values need to be so closely associated with wOBA.
There are two possible reasons for this association. The by count wOBA expectations could be changing, meaning the decreased offense disproportionately affects hitters at different points in the count. Another possible reason for this association is the distribution of counts and weights are changing, hitters are finding themselves in high leverage deeper counts less often. Let’s examine these possibilities.
1) By Count wOBA Expectations are Changing
If this is the case, it is because hitters are not performing more poorly in pitcher’s counts as they are performing more poorly overall. This is certainly plausible and we can check this by examining the yearly changes in wOBA by count independent of our weighting. The following color-coded tables show the change in ball to strike run values:


Since 2010, wOBA has declined 14 points (the 0-0 row corresponds to league average wOBA). However, the decline is not proportional across counts. The depressed run environment disproportionately affects hitters in deeper counts. In 2014, league average wOBA was down 14 points, but in 0-2 counts it was only down five points. In 3-0 counts, however, wOBA was down a whopping 39 points. Hitters had a worse time in 3-0 counts than they used to. Furthermore, they are having a worse time in 3-0 counts relative to league average than they used to.
If we observe less of a boost in hitter performance relative to league average when they get ahead in the count, this could explain why the run value of a ball to strike is dropping in magnitude.
2) By Count Proportion of Pitches Seen is Changing
An alternative explanation is that hitters are seeing a smaller percentage of pitches in higher leverage counts. If hitters are less often getting in deeper counts or are siwnging more freely in deeper counts than the higher leverage pitches get smaller weight, as there are fewer high leverage framing opportunities. Again, we can turn to a table of these values over time and a table of the changes.


The changes are small, but the weights have shifted over time. As run scoring has fallen from 2010 to 2014, the percentage of pitches taken early in the count is on the rise, while pitches taken in deeper and hitter friendly counts has dropped. Pitches taken in a 1-0, 2-0, and 3-0, count have dropped in share by 0.7, 0.5, and 0.3 percentage points respectively. Meanwhile, pitches taken in 0-1, 0-2, and 1-2 counts have risen in share by 0.5, 0.4, and 0.5 percentage points respectively. This would result in a heavier weighting toward lower valued pitches and would also contribute to the lower average value of converting a ball to a strike in today’s game.
Overall, we are seeing that as the run-scoring environment evolves the deep count pitches are both relatively less high leverage than they used to be, and there are fewer framing opportunities per pitch in that count, as hitters are taking fewer pitches in hitter friendly counts.
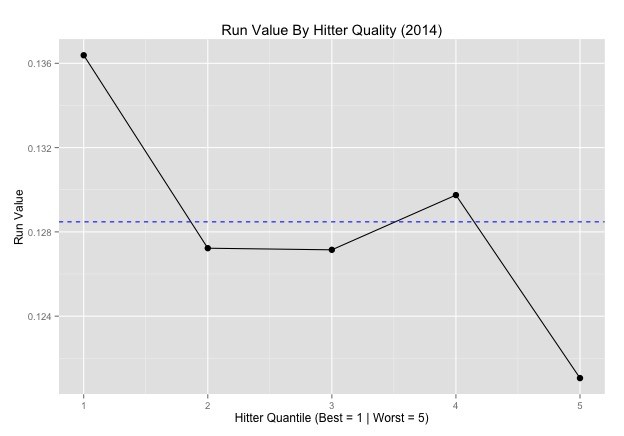
By Quality of Hitter Run Values
If we have established a tie between wOBA and the run value of a ball to strike, it would make sense to assume these values will also vary by quality of hitter. We can run our run value calculations for different quantiles of hitter based on their yearly wOBA (250 PA limit). Unsurprisingly, a strike against a better hitter is worth more.
| Run Value By Hitter Quality (2014) |
|---|
| Hitter Quality | wOBA | Run Value (By Pitches Seen) | Run Value (By Pitches Not in Play) |
| Best | 0.382 | 0.136 | 0.153 |
| Good | 0.337 | 0.127 | 0.143 |
| Middle | 0.320 | 0.127 | 0.143 |
| Bad | 0.302 | 0.130 | 0.145 |
| Worst | 0.275 | 0.121 | 0.135 |
| All | 0.310 | 0.128 | 0.143 |
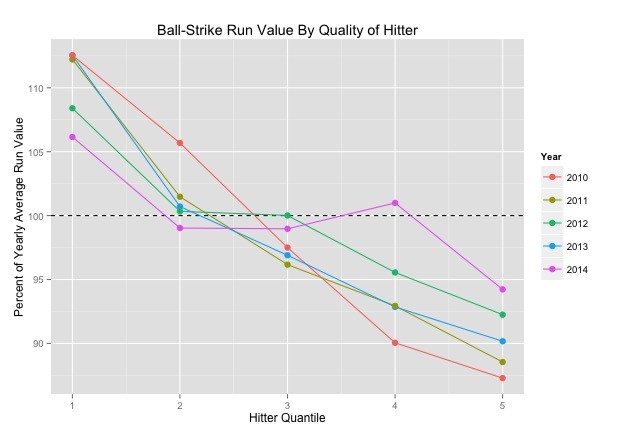
Here is the trend for the last five seasons, normalized to each year’s baseline run value to account for the fact the run values have been going down.
It makes sense that a strike is most valuable against better hitters; here is how each class of hitter fared in at-bats containing each count.
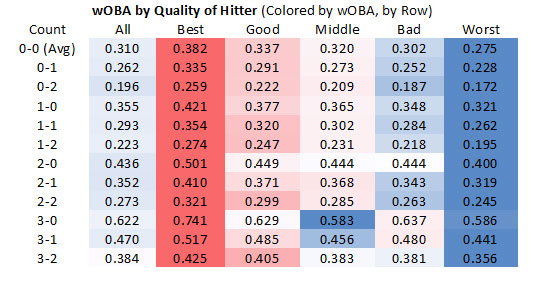
This table shows the differences of each class from the best hitters. It is colored by column to facilitate comparison of how different classes of hitter differ by count.
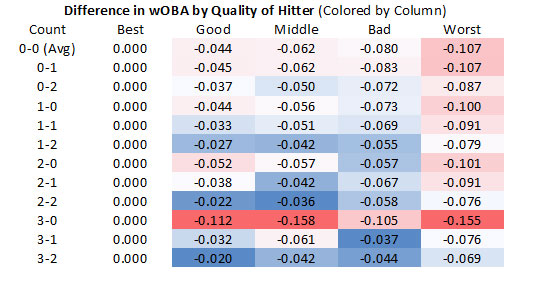
The best hitters appear to be the best in part because of their ability to take advantage of the 3-0 count. In total the best hitters have a wOBA that is .044 better than good hitters. The advantage however jumps to .112 in at-bats containing 3-0 counts. The takeaway here is that the best hitters are not better in fixed proportions across counts, but they really excel in hitter’s counts.
As with our yearly analysis, we can also examine good hitters’ ability to get in these counts more often. Here is a table of what percentage of pitches taken fall in what count by hitter quality.
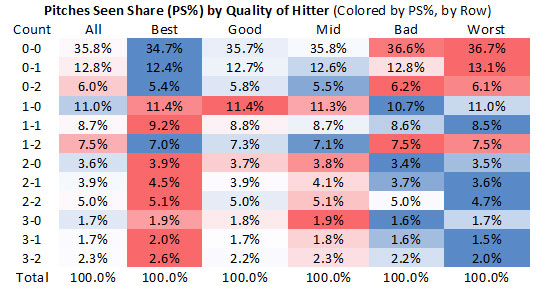

We find the best hitters are not only doing better in deep counts, but they find themselves taking more pitches in these counts, which allows for more framing opportunities by the catcher. This means that framing opportunities against better hitters more often come later in the count, so if we are examining better hitters it makes sense to use a higher run value measure.
References & Resources
- Craig Burley, The Hardball Times, “The Importance Of Strike One (and Two, and Three…), Part 2”
- Harry Pavlidis and Dan Brooks, Baseball Prospectus, “Framing and Blocking Pitches: A Regressed, Probabilistic Model”
One other impact of framing/umpiring skill: the more extreme the skill/bias, the more likely hitters will change their behavior for the entire game, resulting in effects that go well beyond a single pitch becoming a called ball or strike.
On the larger decline in wOBA in hitters’ counts: this is just a function of the number of opportunities at each count for a worse outcome for the hitter. In these counts, there are just many more positive outcomes (for hitter) that can become outs in a lower-offense environment. At 0-2 the hitter was already making outs at a huge rate, and those outcomes can’t get any worse. But at 3-1, many positive outcomes can become outs as offense declines. If you compare wOBA and decline in wOBA by count, you will see there is nearly a perfect correlation.
On the .98 correlation of wOBA and strike value: doesn’t this have to be true, mathematically? The (negative) run value of a strikeout rises proportionately as scoring increases. Meanwhile, the value of a BB will rise as offensive increases (more likely to score when on base). So the spread between strikes and balls must increase as offensive levels rise.