Fly Ball Carry and the Home Run Surge

Nelson Cruz is among the leaders in fly ball distance, and could benefit from extra carry. (via Keith Allison)
Editor’s Note: This piece initially was given as a presentation at the marvelous 2017 Saberseminar.
One topic that seems to be consuming the baseball world these days is the surge in home runs in the major leagues, starting approximately midseason in 2015. I won’t attempt to document all the data or all the articles that have searched for reasons for the surge. I do want to refer to two recent articles that address one possible reason for it.
Writing for The Ringer, Ben Lindbergh discussed measurements on the size, weight and seam height of baseballs, and suggested changes in these properties might result in increased distances of fly balls, leading to more home runs.
Writing for FiveThirtyEight, Rob Arthur tooks this basic idea much further. Using the voluminous amount of pitch-tracking data from both PITCHf/x and Statcast–and specifically by looking at the speed lost when traversing the distance from release to home plate–he suggested the air drag on the baseball has gotten smaller in the past several years, and the reduction in air drag is correlated with the increase in home runs per fly ball.
Both of the recent articles suggest part of the home run surge can be explained by better “carry” (a term I will define more carefully later on) on a fly ball, presumably due to properties of the ball that have changed in such a way as to reduce the air drag. That is the issue I want to focus on here, using a very different analysis technique.
This topic was the primary subject of my talk at the 2017 Saberseminar a couple of weeks ago. Consider this article a written version of that talk with a few more details thrown in. For people who like to see a lot of equations and other technical stuff, I have written up a more detailed version.
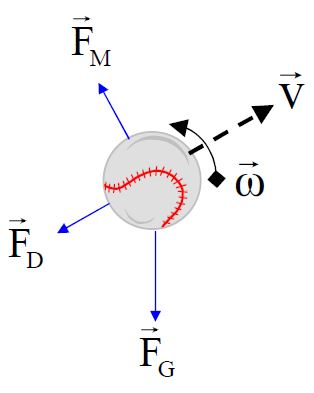
Let’s starts with some background. When a spinning baseball travels through the air, it experiences three forces, as shown in Figure 1. Gravity pulls the ball downward; drag slows it down; and “lift,” or the Magnus force (assuming the ball is spinning), changes its direction. If baseball were played in a vacuum (the “Physics 101 world”), it would only experience gravity. Under such conditions, the initial position and velocity (i.e., speed, launch angle, and direction) of a fly ball would uniquely determine where it lands and how long it took to get there.
However, our world is more complicated than the Physics 101 world. As a simple example, consider a typical home run hit with an exit velocity of 100 mph at the optimum launch angle of 27.50, which travels just about 400 ft. In the Physics 101 world, that ball would travel 555 ft. And if the ball were hit with the same exit velocity but at the optimum Physics 101 launch angle of 450, it would travel 673 ft.
So the drag and lift on the baseball really do matter…a lot! Generally speaking, drag reduces the carry and lift (assuming it is the result of backspin) increases the carry. But the effect of drag on carry is far greater than the effect of lift. Therefore, in the discussion to come, I will focus on drag.
One of the consequences of not living in a Physics 101 world is that the ball sometimes carries differently than it did at other times. We even hear the broadcasters say things like, “The ball is really carrying well tonight.” What do they mean by that? Well, what they mean (whether they realize it or—more likely—not) is that the drag on the baseball is different from what it usually is.
One of the more dramatic examples of that occurs essentially every day at Coors Field in Denver, where the thin air (i.e., reduced air density) results in reduced drag and therefore better “carry.” Better carry also can occur if the temperature is particularly high, resulting in lower air density (hence, reduced drag); and of course, the opposite occurs if the temperature is particularly low. And the wind, especially headwind or tailwind, can have an enormous effect on the carry. Most people who follow baseball closely have developed an intuitive feel for how changes in atmospheric conditions affect the carry of a fly ball.
However, the drag on the baseball depends on more than just atmospheric conditions. It also depends on specific properties of the baseball: the size, the mass, and the so-called drag coefficient (CD). One way to think about these properties is as follows. As the ball moves through the air, it has to push the air molecules out of the way. So the ball exerts a force on the air. As a consequence, Newton’s Third Law (often called the “action-reaction” law) says the air exerts an equal force on the ball in the opposite direction, slowing down the ball. With that picture in mind, you can see why lower air density means lower drag: The ball has to push fewer air molecules out of the way.
But as I said, properties of the ball matter also. The larger the ball, the more air it has to push out of the way, resulting in a larger drag force and less carry. The drag force causes the ball to slow down (i.e., to decelerate), where the rate of deceleration is inversely proportional to the mass (Newton’s Second Law, F=ma, or better a=F/m). Therefore, a heavier ball has less deceleration, resulting in greater carry.
The tricky one to discuss is the drag coefficient CD, which is sort of a fudge factor reflecting the fact that ball doesn’t have to push the air completely out of the way, since the air can sort of slide around the ball. The drag force is directly proportional to CD, so that a larger value of CD means greater drag and less carry. Generally, CD depends on the surface properties of the ball and quite possibly on the height of the seams. I’ll return to this point later on.
So the carry of a fly ball depends on both atmospheric conditions (temperature, elevation, wind, etc.) and properties of the ball. In both of the recent articles I mentioned earlier, it has been proposed that the carry has increased in the past two years in part due to a change in the properties of the ball that affect the drag. Clearly, if one wants see whether a change in carry could be attributed to the baseball, it is important to control for atmospheric effects.
With that in mind, let me now get to the point of this article. What I have done is analyzed the trajectories of fly balls at Tropicana Field for games starting with the 2015 season and extending to the All-Star break of the 2017 season. Since the Trop is a covered stadium 100 percent of the time, the atmospheric effects can reasonably be expected to be constant, with no wind. Since we are primarily interested in long fly balls, the ones that might result in home runs, I restricted the analysis to balls hit with an exit velocity greater than 90 mph and launch angles in the range 200-350, typically leading to distances greater than 300 feet. The data were grouped into five different sets labeled as follows:
- y15E: Pre-All-Star Game, 2015
- y15L: Post-All-Star Game, 2015
- y16b: Half of 2016 data, randomly selected as a training set, as discussed below
- y16a: Remainder of 2016 data
- y17E: Pre-All-Star Game, 2017
One conceptually simple way to do such an analysis is to compare flyball distances under identical initial conditions, including exit velocity, launch angle, direction, spin rate and spin axis (i.e., backspin, sidespin, etc.), all of which are determined by the Statcast system. Unfortunately, that simple process cannot work, since there are not sufficient data with identical initial conditions to provide a statistically meaningful result. So instead one must resort to modeling, which I now describe. Much more of the technical details can be found in the accompanying article.
The essential idea is the following: If the initial conditions are known, and if we have a model telling us how the drag and lift depend on speed and spin, we can calculate the trajectory exactly. This is exactly how my Trajectory Calculator works: The user supplies the initial conditions, and the built-in model for drag and lift then are used to calculate the full trajectory. Actually, the original motivation for this study was to develop an improved model for drag and lift in order to produce an improved Trajectory Calculator. The analysis I present here is a serendipitous byproduct.
To develop the model, half of the 2016 data were randomly selected. I call this the “training set” and label it y16b. A total of 160 batted balls satisfied the long-flyball criteria. (A technical point: It is well known that Trackman, the part of Statcast used to track the baseball, does not track every fly ball to its landing point. For the current study, only fly balls tracked to at least 90 percent of the full distance were utilized, thereby assuring the most accurate measurements of the distances.) The model involved five initially unknown parameters, which were adjusted to best fit each trajectory.
There is considerable ball-to-ball variation in these five parameters, suggesting the drag and lift properties of the baseballs are not uniform. This is not particularly a new result and has previously been observed in both pitched and batted-ball analysis. What matters for present purposes is whether the average drag and lift properties have changed. Therefore, in our model we use values of the five parameters that are averaged over all 160 trajectories.
So, armed with a model for drag and lift that describes, on average, the y16b trajectories, for each of the other four data sets I can use that same model along with the initial conditions to calculate the trajectories, determine the flyball distance, and compare with the actual distance. The results are shown in the table and two figures below (Figures 2-3).
| Data Set | # of Trajectories | Δ±err (ft) |
|---|---|---|
| y15E | 133 | -4.8±0.8 |
| y15L | 100 | -1.6±1.2 |
| y16a | 169 | 0.5±0.7 |
| y16b | 160 | 0.0±0.8 |
| y17E | 199 | 0.1±0.7 |
| 2016-2017 | 528 | 0.2±0.4 |
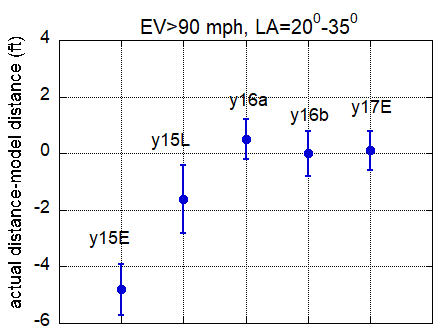
Figure 2: Mean difference between actual and calculated distances, using the model obtained from y16b. The bars are the standard error on the mean.
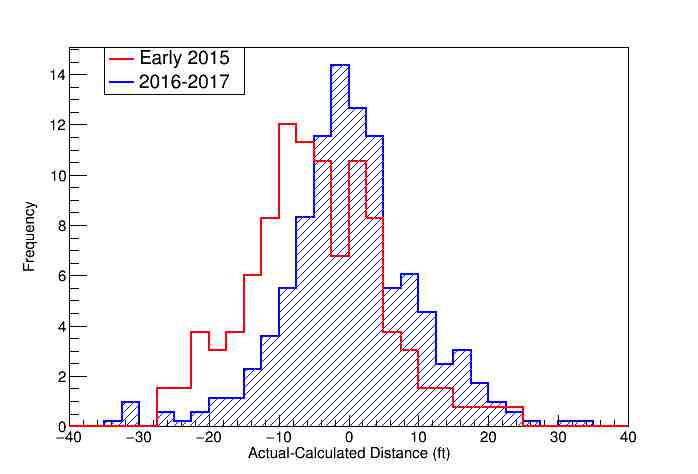
Figure 3: Histogram of differences between actual and calculated distances for the y15E data (red) and all 2016-17 data (shaded).
First refer to Figure 2, which shows the mean differences between the actual and calculated distances (hereafter referred to as Δ) based on the model for drag and lift developed with the y16b data set. The same results are shown in tabular form in the table. Here are some comments on these results:
- Δ=0 for the y16b data set, which should be no surprise since the model was constrained to fit those trajectories.
- Δ~~0 for the y16a data set. Since the separation of the 2016 data into the two sets was done randomly, it is a good test of the self-consistency of the analysis procedure that we also obtain 0 for y16a.
- Δ=-4.8 ft for y15E, meaning the actual drag on the baseball in that data set is greater than that for 2016, on average, resulting in an actual distance less than the calculated distanced based on the 2016 drag.
- An intermediate result is obtained for y15L.
- There is no apparent difference in distance, and therefore in drag, between 2017 and 2016.
Since the results for both 2016 sets and the 2017 set look essentially identical, I have combined them in the last line of the table to produce Δ=0.2.
Thus we find that the ball carries better in 2016 and 2017 relative to 2015 pre-Al-Star Game by 5.0±0.9, a statistically significant, five-standard-deviation effect. Moreover, we find the ball carries no differently in 2017 than in 2016. Finally, we find the post-All-Star Game result for 2015 is intermediate between the pre-All-Star Game and the 2016 results, suggesting the transition between “high-drag” and “low-drag” baseballs occurred gradually following the All-Star Game.
To further emphasize these results, I show in Figure 3 histograms of differences between actual and calculated distances for y15E and for all the 2016-17 data, where the two histograms have been scaled to the same number of total events. The five-foot increase in the latter relative to the former is readily apparent.
Conclusions
So what are the implications of these results for home runs production? Without presenting any details, I estimate that a five-foot increase in distance would increase home run production by about 15 percent. So the conclusion of this analysis are as follows:
- The aerodynamic properties of the baseball can account for a considerable fraction of the increase in home production from pre-All-Star Game 2015 to 2016.
- The aerodynamic properties of the baseball contribute very little to the increase from 2016 to 2017.
As is often the case, while some questions are answered, many more arise. Are the results found here compatible with those found by Rob Arthur? Is there further evidence (e.g., from pitch-tracking data) that shows a change in the drag coefficient, as Rob has suggested? If so, how is that change related to the change seen in the trajectory analysis presented here? Is a change in drag correlated with changes in the baseball that can be directly measured, such as size, mass and seam height? These and other related questions are all very interesting, and it is hoped that answers to them will be pursued in the coming months.
References & Resources
- Ben Lindbergh, The Ringer, “The Juiced Ball Is Back”
- Rob Arthur, FiveThirtyEight, “In MLB’s New Home Run Era, It’s The Baseballs That Are Juicing”
- Alan M. Nathan, Univ. of Illinois, “Analysis of Baseball Trajectories”
- Jeffrey R. Kensrud, Lloyd V. Smith, Alan M. Nathan & Derek Nevins, 7th Asia-Pacific Congress on Sports Technology/ScienceDirect, “Relating baseball seam height to carry distance”
- Alan M. Nathan, Univ. of Illinois, “What New Technologies Are Teaching Us Aboutthe Game of Baseball”
- Alan M. Nathan, 2017 Saberseminar Powerpoint Slides Download
- Alan M. Nathan, Trajectory Calculator Excel Download

Help me out here, please. I seem to recall an article at this very website some years ago concerning how many “cheap” home runs were being hit just over the outfield wall, which posited a certain percentage of long balls the chicks love would simply be outs if the fences were moved back…I’m thinking that number was also five feet.
In basketball the hoop is the same height as it was in the 1940’s and ’50s even though the players are now, on average, much taller. This has led to many calls such as this when a player dunks the ball, “What a SHOT!” I think of this when seeing yet another long fly turned into “What a HOME RUN!”
Move the fences back in every ballpark ten feet and bring back the running game, triples, and some excitement. MLB has devolved into Home Run Derby mode. Every team waits for the Earl Weaver special, the three-run homer. The DH has had much to do with the current mindset. Do away with the DH, and get back to Baseball as it was meant to be played.
You forgot the part of all those darn kids getting off of your lawn! ****shakes fist****
The Era of Encroaching Dinger Reliance
Jeff Sullivan
4
Home runs are up league-wide. Yes, yes, everyone knows that. But they’re seizing control of all run production.
http://www.fangraphs.com/
Two questions:
1) Would something changing aerodynamically indicate a change to the surface of the ball more than something internal? If so, this gibes pretty well with pitcher’s complaints about the current ball causing more blisters?
2) Does this mean reverting to the old ball would affect players like Giancarlo Stanton and Aaron Judge, who hit the ball very hard, and often at low angles, less than players with less power who are lofting it out of the park (the less time the ball is in the air, the less drag it experiences, right?) I’m a physics dummy so I might be thinking about this wrong and am wondering if someone smarter can clarify the implications.
1) The effect of drag depends on weight, size, and drag coeff. The latter is a surface property of the ball (roughness, seam height, …)
2) Good question, but it is one that I’d have to think about a bit. You can try to investigate for yourself using my Trajectory Calculator, http://baseball.physics.illinois.edu/TrajectoryCalculator-new-3D.xlsx. You can make small changes to the number in cell G2
Alan, according to MLB’s own measurements the ball has decreased in size around .01 inch since 2014 and the mass (weight) has actually gone DOWN since 2014. I have posted on twitter, once again, MLB’s 2014-2017 measurements. (Presumably 2015 is a blend of “new” and “old” balls, where “old” is similar to 2014 and “new” is similar to 2016.)
As well, if I plus mass and size numbers into your trajectory calculator, small changes have very little effect on carry. Essentially it would take a huge decrease in size (.14 inches) or increase in weight (.16 oz) to increase carry by almost 5 feet.
So it appears, using MLB’s own measurements, that size and mass changes from 2014 (and early 2015) to 2016 (and 2017) would have little or no effect on carry.
So that leaves seams. Again, according to MLB’s own data, seams have decreased in height by around .003 inches from 2014 to 2016 and 2017.
You were previously agnostic on whether small changes in seam height for the “low-seam” MLB ball had any significant effect on drag and therefore carry. Is that right? Have you changed your mind?
To be clear to the reader:
Alan found an increased carry of around 5 feet from pre-ASB 2015 to 2016 and 2017. Controlling for atmospheric conditions and launch parameters, that can only be caused by a significant reduction in ball size, increase in ball mass/weight (I think it’s worth noting that increased mass causes decreased EV such that overall, the effect on distance is pretty neutral), or a change in surface characteristics such as decreased seam height, that reduces drag.
According to MLB’s own measurement data, changes in size and weight since 2014 are negligible taken together, so they cannot be responsible for an increased carry of almost 5 feet. So surface characteristics must be the cause. Unless I am missing something (not being an expert on the aerodynamics of a baseball, by any means).
By the way, how come you didn’t cite this article in the references:
https://www.theringer.com/2017/6/14/16044264/2017-mlb-home-run-spike-juiced-ball-testing-reveal-155cd21108bc
Isn’t that THE seminal article on how the actual measured changes in the ball (by MLB and by me) might affect batted ball distances?
The article by Ben Lindbergh you cited was about the ridiculous (and dishonest) denial by MLB that changes in the ball caused or significantly contributed to the HR and scoring surge.
My apologies to you and Ben. I meant to cite that article but instead cited a different Ringer article by Ben. My bad. And you are right that that IS the seminar article.
I am completely agnostic as to the reason for the change in carry. The analysis technique essentially says that the combination Cd*A/m has changed (since the effect of drag comes in that combination of factors). Not possible without additional information to untangle further.
This is fixed now. I’ll take responsibility for that mix-up. Although it’s partially Ben’s fault that he writes so many wonderful articles. 🙂
I should add that it is possible that an internal change could affect the aerodynamics of the ball, I think. That seems unlikely.
Thanks for this very interesting work and clear presentation.
I continue to take issue with those who trace the surge to the 2015 2nd half. (Not saying that’s your position, but it’s semi-implied by your starting points.)
Here are simple HR rates per batted ball (excluding sac bunts), by season half, since 2012:
Year – Half … HR% of batted balls
2012 – 1st Half … 3.77%
2012 – 2nd Half … 3.82%
2013 – 1st Half … 3.68%
2013 – 2nd Half … 3.41%
2014 – 1st Half … 3.32%
2014 – 2nd Half … 3.12%
2015 – 1st Half … 3.56%
2015 – 2nd Half … 4.08%
2016 – 1st Half … 4.38%
2016 – 2nd Half … 4.40%
2017 – 1st Half … 4.83%
2017 – 2nd Half … 4.99%
So, a pretty steady decline through the end of 2014.
Then a significant rise in the FIRST half of 2015, with continual rises ever since.
I just don’t see anything special about the 2015 2nd half, viewed in context of the years before and after.
Thanks for posting these interesting data. Assuming that MLB only changed the ball once, and it occurred before the 2015 season, it’s pretty amazing to see a jump from 3.56% (1st half 2015) to 4.83% (1st half 2017).
This begs the question: did they change the ball multiple times, or is that 36% two-year increase strictly due to batters adjusting their approach (plus whatever small contributions exist from natural variance and changes in relative batter talent levels, etc.)?
And what are they going to do if the HR keeps rising to, say 6%? Perhaps I am crotchety old purist, but I don’t particularly enjoy baseball with massive HR inflation.
I don’t know anything about MLB’s ball supply, but isn’t it possible that they changed the ball during the 2014-2015 offseason, and then it took time for the new balls to replace the old balls in the supply chain? Such that there were two different types of balls in circulation during the 2015 season, with the new balls gradually phasing out the old balls?
I love this! I do have one question about this conclusion: “We find the post-All-Star Game result for 2015 is intermediate between the pre-All-Star Game and the 2016 results, suggesting the transition between “high-drag” and “low-drag” baseballs occurred gradually following the All-Star Game.”
Couldn’t it instead suggest that there was a sudden change between “high-drag” and “low-drag” at some point around, say, late-August or early-September 2015?
Sure, your scenario is also a possible conclusion, but probably not likely given production, delivery, and usage schedules.