The Net Value of Draft Picks

It’s rare that a second-round pick becomes as productive as Yovani Gallardo (via Steven Paluch).
Yesterday, we tackled the total value of each draft pick, and how that has changed since the last studies on the subject. Today, we’re going to get into the net value that each draft pick produces, and how that affected the last free-agent class.
How Much Net Value Does Each Draft Pick Produce?
To determine a pick’s net value, we need to know how much that player will cost, and how much that same production would cost on the free agent market. There are a lot of moving parts here, such as the ever-increasing cost of a win and salary changes for pre-arbitration players, so we’ll keep things as simple as possible.
There are four key costs to consider for a player who is drafted:
- Signing bonus: For our purposes, we will assume that each draft pick receives the full assigned value for his pick.
- Pre-arbitration salary: The major-league minimum salary is currently $480,000, so we’ll assume that each player will make $1.5 million before he becomes eligible for arbitration. However, since the 25-man roster spot occupied by the draft pick will cost at least the major-league minimum, even for a replacement player who provides no real value, this money will not be included in a player’s cost.
- Arbitration salary: How much a player makes in his arbitration-eligible years.
- Minor leagues: Minor leaguers barely make any money, and the player development infrastructure is already in place, so we’ll ignore any cost here.
The first two are pretty straightforward, so all that’s left is to calculate the average arbitration salaries for each pick. While arbitration salaries can be projected quite accurately when you have a player’s numbers, we’re trying to make more general projections for draft picks.
One strategy would be to project a player’s salary by determining the relationship between arbitration salaries and the free-agent market. For example, if we know that a first-time arbitration-eligible player generally makes 35 percent of his market value, and know the average production for each draft pick and the cost of a win on the free-agent market, we can project his salary.
Nate Silver looked into this in 2005. His research was based on findings that arbitration-eligible players earned an average of 44 percent, 61 percent and 64 percent of their market value.
To see whether arbitration salaries have changed with respect to the free market, I looked at all players who have gone through arbitration over the past three years – more than 200 unique players – and calculated their salaries as a percentage of market value:
| Percent of Market Value, by Trip Through Arbitration | |||
|---|---|---|---|
| Position | Arb 1 | Arb 2 | Arb 3 |
| Hitter | 22% | 32% | 40% |
| Starter | 26% | 35% | 70% |
| Reliever | 52% | 80% | 143% |
| All Players | 28% | 37% | 62% |
It’s not surprising that relievers get paid the most relative to the WAR they produce, but we also know that relievers make more money in free agency than we would expect based on WAR alone. Because we’re not assuming a given position for the player drafted, we’re really interested in the total for all players. And the last few years have shown that players are making less money relative to their free-market value than they were a decade ago.
While this type of analysis is useful, it’s important to keep in mind that players are paid based on their past, and not expected, performance. If we look at 84 players who recently went through the arbitration process at least twice, we see a significant correlation between the first arbitration salary and total pre-arbitration WAR (r = 0.76). Meanwhile, the correlation to WAR produced in that same season was not reflective of the player’s salary (r = 0.39). Salary the second and third time through is based partly on performance in the most recent year, but the biggest factor is the previous year’s salary (r = .84 for years 1:2, and r = .89 for years 2:3).
We can use these numbers and perform a series of simple linear regressions to model arbitration salaries based entirely on WAR. By using the average value of a win over the time period of this sample (about $7 million), we can translate this number back into net value by WAR. While not everyone is compensated the same, this model works well enough to project average salaries for groups of players, which is the goal.
I decided to use arbitration costs exclusively (and not long-term extensions signed before free-agency) for two reasons. The first is that most players who are drafted don’t sign long-term extensions. When a team drafts a player, It is guaranteed his rights for only his first six-plus years in the majors.
The second reason is simplicity. If extensions were included, they would need to be accounted for on a case-by-case basis. This would be manageable for a few draft classes, but when you increase the scope to 15 seasons the amount of manual work becomes prohibitive. As this model accounts for only arbitration costs, it may slightly undervalue draft picks because it does not factor in the leverage that the team has in negotiating discounted long-term deals.
Let’s step back and see what we have so far.
Based on historical data, we can project average WAR per draft pick and the average cost of that player under his years of team control. And since recently, players haven’t experience a true peak but rather play evenly until they begin to decline, I assumed that WAR would be evenly distributed across all six team-controlled seasons.
We can use this information to project a net value for each draft pick. Before we bring the question of time into the picture, let’s chart the average expected value of the first 30 picks, using both methods of projecting arbitration salary (percentage of market for the method based on Nate Silver’s research, WAR for the WAR-based arbitration model discussed above).
| Net Draft Pick Value, Market % vs WAR-based Arbitration Model | ||||||
|---|---|---|---|---|---|---|
| Draft Pick | Pre-FA WAR | Market Value $ | Cost – Market % | Net $ – Market % | Cost – WAR | Net $ – WAR |
| 1-5 | 9.2 | 70.1 | 17.6 | 52.4 | 15.9 | 54.2 |
| 6-10 | 5.2 | 39.7 | 9.3 | 30.5 | 10.3 | 29.5 |
| 11-15 | 4.1 | 31.2 | 7.2 | 24.1 | 8.9 | 22.3 |
| 16-20 | 3.5 | 26.7 | 5.7 | 20.9 | 7.9 | 18.7 |
| 21-25 | 3.1 | 23.7 | 5.0 | 18.7 | 7.4 | 16.3 |
| 26-30 | 2.8 | 21.5 | 4.4 | 17.1 | 7.1 | 14.5 |
| 31-35 | 2.6 | 19.9 | 4.0 | 15.9 | 6.8 | 13.1 |
| 36-40 | 2.4 | 18.6 | 3.5 | 15.0 | 6.4 | 12.1 |
| 41-45 | 2.3 | 17.5 | 3.2 | 14.4 | 6.2 | 11.4 |
| 46-50 | 2.2 | 16.6 | 2.8 | 13.8 | 5.9 | 10.7 |
*The dollar cost listed is the total amount of money the player will earn above the major-league minimum; see above for explanation.
For the first five picks, the market percentage model actually projects a lower net value than the WAR model, although this quickly reverses itself and the differences become amplified, approaching a $3 million difference near the end of the first round. So which model does a better job at predicting actual arbitration costs?
The average top-five draft pick produces between six and 14 WAR under team control. Let’s look at some players who have fallen within this range and recently went through arbitration:
| Projected Arbitration Costs – Market % vs WAR-based Arbitration Model | ||||
|---|---|---|---|---|
| Player | Total WAR | Projected Arb $ – WAR | Projected Arb $ – Market % | Actual Arb $ |
| Kendrys Morales | 6.4 | 9.1 | 11.8 | 11.2 |
| Jarrod Saltalamacchia | 7.0 | 9.6 | 23.4 | 7.8 |
| Edinson Volquez | 7.0 | 9.6 | 4.5 | 9.6 |
| Nate Schierholtz | 7.1 | 9.6 | 9.3 | 8.6 |
| Carlos Gomez | 7.2 | 9.7 | 19.2 | 4.6 |
| Seth Smith | 8.1 | 10.4 | 6.8 | 10.6 |
| Jason Vargas | 8.2 | 10.5 | 12.7 | 15.8 |
| David Robertson | 8.6 | 10.8 | 11.9 | 9.9 |
| David Murphy | 10.3 | 12.1 | 13.1 | 11.8 |
| Luke Hochevar | 10.6 | 12.4 | 10.5 | 13.3 |
| Phil Hughes | 10.9 | 12.6 | 12.8 | 13.1 |
| Jed Lowrie | 12.3 | 13.6 | 26.0 | 8.8 |
| Average | 8.6 | 10.8 | 13.5 | 10.4 |
As you can see, the WAR model has the upper hand for this type of player, especially when the player has a breakout season in his final year of arbitration (as Gomez and Saltalamacchia recently did). For all players who have gone through three rounds of arbitration in the past five years, the WAR model has a higher correlation to actual salaries than the market percentage model — R2 values of 0.70 and 0.53, respectively (an average of Steamer and ZiPS projections was used to estimate WAR for players entering their final year of arbitration in 2014).
At the other end of the spectrum, we don’t find quite as many examples. Let’s look at the 55th pick, which will produce an average of 2.05 WAR. The market percentage model projects $3 million in arbitration, for a net value of $11.8 million, while the WAR model projects $6.2 million in arbitration for a net value of $8.6 million.
Recent players who totaled around 2.05 WAR under team control have mostly been relievers, such as Boone Logan (2.0 WAR) and Joe Smith (2.2 WAR), who received $5.8 million and $6.2 million in arbitration respectively. While the WAR-based arbitration does a better job of projecting actual arbitration salaries, the lack of players in this range shows its limitations.
When we calculate net value from a model like this, we’re treating a second-round draft pick as though it always turns into Boone Logan. In fact, 85-90 percent of the time it turns into nothing, but the rest of the time you get a player like Seth Smith (50th pick in 2004), Yovani Gallardo (46th pick in 2004) or even the occasional Joey Votto (44th pick in 2002).
Players who are roughly league-average or better (at least 1.5 WAR/season) make roughly 30 percent of their market value during arbitration. On the other hand, the borderline major leaguers – think Jerome Williams, Garrett Jones or Daniel Descalso – get paid closer to 60 percent of their market value (even when removing relievers from the group). In other words, because there is a salary floor, this model will have some issues when calculating the value of later draft picks, since less valuable players get paid more relative their market value than players who are league-average or better.
Improving the Net Value Model
The good news is that we can adjust this model by including only players who clearly belong in the major leagues. For example, only 15 percent of players drafted in picks 41-50 will actually total three or more WAR before they hit free agency, and those players produce an average of 12.6 WAR. Instead of looking at these picks as averaging a 2.2 WAR player, we need to imagine it as a lottery ticket giving the team a 15 percent chance of getting a 12.6 WAR player and roughly $74 million of net value.
For reference, these are the odds that a given draft pick will stick around in the majors (three-plus WAR under team control) or become something resembling a league-average player, or better (10+ WAR).
| Odds of Drafting Major League Contributor, by Draft Pick | ||||
|---|---|---|---|---|
| Draft Pick | Chance of 10+ WAR Player | Chance of 3+ WAR Player | ||
| 1-5 | 35% | 55% | ||
| 6-10 | 25% | 43% | ||
| 11-15 | 23% | 41% | ||
| 16-20 | 17% | 32% | ||
| 21-30 | 11% | 23% | ||
| 31-40 | 7% | 15% | ||
| 41-50 | 7% | 15% | ||
What we did above was use the historical data to project average WAR, and then calculate net value using this projection. Alternatively, since the WAR-based arbitration model is better suited for individual players instead of groups, we can apply it to each individual draft pick from our 1991-2005 data set.
Doing this allows us to include the actual cost of the draft pick, but not major league salaries and arbitration costs, for players who never become regular contributors at the major league level. Doing so gives us the following model:
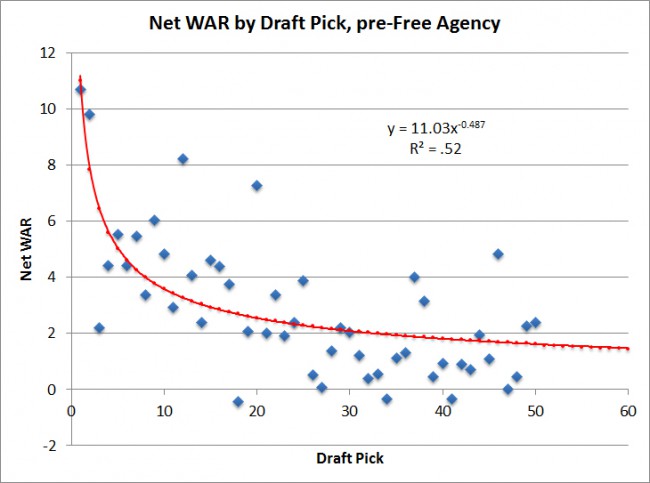
This graph looks quite a bit like the one shown earlier depicting total WAR under team control. The main difference is the coefficient (11.0 versus 14.1), which tells you that for the earlier picks, about 78 percent of a drafted player’s total WAR under team control is net value for the team.
Put another way, when a draftee turns into a major league player (at least 0.5 WAR/year), he will earn roughly 22 percent of his market value before hitting free agency (on top of the major-league minimum).
Based on this model, let’s look at the actual net savings, in both WAR and dollars, for each group of draft picks. (Total WAR shown is from the 1991-2005 regression, as the associated values are based off of the same data set.)
| Net Draft Pick Value – Modified Regression | ||||
|---|---|---|---|---|
| Draft Pick | Average WAR | Market Value | Net WAR | Net $ (2014) |
| 1-5 | 9.2 | 64.6 | 7.2 | 54.7 |
| 6-10 | 5.2 | 36.6 | 4.1 | 30.8 |
| 11-15 | 4.1 | 28.8 | 3.2 | 24.1 |
| 16-20 | 3.5 | 24.6 | 2.7 | 20.6 |
| 21-25 | 3.1 | 21.8 | 2.4 | 18.2 |
| 26-30 | 2.8 | 19.8 | 2.2 | 16.6 |
| 31-35 | 2.6 | 18.3 | 2.0 | 15.3 |
| 36-40 | 2.4 | 17.1 | 1.9 | 14.3 |
| 41-45 | 2.3 | 16.1 | 1.8 | 13.4 |
| 46-50 | 2.2 | 15.3 | 1.7 | 12.7 |
These numbers are actually fairly close to those that we calculated using percent of market value, once you adjust for the inclusion of the major league minimum earlier.
If these numbers seem a bit high, they should, because there’s still one more thing we need to adjust for.
How to Value Future WAR
A bird in the hand is worth two in the bush.
When it comes to money, now is always better. Matt Swartz did a great job of explaining how baseball transactions are investments. Money buys players, players earn wins, and win puts fans in the seats with team jerseys on their backs, bringing money back to the owners. The circle of life.
With this in mind, it’s not a surprise that teams place a discounted value on future wins. Sure, there may be some exceptions. Teams like the Astros and Cubs would almost certainly borrow a few wins from 2014 if they were allowed to count toward future seasons. However, across the majority of baseball, sooner is better.
Nate Silver estimated a five percent discount on value for future seasons and Matt Swartz has estimated it to be 10 percent annually, a figure I will use here.
One way to account for this is to simply discount the total value in one shot. The average player reaches the majors around three years after being drafted, so his team-control years in which he produces value are three to nine after the draft. If you apply the discount to the average of six years after the draft, you can simply subtract 47 percent (0.9^6 = 0.53) from the average value.
However, there’s another factor to consider, which is where the value is coming. A disproportionate amount of a player’s net value is accrued in the first three years under team control when salary is at its lowest. This is also where the future discount should apply the least.
Therefore, when we factor in the future discount by each individual season of team control, the draft pick should appear more valuable. Here’s what we get:
| Net WAR, with future discount applied | |||
|---|---|---|---|
| Draft Pick | No Discount | Year-by-Year | Six-year Average |
| 1-5 | 7.2 | 3.4 | 3.8 |
| 6-10 | 4.1 | 1.9 | 2.2 |
| 11-15 | 3.2 | 1.5 | 1.7 |
| 16-20 | 2.7 | 1.3 | 1.4 |
| 21-25 | 2.4 | 1.1 | 1.3 |
| 26-30 | 2.2 | 1.0 | 1.2 |
| 31-35 | 2.0 | 0.9 | 1.1 |
| 36-40 | 1.9 | 0.9 | 1.0 |
| 41-45 | 1.8 | 0.8 | 0.9 |
| 46-50 | 1.7 | 0.8 | 0.9 |
Not only do we not see a big difference, but the year-by-year calculation actually further devalues the draft picks. The reason is that there is a significant increase in net WAR over the first few years of team control. However, this benefit is more than offset by the fact that one of the biggest payments from the team’s side – the signing bonus – is paid up front.
Regardless of how you apply the discount, this table illustrates how much this affects a draft pick’s value. For example, a pick in the 26-30 range (like the one the Braves gave up for Ervin Santana) appears to be worth around $16.6 million in today’s dollars. However, when you account for the fact that the pick won’t produce any value for years to come, the value drops more than 50 percent to $8.1 million.
The same draft picks would be worth $10.9 million if you were to assume just a five percent annual discount for future WAR (as Silver did). I’m not an economist, so I’ll yield to Matt Swartz who is much more qualified to measure the future value of major league wins, as he has in the past. This point merely illustrates how a team building for a few years down the road that might not discount future WAR quite as much can end up with a very different draft pick valuation.
References & Resources
- WAR figures for draft picks from 1991-2005 are from Baseball-Reference’s draft tool.
- WAR figures for recent arbitration-eligible players are from FanGraphs.
- Arbitration salaries are from Baseball-Reference and Cot’s Baseball Contracts.
Good work. One thing to consider with Santana and the Braves is that he was signed early enough that they can put another QO on him after the season. Not 100% – injury or a slump could make that an unappealing option, but they stand a decent chance of getting a draft pick back.
This is true (and was actually raised in the comments section of the first article as well). While it doesn’t change the actual value of the draft pick that the Braves gave up (or might receive), it should certainly be factored into how we evaluate the signing.
Great work. One of the confounding problems though is that for the time period in this dataset, the slotting system had not yet been implemented. In many cases, where a player was drafted (especially at the granularity you are comparing) was as much a function of his perceived bonus demands or signability as it was his talent, and no-signs were much more common. These concerns are still around in the slotting system, but they are much diminished. If the historical signing bonus numbers could be found, it might be interesting to run these calculations by ranking players 1 to 50 by signing bonus rather than by draft spot. Going forward one would think top level talent is less likely to fall in draft spot due to money issues than during the time period covered here
You are 100% correct, there are certainly a number of players that slipped due to concerns about signing bonuses – take Derek Jeter who slipped to sixth in 1992 for example. This could mean that under the current draft restrictions, the slope should be a bit steeper, as the “best” players should always go near the top of the draft, and fewer of them will slide into the teens or twenties.
I hadn’t thought about ordering picks by signing bonus, and I would be very interested in seeing what the resulting regression looked like for that. However, this would assume that teams would always have preferred the higher paid player. In cases like 2005, where Mike Pelfrey (9th) signed for more than Ryan Zimmerman or Ryan Braun (4th/5th), you run into some issues, and I’m not sure that this would give you a more accurate picture.
The best way might to go through and cherry pick players who clearly dropped because of signability concerns. A quick look from 2001-2005, I’m only seeing a few guys who signed conspicuously above their slot and went on to have productive careers – Guthrie and Francoeur in 2002: http://www.baseballamerica.com/today/draft/top100sign02.html
As I mentioned, this would certainly affect the trend, but from looking at the numbers, I’m not sure how much of a difference it would make.
You’re probably correct that it would only affect the results marginally, but going with just that draft class, other players that would have moved into higher buckets would include Cole Hamels (from 15-20 to 11-15) Scott Kazmir(11-15 to 5-10), and Jon Lester (none to 36-40). Given that the average WAR totals are dependent on the comparatively small number of players who make it, it may well make a difference
Out of curiosity, how did you handle the no-signs? Did you average in the zeros or remove them from the data set entirely?
You’re right, it might make a difference. However, I’m not really comfortable making a judgment call on where players “should have” gone though, so this is simply one of the limitations of this study.
I actually hadn’t factored in players who never signed since I had trouble finding a reliable source of year-to-year signing data, thanks for bringing this up. Looking through now, there aren’t a ton of no-signs in the top-50. Here’s the list from 2001-2005:
2005: Hochevar
2004: Wade Townsend
2002: John Mayberry and Micah Owings
2001: Jeremy Sowers and Alan Horne
Owings led the group with 4 WAR under team control.
There were a few guys in the 90s, however, who failed to sign and went on to have productive careers (Mark Prior, JD Drew). I re-ran the regression with the updated numbers and it ends up decreasing the net WAR value, but outside of the top-10 picks the difference is less than a tenth of a win.
The payoff is not a fixed dollar amount that is discounted but a win. The value of the win is increasing over time so you cannot apply a standard discount argument here. At the same time, you are not accounting for risk or uncertainty at all.
You have a $1 million dollar lottery ticket that may pay out nothing 99% of the time, and will pay out $100 million 1% of the time. The obvious point is that you will pay less than $1 million for this ticket because you are risk averse. The less obvious, but dominant point, is that you are making a huge payout on an assumption of perfect certainty about the far tail of a distribution you don’t really know much about.
Maybe the payout is nothing 99.9% of the time and $2 million .01% of the time. Can you really say with certainty what the distribution of talent will be? Exactly how stable are these distributions across time periods, and why do you think the future will be exactly like the past? When real money is on the line, it’s not enough to pretend that you know what the distribution is.
In many cases, you focus on the mean and ignore the tail. The draft is an example of a distribution where the mean has no value and the payoff is only in the tail end of the distribution. How one can assign a value to that is not really well understood — perhaps you can propose some approaches, but this issue isn’t dealt anywhere with your calculations.
Thanks for the thoughtful response.
As far as the discount, I’m not an economist, so I’m not the best person to answer a question. The discount being applied isn’t in terms of money/inflation, but the delayed opportunity to re-invest in the on-field product. The increasing cost of a win (and increasing arbitration cost) are factored into the initial net WAR calculation. But when it comes to a win this year versus a win three, four, or eight years in the future, you need to account for the relationship between the the quality of the team (the product) and the tickets/merchandise/viewership (revenue). If you can have a good team now versus in six years, you’d rather have it now, because then you’ll be bringing in more revenue for the next six years. Obviously this isn’t black and white when it comes to baseball, as wins have different values to different teams depending on their market and their position in a win curve, but this is a best estimate of how future wins are valued by the MLB as a whole.
You are correct that I didn’t account for risk. Every team would probably take $5M in cash rather than a 5% chance at winning $100M. If you have any good way to account for this risk, I’m open to suggestions.
I do understand that it’s difficult to really determine how talent is distributed given the huge amount of variability in the draft. It’s tough to be certain, but the fact that the 15-year sample I looked at showed similar trends to Sky’s more extensive analysis gives me some confidence in the model. There’s always going to be a huge amount of uncertainty, but that doesn’t mean that we shouldn’t try to make our best estimate at how the talent and associated value are distributed throughout the draft based on the data that we have.
I’m trying to understand your last question. Yes, after the first two picks, the odds are that you’re paying a few million dollars for nothing. However, the way I applied the net value model to individual players, is equivalent to calculating the success rate and value of a successful pick for each draft pick.
For example, for the first pick, 9/15 picks have posted at least 10 WAR under team control, and those players have averaged 22 WAR for a net value of 17.7 wins, multiplied by the 60% success rate gives you 10.6 net WAR. Perhaps it would be more informative to illustrate probability of certain quality players in different pick ranges, but that wouldn’t help you try to estimate how much a given draft pick is worth.
Accounting for risk is difficult. In economics/finance, you would convert this:
Expected Return = p(A)*A + p(B)*B
To this:
Utility of Return = p(A)*u(A) + p(B)*u(B)
Where u is a strictly concave function. Then, Jensen’s inequality will mean that a 100% chance of $1 is worth more than a 10% chance of $5.50 and a 90% chance of 0.5
However, the underlying rationale for this is diminishing returns, in that you do not get twice the utility from twice the gain. It’s not clear that this is the case in baseball — e.g. would a team rather have three 2WAR players or one 6 WAR player? In any case, the above mathematical model does not fit the data well, in terms of describing observed risk aversion either in surveys nor in observed risk premia in the capital markets. But if you do this, at least you will be following standard practice for taking risk into account. There may be other approaches — this is the crux of the matter, IMO.
For uncertainty, you need to make the case that previous draft outcomes do a good job of describing future draft outcomes. Normally this is an acceptable assumption but here the value of the draft is coming from the tail — from just a handful of players. Now, you are really on shaking ground because you are saying that the probability of getting another A-Rod is exactly the same every year — say one in 40 for a first round pick. And not, for example, 1 in 50 or 1 in 30. Whether it is one of these other cases makes a big difference on the value of the first pick. Here, there is body of knowledge called extreme likelihood theory that, in principle, could be used but what is going to sink this approach is that you have such a small sample size to work with. The combination of small data set and reliance on the tail end of the distribution to determine overall value puts any analysis of the type presented here on very shaky ground.
A completely different approach would be to look at other sports where draft picks can be sold or traded, and observe the inferred market price for the pic.
Robert,
You’re missing a few things.
1) As Matthew mentioned but I’d like to highlight further, future wins should be heavily discounted for the simple reason that winning is valuable because it creates brand value. In practical terms, this often means that playoff appearances encourage people to buy season tickets– the sooner that they buy them, the better. Winning sooner is better because you get money earlier from doing so, and because you build brand earlier that persists into the future. One of the single biggest predictors of what team someone is a fan of is if a team in their area won a World Series when they were about 8 years old or so. Those people tend to stay loyal to their hometown team as adults, even as they move away from their area or even as other nearby teams are successful.
2) Teams should not be risk averse. In fact, quite the opposite. Would you rather have a team that you knew would win 80 games or that would have a 50/50 shot of 65 wins or 95 wins? The team with higher variance in their expected number of wins has a higher probability of making the playoffs, which is where the money is. It’s considerably more valuable. Teams should not be risk averse at all and don’t behave as though they are in terms of expenditures.
3) The reason that Sky Andrecheck’s model is so useful is that it doesn’t focus on the tails. It smooths the expected value in a continuous fashion so that if a team had a 50 WAR player with the 18th pick, it doesn’t make the 18th pick more valuable than the 17th or 19th. It smooths the expected value out. Matthew’s work does an excellent job of showing that the shape of the curve may change. But the fact that it’s smoothed over a larger sample of picks means that flukey tails aren’t driving the distribution.
How did you estimate market value? Since arbitration awards are essentially 1 year contracts (slightly worse given team options to cancel in spring training) they are not directly comparable to average annual values of long term contracts, which are clearly discounted for team risk/player security value.
Typical discount rates are the “risk free” returns easily available in other investments, essentially the “replacement level” investments. Baseball teams don’t typically have other players easily available at “market cost”, so that’s a reason MLB discount rates should be higher than investment discount rates. Another reason they are likely far higher (but shouldn’t be) is that GMs typically have relatively short tenures. They are heavily incented/biased to over-discount future wins now, especially wins that would occur after their current contract, and overvalue current season wins, especially if near a contract extension.
Matthew, you really did an excellent job in this article. I really am impressed by all of the detail. You found some amazing stuff. I think that I’ll need to update some of my work on $/WAR based on your findings. You have some very interesting findings.
Something that is worth noting is that the 10% discount rule might need to be re-estimated. The way that I found the 10% discount is that I looked at players who had draft pick compensation attached and those that didn’t, and kept adjusting the discount factor on the future WAR until it worked out. So I think the value of the draft pick will come back down from what you estimate, but only because the discount rate is higher. I think you’ve absolutely identified some changes that could improve things. Even if the average pick is higher, I suspect your work will change how I’d value earlier vs. later picks than average.
Great work!
Thanks a lot, glad you enjoyed the article!
Interesting that Dan Szymborski said that he only discounts 4% annually, it feels like this is the area where the biggest discrepancy in draft pick values exists (and is the most difficult to accurately determine).
Interesting. It could be that 4% is normative and my 10% is positive (descriptive). Teams may discount the future more than they should. In practice, they act as though 10% is the correct discount factor according to my research. I think that probably the best justification for 10% being normative as well is that team valuations tend to grow closer to 10% annually, which suggests that the internal rate of return may be very high to investments in a club making it very valuable to get revenue earlier. However, 4% is a more accurate description of regular market returns as well as human utility– people tend to value being happier now only a few percent more than being happier next year. In $/WAR analysis, I lean towards describing behavior rather than justifying it, but obviously using WAR (or superb draft pick modeling like your own) ends up being normative in a way too.
It could have something to do with the fact that the GM isn’t guaranteed to still be around by the time a good draft pick eventually pays off.
FIFA World Cup 2014 Opening Ceremony Live Stream, Any time FIFA in October 2011 given Brazil’s productive business center Sao Paulo as the Planet Cup’s cracking open match up location, these people did not that is amazing 11 times prior to kickoff this ground may not …