The Physics of a Rising Fastball

It isn’t surprising to see Aroldis Chapman’s fastball has the most “rise” to it. (via Keith Allison)
It appears as though the legend of the rising fastball has actually been debunked. Baseball analysts now talk about “apparent rise” or “what rise looks like.” Even “MythBusters” has described the rising fastball as “busted.”
That said, Alan Nathan pointed out, “A fastball could rise in principle. It could actually rise if you could get enough spin on it.” The point here is to investigate just exactly how much spin is needed. Unfortunately, it will require a bit of physics – so, try to stay awake for the next few paragraphs, OK?
To simplify matters, let’s just think about the two forces that act vertically on a pitch in flight. The first is pretty easy to understand – gravity pulls the ball downward toward Earth. This is the weight of the ball which is established by MLB.
Rule 1.09 – “The ball shall be a sphere formed by yarn wound around a small core of cork, rubber or similar material, covered with two strips of white horsehide or cowhide, tightly stitched together. It shall weigh not less than five nor more than 5¼ ounces avoirdupois and measure not less than nine nor more than 9¼ inches in circumference.”
For the rest of this article, we’ll take the middle road and use five and one eighth ounces which is 0.32 pounds for the downward force on a pitched ball. Now the upward force – this is more complicated.
The upward force on the ball is called the “Magnus force” or the “lift,” but that’s just a name. The Magnus force is caused by the air through which the ball is traveling. It is due to the interaction between the spin of the ball and said air. I’ve written in detail about the underlying cause of the force on a spinning ball previously, so I’ll spare you those details here.
The Magnus force is usually written as where CL is the “lift coefficient,” r is the density of the air, A is the cross-sectional area of the ball, and v is the speed of the ball. These quantities all seem pretty straight forward with the exception of the lift coefficient which is anything but easy to understand.
The lift coefficient is extremely complicated to actually figure out. It depends upon the speed of the ball and the backspin in a pretty complex way (see “The effect of spin on the flight of a baseball” by Alan Nathan). There is still some debate as to the exact relationship, but for those that care, here is the equation I used for the lift coefficient,

where w is the backspin in revolutions per minute (rpm) and v is the speed of the ball in miles per hour (mph).
To summarize, we can compare the size of the Magnus force which depends upon the speed and backspin on the ball to the weight of the ball. After all is said and done, if the upward Magnus force is greater than the downward weight of the ball, the ball will in fact rise. Otherwise, it will fall. So, the critical condition is when the two forces are equal.
When you set the two forces equal and do a bunch of “mathy” stuff, you get the equation below describing the relationship between the speed of the ball and the backspin of the ball when the forces balance,

where again, w is the backspin in rpm and v is the speed of the ball in mph. In the graph below, the relationship at the critical point is given by the dark blue curve. If the combination of backspin and velocity is above the curve in the blue shaded area, the ball will actually rise. If the combination is below the curve, the ball will fall.
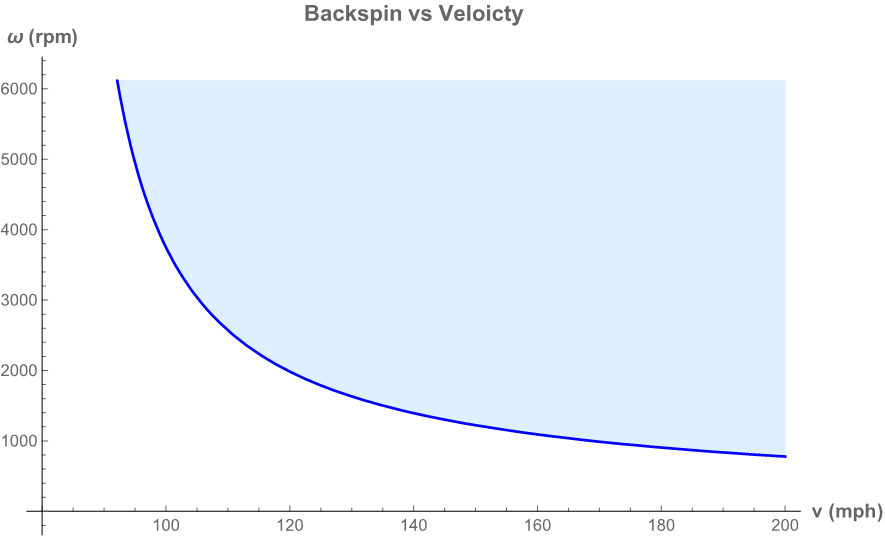
The graph has a couple interesting and pretty sensible features. When the speed drops too low, the required backspin gets impossibly large. In a similar way, as the spin rate gets small, the necessary velocity grows way too big. These features are consistent with the basic physics of the Magnus force which requires both speed and backspin to provide an upward force.
Now that all the pesky physics and math details are out of the way, we can finally have a bit of baseball fun. Let’s study a few fastballs and see how close they come to actually being able to rise. Of course, the ones we need to examine must have high velocity and high backspin. The pitch with the highest backspin is generally the four-seam fastball. Searching the PITCHf/x database for 2016 for four-seamers gives the table below listing the top 10 pitchers in terms of the number of pitches above 100 mph.
| PITCHER | PITCHES OVER 100 MPH | % OF PITCHES OVER 100 MPH |
|---|---|---|
| Aroldis Chapman | 526 | 54.12 |
| Mauricio Cabrera | 342 | 53.11 |
| Noah Syndergaard | 68 | 2.32 |
| Arquimedes Caminero | 50 | 4.54 |
| Brian Ellington | 43 | 7.61 |
| Nathan Eovaldi | 36 | 1.74 |
| Dellin Betances | 34 | 2.72 |
| Carlos Estevez | 34 | 3.32 |
| Joe Kelly | 23 | 3.11 |
| Bruce Rondon | 20 | 3.54 |
Numero uno is no surprise – Aroldis Chapman, who hurls over half his pitches above the century mark. In fact, Chapman threw 25 pitches over 104 mph! Mauricio Cabrera fired 52 between 102 and 103 mph. To see how close these guys are to throwing a truly rising fastball, let’s look at the following four scenarios.
| Graph Color | Pitcher | Min Speed | Max Speed | # Pit | Avg. Velo | Avg. Backspin |
|---|---|---|---|---|---|---|
| Gray | Aroldis Chapman | 104.0 | 105.1 | 25 | 104.4 | 2,360 |
| Blue | Mauricio Cabrera | 102.0 | 103.0 | 52 | 102.3 | 1,580 |
| Orange | Noah Syndergaard | 100.0 | 101.3 | 68 | 100.4 | 2,275 |
| Yellow | Arquimedes Caminero | 100.0 | 102.2 | 50 | 100.6 | 1,625 |
Plotting them on the backspin vs. velocity graph will give an indication of how close these fire-ballers are to making a fastball actually move upward. The color on the left of the table above corresponds to the data point on the graph.
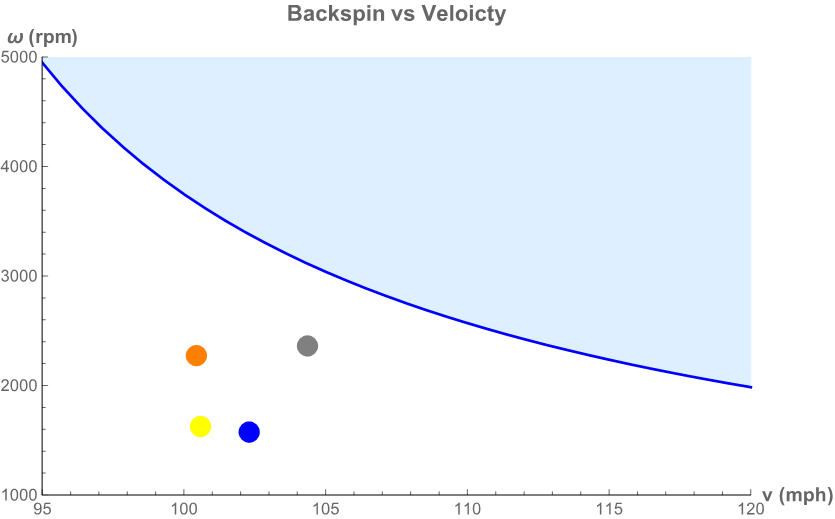
Using Chapman’s average speed and backspin, you can find the lift coefficient and then the Magnus force. I got 0.28 pounds for the Magnus force compared to the 0.32 pounds which is the weight of ball. In other words, Chapman is surprisingly close to being able to throw the mythical rising fastball.
To be fair, I am using the starting speed of his pitches and we need to remember pitches at this speed pitches slow down by eight to nine mph during their flight to the plate. So, the Magnus force I calculated is the maximum which occurs when the ball is released. The lift will drop about ten percent on the way to home.
So, what would Chapman have to add to his already superhuman fastball to make it rise? Looking at the horizontal dashed line in the graph it appears that with the same spin (2360rpm) Aroldis would need to throw the ball at 113 mph. If instead he can maintain the speed, the vertical dashed line shows he could spin the ball at a rate of 3100 rpm.
There are other possibilities that would include lesser increases in both velocity and backspin. However, it would seem that these are beyond human mechanical abilities. Nonetheless, as a friend of mine is prone to say, it is still nice to think about.

I wonder if some pitchers who throw a fastball at a more normal speed are still effective because their spin rates are higher than normal? Not that their ball rises, but that it doesn’t drop at the expected rate. Mets rookie reliever Paul Sewald comes to mind. His fastball is 2400 rpm, even though he only throws it at 92 mph.
Definitely. Hitter believe a ball “rises” because it falls less than they expected. We cannot, as humans, track the entire path of the ball, so our brain picks intervals to gauge the pitch track. This makes it possible for a ball to drop less than the hitter expected, and for him to swing over it.
Exactly. Well said.
Swing under it…
Viscous torque also slows down the spin of the ball while in flight. Formula is 8 * pi * (ball radius)^3 * viscosity * spin rate. So for fringe cases the ball may start out as a rise-ball, then drop again.
True if the distance was long enough, but we’re talking 66′ in baseball and 43′ in softball at speeds of 100mph and 70 mph. No time for mid-course corrections. The ball gets there in 3ms.
Is there any way for anything to “rise” other than “up?”
Depends on your perspective, probably. 🙂
Fun stuff — maybe someone could take a pitching machine and ramp up the spin of the ball enough to actually rise it — would be something to see!
Watch any women’s fastpitch. They can make it jump up in the right conditions.
Enjoyed the article, but I wonder, if people saw a fastball that had an upward bend but still always downward angle into the zone — because of its release point — is that “rising”?
I could see the argument either way, but I hear “rising” as “is it moving up when you swing at it” (rather than moving down while accelerating up).
Might also be fun to work through the requirements for a “moving up” fastball from a submariner.
Maybe from the POV of utility, the physics is telling where it best to pick up the FB from a guy like Chapman. Someone should ask Buster Posey. He, at one time, was hitting over .500 against him.
Kagan leaves an important factor out…baseball pitchers are pitching down to the batter. This means the spin on the ball has to overcome the downwords angle of the pitch. At best, the ball would end up coming in flat, which might look like it rises because it’s higher than the batter expects.
A rise ball is very clearly possible in fast-pitch softball. The pitcher releases the ball as low a possible, often with an upward vector and the spin pushes the ball farther up. I know, I had a great rise and pitched in two national men’s tournaments.
It’s not just the Magnus force. You have to consider the angle of the ball at release
Who gets the most spin in MLB on their 4-seam fastball? How close would Chapman be if he threw 105 mph with the same spin as the spinniest pitcher in baseball?
The above “duly noted”. But how in the hell does the ball look as though it’s rising on television, but only for certain pitchers. It’s not coming at the viewer to cause “neural overload. It never happens for pitchers who throw “slop”. So if the viewer can actually see the ball rise relative to a straight line behind and alongside, why then does the ball seem to rise? Maybe “some of us” have brain refresh rates higher than others 😉
Compared to baseballs, underhanded fast pitch softballs are thrown slower, have a lower spin rate, and are heavier. The absolutely do NOT “Rise”. The softball can follow the upward path in which is was thrown, but that is not the same thing. The baseball mound verses the flat mound of softball is irrelevant to having a ball deviate upward from its initial trajectory. Of course, to your point, to actually have a baseball rise while being thrown at a downward angle from a mound seem to be more difficult. Though again, I repeat, there is not such thing as an actual rise ball thrown by a human in softball. It has been completely debunked by science.
I think the subject is interesting but I’m not a physicist. I can’t understand this stuff. Can someone tell me if his conclusion is that it is or is not possible for a fastball to rise. I always heard it was physically impossible. I always thought that the appearance of “rising” was an optical illusion caused by the pitcher throwing off a mound.
I don’t know anything about lift coefficient. Can someone just translate this into English?
Four missing factors:
1) Mound height, as others noted.
2) Height of release point, ditto. Not from the mound but from field level, or to be precise, from the plate.
3) Air density. Mentioned in the intro but not in the formulas. Does it vary enough to have an impact (a) at a single location because of meteorological conditions, such as humidity, or (b) by height above sea level, e.g. Colorado vs Baltimore?
4) Wind speed & direction. The formulas assume none, and rightly so. But would a tailwind help keep the ball up?
I wonder if you could have wind actually pushing the ball upwards. Wind in a ballpark is swirling around as it comes up and over the facade of the stadium…
Seems like a ball traveling 100 mph over 60’6″ would maintain enough energy/velocity to continue on an upward trajectory or even rise. External ballistics, trajectories graphing and ballistic coefficients. It’s proven that curve balls curve…but apparently can’t maintain an upward trajectory.