The Physics of the Pop-Up

Despite looking up, Shin-Soo Choo did not hit any pop-ups this season. (via Keith Allison)
It’s late in the game, and your team is finally showing some signs of life. The tying runs are in scoring position with two down, and that brash young rookie is coming up to the plate. For the first time in weeks, the home crowd is buzzing with anticipation. From the mound comes the high heat, and that stupid rookie can’t resist the excitement of the moment. He swings and pops it up. The air gets sucked out of the building in the time it takes the ball to gently land in the shortstop’s mitt. Now that the game is over and you have nothing better to do, let’s look at the physics of that infernal pop-up.
From high school you might remember Galileo’s Law of Falling Bodies, “All objects near the surface of Earth accelerate downward with the same acceleration of 9.8 m/s2.” You don’t remember that? Maybe you were just “high in school” instead of “in high school,” or maybe you were just sick that day. In any case, the point is the acceleration—the change in velocity—is that same when the ball is heading upward as when it descends. The result, as your crazy-haired physics teacher told you, is the ball will be caught by the shortstop as the same speed it left the bat.
Maybe that’s why you never paid any attention in physics class. Mr. Crazyhair’s statement is ridiculous! You’ve caught half a million pop-ups, and there is no way that they hit your glove at the same speed as a line drive. They are always going slower. The missing idea is that Galileo’s Law only applies if air resistance is very small—not the case for a baseball moving at game speeds.
 Air resistance, or air drag, is always opposite to the motion. When the pop-up is rising as in Figure A, the air drag is downward, slowing the ball down. Therefore, it won’t reach the height predicted by Galileo or your physics teacher.
Air resistance, or air drag, is always opposite to the motion. When the pop-up is rising as in Figure A, the air drag is downward, slowing the ball down. Therefore, it won’t reach the height predicted by Galileo or your physics teacher.
Once the ball reaches its maximum height, it begins to fall downward as in Figure B. The air drag acts against this motion also, so the ball doesn’t speed up as fast as Mr. Crazyhair predicted. All in all then, the ball will be moving much more slowly when it is caught than when it left the bat.
What about the path of the ball through the air? Your teacher told you it was a beautifully symmetric parabola that looks the same as the ball rises as when it falls. This is also wrong. The path of a pop-up can be quite asymmetrical due to the interaction between the ball and the air.
Here’s a pop-quiz or maybe a “pop-up” quiz. Question 1: Which way is the top of the ball spinning when a pop-up leaves the bat?
(a)toward the backstop
(b)toward the outfield
(c)none of the above
(d)all of the above
 Did you pick answer a? In Figure C, the ball is heading toward the bat. Since the result will be a pop-up, the bottom half of the ball is going to collide with the top half of the bat. Figure D shows the initial contact.
Did you pick answer a? In Figure C, the ball is heading toward the bat. Since the result will be a pop-up, the bottom half of the ball is going to collide with the top half of the bat. Figure D shows the initial contact.
You can see that since the middle of the ball is still moving toward the catcher, the ball must rotate. The rotation has the top of the ball moving toward the backstop. In Figure E, we see the ball leaving the bat with the spin it has gained during the collision.
A spinning baseball does amazing things, as every good pitcher and frustrated hitter knows. The force exerted on the ball when it spins through the air is called the Magnus force. The topspin on a curveball creates a downward Magnus force, causing the ball to drop compared to the trajectory of a non-spinning ball. Similarly, the backspin on a fastball creates an upward Magnus force, causing the ball to drop less than a non-spinning ball.
Pop-up quiz Question 2: Looking at figure E, which way will the Magus force push a pop-up that is headed upward?
(a)mostly toward the backstop
(b)mostly toward the outfield
(c)none of the above
(d)all of the above
If you rotate your iPad 90˚ to the left, Figure E will look just like a curveball with topspin headed toward home. So, the Magnus force will be downward. Rotating your iPad back, that means the Magnus force will tend to push the pop-up mostly toward the backstop, answer a.
Pop-up quiz Question 3: Which way will the Magus force push on a pop-up that is headed downward?
(a)mostly toward the backstop
(b)mostly toward the outfield
(c)none of the above
(d)all of the above
This time, rotate your iPad to the right and the ball will look like a fastball with backspin. The force will be mostly toward the outfield, answer b. So, while the ball is headed upward, it will move a bit back toward the backstop. Once it reaches the top and begins to head downward, it feels a force toward the outfield. Alan Nathan, noted baseball physicist, was the first to realize that if the spin was sufficiently large, the ball might be able to do a loop-de-loop which he called a “paradoxical pop-up.”
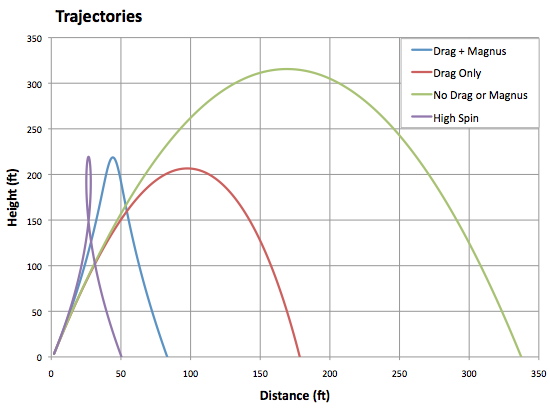 A picture is worth a thousand words, so as a summary, the sketch above shows the trajectories of four pop-ups all launched at 100 mph at a 75-degree angle. The data were generated by Alan Nathan’s Trajectory Calculator. Your physics teacher’s pop-up (green) is beautifully symmetric. The ball rises just the same way it falls. But look where it falls…it’s practically a homer. Sorry, Mr. Crazyhair, your pop-up just isn’t realistic.
A picture is worth a thousand words, so as a summary, the sketch above shows the trajectories of four pop-ups all launched at 100 mph at a 75-degree angle. The data were generated by Alan Nathan’s Trajectory Calculator. Your physics teacher’s pop-up (green) is beautifully symmetric. The ball rises just the same way it falls. But look where it falls…it’s practically a homer. Sorry, Mr. Crazyhair, your pop-up just isn’t realistic.
Adding in the air drag (red) gives a trajectory where the ball goes about 100 feet horizontally during rise but only about 75 feet during the fall. The symmetry is gone, but the ball lands in the outfield, which isn’t really right, either. Including air drag and Magnus force (blue) gives a pretty realistic pop-up coming down in the infield. You can see the effect of the spin-created forces in the shape of the curve.
The first three trajectories all used a spin rate of 2000 rpm. For a probably unrealistic spin rate of 4000 rpm, we see a paradoxical pop-up (violet) doing a loop-de-loop. Now that you’re all studied up, you’ll be quite prepared for your next pop-up quiz!

The origin of my interest in this subject came from a class I taught on the physics of baseball back in the late 1990’s. One of my students was a former catcher, who told me that catcher’s are taught not to overcommit on high popups behind home plate, since the ball might loop back on the way down. It is amazing how often it happens that an infielder settles under a popup, then back-peddles at the last moment to make the catch.
Alan,
Your Trajectory Calculator is a great gift to all of us….DK
Catchers are also taught to turn around and face the backstop to catch a popup, even if it is in fair territory, recognizing that on the downward part of the trajectory the ball is curving away from the backstop, and you don’t want to wind looking like infielders do when they have to try to catch a ball with their back to home plate.