Why you can’t subtract FIP from ERA

Okay, so the title is misleading. They’re both numbers and can be subtracted from one another with wild abandon. Just don’t expect it to mean anything.

What do I mean? The basic formula for FIP is:

(13*HR+3*BB-2*K) / IP + 3.2

You can fancy it up a bit (or a whole lot, if you want something like tRA), but what you’re getting is still a linear model of run scoring. Which is fine, so long as you understand what that means.

Let’s take the home run term of that equation for a minute. It’s supposed to correspond with the number of runs allowed per home run. Here’s the thing, though. The number of runs allowed per home run goes down if you have a low walk rate or a high strikeout rate or both, because that means there will typically be fewer runners on base when a home run is hit. A linear model of run scoring doesn’t account for that.

What this means is that you have a much narrower band of results when you use FIP than when you look at ERA. To illustrate:

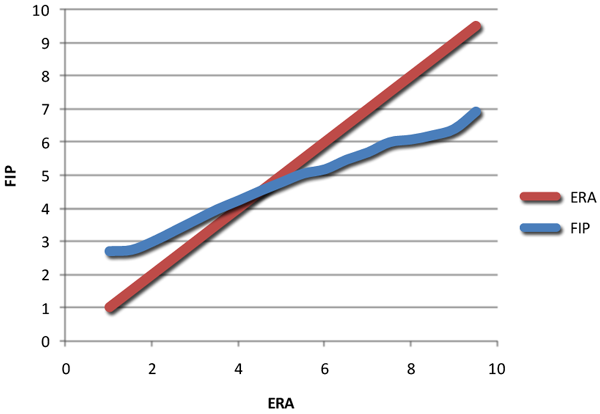
The red line represents ERA graphed against itself. As one can imagine, ERA has a one-to-one relationship with itself. The blue line represents FIP relative to ERA. It’s a bit disjointed, because it’s based upon sample data.

But what you can see is that FIP doesn’t stretch as far as ERA – while ERA on the graph goes from 1.00 to 9.50, FIP runs from about 2.71 to 6.92. (The slope of the line is also rather different.)

So, let’s take an example, from Cyril Morong’s recent blog post about the Dodgers:

ESPN shows that the Dodgers DIPS% is 107, meaning that their pitchers would have an ERA that is 7% higher than it actually is if they allowed a league average of hits on balls in play (they are , of course, better than average). With their actual ERA being 3.61, then their DIPS ERA is 3.86. So here their fielders save .25 runs per game (that is, if the pitchers have nothing to do with batting average on balls in play). The Dodgers have played 115 games, so this is an additional 28.75 runs scored. Adding the 10 in from fewer unearned runs gives us 38.75 runs. Since it usually takes about 10 runs to win one game, a rough estimate is that the Dodgers have won close to 4 games this year with their fielding.

Except.

For an ERA of 3.5, we would expect a FIP of about 3.92, based upon the graph above. If we smooth out that line a bit with a linear regression, we can estimate that a 3.61 ERA should result in a 3.96 FIP. (FIP and DIPS ERA aren’t precisely the same thing, but they are both defense-independent component ERAs based upon linear models of run scoring, so I don’t fee too bad in conflating the two.)

So the effect Morong is seeing here is almost entirely a function of the linearity of FIP, not the Dodgers defense at all.

This doesn’t mean that FIP is useless, of course – it should do a good job of putting pitchers in the right ordinal ranking – the best pitchers will generally have the lowest FIPs and the worst will have the highest, at least within the limits of sample size. But what it will do is distort the distance between the best and worst pitchers.

And that’s why you can’t just subtract FIP from ERA. (Or, again – you can, but you shouldn’t.)

UPDATE: Someone asked about tRA. Well, I have that data, along with xFIP. Excuse me if I’m getting a bit too wild with the Photoshop effects; I promise in a few days I’ll stop feeling like a kid in a candy store and learn some restraint.

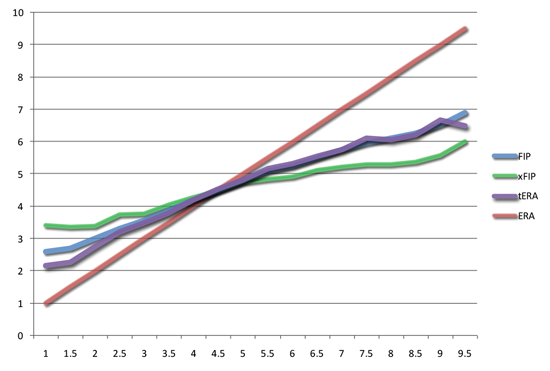
xFIP has an even smaller spread, which should surprise nobody – it normalizes differences between pitchers’ home run rates. This has the benefit of being more predictive of future ERA, one should note.

tRA and FIP are nearly identical in this regard, which again shouldn’t surprise anyone.