A Decision Tree Approach to Pitch Prediction

In some situations, pitchers like Derek Holland can be predictable (via Robert Hensley).
When John Axford burst onto the scene in late 2009, he quickly became one of the game’s most valuable relievers. The righty struck out well over a batter per inning pitched in his first full season, though few made noise when he replaced one of the great closers of all-time in Trevor Hoffman.
In 2012, Axford transitioned from a top-flight closer to a replaceable reliever. The strikeouts were there, but he lost his ability to keep the ball in the yard. He’d be the first one to tell you a few additional home runs can really put a dent in a reliever’s ERA—his doubled from 2011 to 2012 and didn’t budge much for most of 2013. Milwaukee brass, fed up with Axford’s ineffectiveness, decided to deal the righty last August to the St. Louis Cardinals. One “little adjustment” later, and Axford quickly reclaimed the title of dominant reliever.
The righty credits his late-season resurgence to the St. Louis Cardinals coaching staff. Why? Axford had been tipping his pitches. His stuff hadn’t changed much in two years—his fastball was still electric, and he still threw two solid breaking balls—but had become predictable.
From time to time, we’ll hear about about similar examples of pitchers who prematurely expose the pitches they intend to throw. In the case of Zach Wheeler, it was the placement of his glove as he came set on the mound. For Ivan Nova, it was the same issue. I’ve even heard of coaches who are able to sit in the dugout, watch pitchers palm the ball in their gloves, and identify pitch grips by looking at flexed forearm muscles.
Pitchers, like all human beings, are creatures of habit. The act of throwing a pitch is like a mini-routine that gets repeated many times over, and it goes without saying that many are prone to develop tendencies in how they hold the ball, how they stand on the mound, and how they begin their deliveries.
When these quirks are obvious, pitchers can quickly make adjustments. Ryan Dempster waggles his glove when he starts his delivery to avoid tipping pitches, and others simply stop doing whatever it was that made them predictable. It doesn’t really matter how a pitcher solves this problem as long as his solution doesn’t give away any information to hitters.
At the major league level, pitching is all about deception. No matter how fast your fastball may be, or how much your breaking ball may break, the world’s best hitters will beat you if you become predictable. The fact that coaches and players go to such great lengths to keep signals secret and to steal signs from the opposition implies that pitch selection information is very valuable, that there is an edge to be gained in knowing what type of pitch will come next.
The Other Type of Pitch Tipping
Other pitch selection tendencies can’t be picked up by the naked eye and are specific to certain game situations. These patterns can be found in almost every different split you can think of. Pitchers will throw certain pitches more often in certain base/out states, in certain counts, and against certain types of hitters. For example, Zack Greinke loves to throw his slider to righties in two-strike counts—and he’s actually more likely to throw a two-strike slider after having just thrown a slider to a right-handed hitter.
If Joe Buck were to write a how-to baseball book, I’d imagine that the chapter on pitching would start with the following declaration: “Son, you gotta mix things up.” If you were to guess what a pitcher might throw after throwing an off-speed pitch, you might guess anything other than that same pitch. Fastballs should be paired with off-speed pitches to keep a hitter off balance, and vice-versa.
In reality, a lot of pitchers are like Greinke. Josh Weinstock noted in 2011 that major league pitchers are more likely to double up on identical off-speed pitches than to follow an off-speed pitch with a fastball or any other pitch. Pitchers can develop tendencies even when they think they’re becoming unpredictable.
Axford may have been tipping his pitches in 2012 and 2013, but he also wasn’t helping himself out in terms of varying his pitch selection. He hardly ever throws off-speed pitches when behind in the count, allowing hitters to tee off if he misses the strike zone once or twice at the beginning of an at-bat. The righty gave up ten home runs in 2013, and half of those home runs came after Axford fell behind and threw a fastball.
In 2013, Axford was giving two types of signals to hitters: a physical one, which was picked up by the St. Louis coaching staff, and a contextual one, which could have been picked up by anyone with a laptop and access to the internet.
What We Know, and What We’d Like to Know
I’ve spent the last 800 words or so trying to demonstrate that there is value in knowing–before he starts his delivery–what pitch a pitcher might choose to throw. I don’t claim to have any ability to spot the physical quirks that pitchers develop, and I’m not saying that it isn’t worth trying. We should probably leave this job to the coaches who are paid to do it, though.
I will say that I think we can do a little bit better than we currently are at spotting the other type of pitch tipping. The examples I’ve mentioned suggest that the patterns are there, and that if we look hard enough, I think we’ll find them.
We also have a ton of information that gives us the appropriate context to identify the patterns we’re looking for. The PITCHf/x database contains records for pitch selection, situational information, events preceding a pitch, and pitch outcomes. We can’t really ask for much more than that.
All of this information initially can seem overwhelming. Using it to identify patterns by hand would be time-consuming, and we would end up missing things.
Sometimes the patterns we see are obvious, as was the case with Greinke. But what if a pitcher is extremely predictable in a situation we aren’t prone to notice? How often do you think Greinke throws fastballs in two-strike counts when he’s just thrown a breaking ball and there’s a runner on third?
Instead of doing things by hand, we can use a model to do our pattern recognizing for us. This model should be flexible, allowing us to throw in many different bits of information, and it would use the most important factors we provide it with to make predictions. Once we have this model in place, we’ll show it a bunch of data specific to one pitcher. The model will arrange the data in the way that best predicts the next pitch to be thrown.
After asking around*, I decided to work with a decision tree. Decision trees are great at taking a bunch of data, picking up on trends, and displaying the data in a way that allows its viewer to follow these trends.
One clear benefit to a decision tree, as opposed to other machine learning techniques, is that its mechanics are pretty easy to understand. The data start at the top the tree and get filtered through the tree’s branches. At each level, the tree sorts the data through various yes/no questions as it refines its prediction. The most important questions are asked at the top of the tree, and the questions asked toward the bottom refine the tree’s initial guesses.
A quick example: Let’s say the first branch of Greinke’s tree is the handedness of the hitter he’s facing. If the hitter is a righty, Greinke’s overall pitch distribution changes a bit. He doesn’t throw his change-up much (about 4.5 percent of the time, vs. 12 percent overall**), and he throws his slider more often. Against lefties, the opposite is true. After filtering the data through this first branch, our guess improves as we move from his overall distribution to his handedness-specific distribution.
Another advantage to the decision tree is that it doesn’t allow useless information to skew our results. For instance, if I included jersey color as a variable, the model’s suggestions wouldn’t change, and the important patterns still would be doing the predicting.
If the model was reliable, you could put it to use right away. A big league coach, with a single sheet of paper in his hand, could follow the game and signal in pitch guesses if the situation calls for it. Pretty cool, right?
Disclaimers, etc.
The model works best when it is provided with a lot of pitch data. That’s why I immediately eliminated relievers, and why I chose pitchers with at least a few years of full seasons in the big leagues. I used two years of data for each of these pitchers (2012 and 2013), and we have to assume that over this time frame, pitch selection trends didn’t change. Again, I don’t think that this is an issue for the pitchers I chose.
It is also extremely important that this data be classified correctly already and that the pitch types PITCHf/x displays are accurate. The distinction between fastball types doesn’t matter much for this type of analysis, so I re-classified all types as one generic fastball. For the pitchers I chose, I think PITCHf/x does a pretty good job in assigning correct pitch types.
Identifying Possible Signals
Here, I’ll outline briefly what types of data I used to grow the trees. In thinking about what information might be used to identify pitch selection patterns, I began to realize that I was grouping variables into three broad categories:
1) contextual information, or the “game state”;
2) historical information, which can be thought of as a pitcher’s short-term memory;
3) information on the hitter.
Contextual information is probably the most obvious indicator of pitch selection, and we see it referenced often. What does a pitcher like to throw with runners on base? When he’s ahead in the count? Behind in the count?
Pitchers have good and bad reasons for throwing certain pitches in certain situations, but we know that they’re at least pretty consistent about these decisions (most of the time). Below, I’ll list the contextual variables used in each tree. In parenthesis, I’ll note the short-hand name that the model recognizes it by.
- Pitch count (pc) — how many pitches has the pitcher thrown so far today?
- Runners on base (on_1b, on_2b, on_3b) (0=base empty, 1=base occupied)
- Number of outs (outs)
- Count (count)
Recent game events also likely influence pitch selection. If a pitcher has just thrown a slider, we want to know how likely it is that he’ll throw another (once we’ve controlled for context and the hitter he’s facing). This kind of pattern might be more common, but it also might be possible that a pitcher likes to throw a particular pitch after giving up a home run, or after striking out a hitter, etc. Here are my historical variables:
From previous pitch:
- Pitch type (prev_type1)
- Description of the pitch result (e.g. walk, strike, ball, double, foul tip, etc.) (prev_des1)
From two pitches ago:
- Pitch type (prev_type2)
- Description of the pitch result (prev_des2)
From three pitches ago:
- Pitch type (prev_type3)
From four pitches ago:
- Pitch type (prev_type4)
All of this stuff is great, but some might say that historical and contextual information doesn’t mean anything if we ignore the pitcher-hitter matchup. I agree, and I think that the strengths and weaknesses of hitters should be included in the model.
However, the inclusion of data on the hitter a pitcher is facing is tricky. We can’t use season aggregates (unless they come from previous seasons) because season-length statistics evaluate performance in games that have occurred after the date we’re looking at. In other words, we can’t use information from the future to predict the future. On the other hand, a hitter’s value in the previous season may not be a great predictor, either.
The measure I came up with is as close current as I could get. FanGraphs’ database contains game logs for each hitter, and attached to each game exists a total “pitch type linear weight” value, which sums up a hitter’s offensive contribution. FanGraphs catalogues each pitch thrown to a hitter and tags it with a weight, and these values are summed over the course of a game. Positive values represent good outcomes for hitters (balls, walks, hits), and negative values represent bad outcomes for hitters (strikes, outs, etc.). The method was developed by Dave Allen, Josh Kalk and John Walsh.
For the first two months of each season I examined, I averaged a hitter’s per-game run values of the previous season. Then, for the rest of the season, I used a running average of a hitter’s current season per-game values. So, for a game on May 20, 2013, a hitter’s 2012 average per-game run value would be included. For a game on June 20, 2013, individual game performances from Opening Day of 2013 to June 19, 2013 would be averaged.
This measure works pretty well in quantifying the strength of a hitter on a single day—but I also looked at a hitter’s spot in the lineup (thinking pitchers might be ignorant to specific match-ups and pitch similarly to all leadoff hitters, etc.).
Pitchers may also base pitch selection tendencies on the level of patience of the hitter he’s facing. I used the same date-averaging technique that I used on per-game run values to create a “pitches seen per game” variable, which helped identify a few interesting pitcher-specific patterns.
To recap, here are the hitter variables included in the model and the labels attached to them:
- Hitting from left (L) or right (R) side of the plate (stand)
- Average per-game run value (avg_BRAA)
- Average pitches seen per game (avg_pitches_seen)
- Batting order position (1-9) (BatOrder)
- For National League data: Position (Pitcher(P) or Fielder (F))
Now that I’ve made the meaning of each model component clear, we’re ready to spot patterns in actual pitch-selection decision trees. When building each tree, I had to make decisions on how far the tree should go in terms of filtering the data.
We gain the ability to generalize the results a little bit better when the model has a threshold (say, ten pitches) after which it wouldn’t determine a particular subset worthy of a filter. The tradeoff, though, is that a broader tree misses out on interesting bits of information that may or may not be predictive.
For example, you’ll see in Justin Verlander’s tree that “home run” is not included in any of the “prev_des” filters. This is because the model decided that we didn’t have enough data from pitches hit for home runs off Verlander to make a pitch prediction.
When I ran the model without a minimum cut of 15 pitches, however, I found that Verlander followed up home runs hit off fastballs with another fastball 10 of 14 times and followed up home runs hit off an off-speed pitch with change-ups eight of nine times. Do what you want with that bit, but it will fit in pretty nicely with our profile of Verlander being a guy who likes to double up on pitch types.
I’ll start with a relatively simple tree I created for Derek Holland. Holland is mainly a fastball/slider guy, but he does throw in a handful of curveballs and change-ups per start. As we get our feet wet, I’ll use a 15-pitch minimum for making cuts in order to create a (relatively) simple tree.
Start on the left side, and work your way over. The red cells contain predictions, and the numbers in parenthesis list the number of test cases predicted correctly and incorrectly.
Derek Holland — Pitch Selection Decision Tree (Simple)
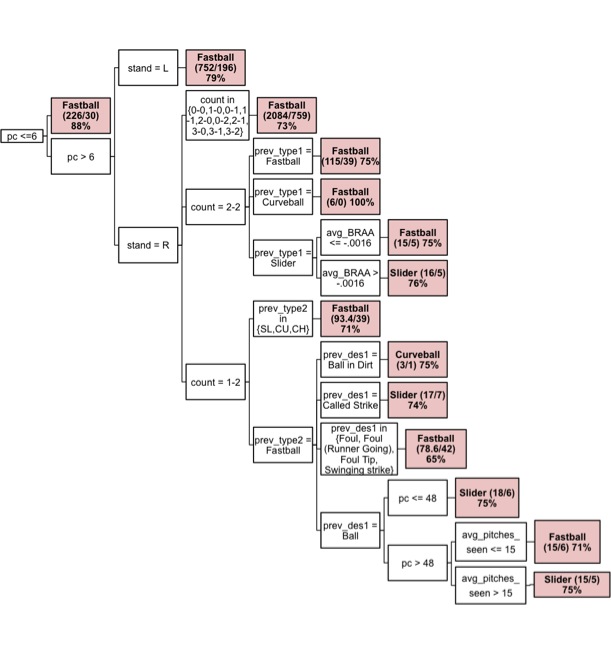
(Note: why do we have fractions of pitches in our trees? If the model is missing a value for an observation, it sends half of an observation down each side of the tree.)
Let’s take a look at the first two cuts the tree makes. If Holland has thrown six or fewer pitches in this start, the model stops asking questions and predicts a fastball will be thrown next. If Holland’s next start is anything like what we’ve seen from him in 2012 and 2013, this would be the correct call about 85 percent of the time.
If Holland’s pitch count is higher than six, the model then splits the data based on hitter handedness. If Holland is facing a left-handed hitter, he throws fastballs about 80 percent of the time. If he’s facing a righty, we continue down the tree.
Even in a simple tree, things can get complicated pretty quickly. Say Holland has just missed the zone with a slider on a 1-2 count to run the count to 2-2. If Holland is facing a relatively bad hitter (one with an average per-game run value below -.001), he’s likely to throw a fastball next. Against better hitters, however, he likes to throw another slider in these situations.
Holland’s generalized model provides a few interesting situational recommendations, but it does not do a great job predicting across all situations. To do that, we’ll have to modify our restrictions a little bit.
In this next example, I created a tree for Verlander that makes use of a branching sample size minimum of 10 pitches. Verlander throws his secondary pitches more often than Holland, so his tree should be a little bit more interesting. The full diagram is too large to fit on this page, so I broke things out after the tree’s first cut (hitter handedness). Again, red cells end in predictions.
Justin Verlander — Pitch Selection Decision Tree

 Verlander is a pitcher who clearly plays on hitter aggression/passivity. In this model, my “pitches seen per game” variable is used to filter more data than any other piece of information. (That is, after we sort out the count and batter handedness, which tends to happen first for every pitcher I looked at.)
Verlander is a pitcher who clearly plays on hitter aggression/passivity. In this model, my “pitches seen per game” variable is used to filter more data than any other piece of information. (That is, after we sort out the count and batter handedness, which tends to happen first for every pitcher I looked at.)
When Verlander gets right-handed hitters into an 0-2 count, he’s likely to throw a slider to aggressive hitters, but against patient right-handed hitters, his put-away pitch selection is more of a toss-up.
Verlander also likes to throw a ton of change-ups to patient left-handed hitters. When the bases are empty, he’ll throw it when he’s ahead and when he’s behind to this type of a hitter. If you’re patient enough, he doesn’t mind throwing two in a row.
One more interesting thing about Verlander’s tree: the importance of runners on base. With runners on first, second, or third, he starts both left- and right-handed hitters with fastballs around 75 percent of the time. We don’t have many other pitchers to compare to in this respect yet, but that’s almost 20 percentage points higher than his baseline fastball usage. I think this bit is exactly the kind of thing that we’re looking for–a habit for Verlander, but maybe something he isn’t aware of.
Now that we have a slightly more complex model to look at, we should evaluate its performance in doing what I originally set out to do, predict future pitch types.
When I created the tree you see above, I used 80 percent of Verlander’s 2012-2013 for training and building the tree. I then set aside 20 percent of the data to be used for testing the model. This data will look like data from the future, in that the model hasn’t seen it before.
The official model “error rate” in guessing pitch selection for this “new” data is around 50 percent. That sounds terrible (and it kind of is), but it doesn’t really represent an accurate comparison to the alternative, which would involve picking pitches randomly from his overall distribution.
For example, we know Verlander throws fastballs about 60 percent of the time. If we pick 60 percent of all pitches he’s thrown at random, we won’t get all fastballs. We’ll get some change-ups, some sliders, and some curveballs. There are four types to choose among, so random selection actually performs a little bit worse than we’d think. How does this model compare?
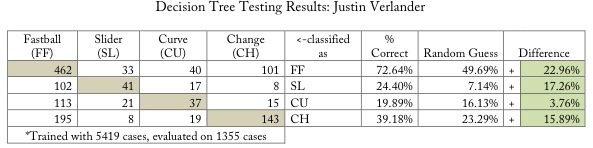
All in all, this model performs significantly better than picking pitches at random from Verlander’s normal distribution. Is it better than we are? That’s a tougher question to answer. Next time you’re watching your favorite starter pitch, try guessing the next pitch he’ll throw. After trying that with a Verlander start, I began to appreciate the model’s 39-percent accuracy in guessing change-ups.
That last attempt went better then I’d hoped, but let’s try one more time. With Clayton Kershaw, I took things one step further. I played around with a few different models, but I settled on one that used no minimum branching sample size. If Kershaw has thrown a slider three out of three times in some very specific situation over the last two years, this model will include that as a factor.
The result was a tree with 537 branches—which is obviously too large to include in this article. I won’t go into the details of the tree here, but an analysis of that thing could be an entire article in and of itself.
The reason I bring up this really complex tree, though, is that I thought it might do a better job predicting pitch types than Verlander’s sort-of-complicated tree. I also assumed that the complex tree would be better at identifying a pitcher’s least-used off-speed pitches, because sample size issues often force off-speed guesses to be omitted from simpler trees.
So how does it do at predicting Kershaw?
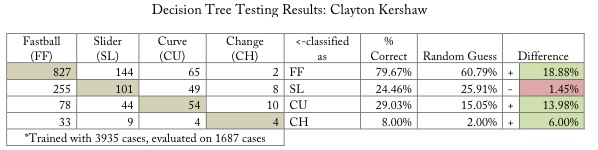
*Kershaw’s data was tested and trained on a 70/30 split, because he’s thrown fewer pitches than Verlander.
I should note that, in comparison to Verlander, Kershaw doesn’t give us as much data to work with. (Actually, when we compare to Verlander, no other pitcher does.) Kershaw also doesn’t throw his off-speed pitches as often as Verlander does, which makes it even tougher to predict these pitches. Kershaw’s model is worse at predicting sliders than random guessing would be, and it is significantly better at predicting fastballs and pitches that Kershaw throws really infrequently.
The sweet spot, in terms of model restrictions, likely should be specific to each pitcher. For Kershaw, it might have been a better idea to exchange one correctly-predicted change-up for better fastball and slider accuracy.
Complex trees also do a great job capturing a pitcher’s “attribute usage,” a measure of how often each variable is considered. I mentioned that, for Verlander, hitter patience is a critical predictor. And for Kershaw?
Attribute usage (Clayton Kershaw):
100% — count
76% — position (Pitcher/Fielder)
53% — prev_type1
44% — stand (hitter) (L or R)
43% — on_3b
39% — prev_des1
37% — pitch count
34% — prev_des2
28% — on_2b
18% — prev_type2
17% — on_1b
16% — outs
15% — prev_type3
13% — BatOrder (1-9) (hitter)
10% — per-game run value (hitter)
8% — average pitches seen per game (hitter)
6% — prev_type4
Not so much. Contextual information seems to be what this model considers to be most often predictive of pitch type. Information on the hitter (other than handedness) is also considered, but not in as many cases. This kind of a chart can be useful in telling hitters what to look for when they’re about to face Verlander. It also allows someone to pick out a tree’s most significant suggestions.
Wrapping Things Up
There’s so much more that can be done to pull interesting tendencies from pitch-selection data. We can run multiple models to validate what we’re seeing, adjust our prediction confidence level, and even split one complicated tree into many simpler sub-trees (I’ll get back to you on that one).
I also can work on the information that is fed to the tree: can we come up with a better measure of hitter value? Another contextual variable? Can we include more data without picking up outdated trends?
Can we take it a step further and predict pitch location? Can we use location data to make predictions? No, that just wouldn’t be fair.
I learn something new every time I take another look at one of these trees. I intend to keep creating them for starting pitchers, so feel free to suggest someone you think might display an interesting pattern.
References & Resources
- Many thanks to Dr. Raghuram Ramanujan for his help throughout the model selection process.
- Thanks to Brooks Baseball for their awesome PITCHf/x player cards.

I do some of these in my job (not baseball), a few things to keep in mind-
If a pitcher is changing his patterns in the data you look at, due to interntional strategy or injury, the tree will do a terrible job.
You would hope that any final tree would do better than “throws most common pitch” when guessing. A baseline for the usefulness of the model is whether it can do better than that, not a “pick random pitch from distribution” baseline. I can get Verlander right 60% of the time by guessing fastball every time. If the tree can’t do better, then it doesn’t help. Since the training data did much better than the testing data, it’s likely you have overfit the training data.
Good article, thanks for writing it. I would agree with AWEB, that its unfortunate the testing data didn’t measure up to the training data. Despite that, I still find it interesting, and it feels like you could be onto something.
I especially like the attribute usage, as it seems to give some insight into the thought process of the pitcher, which seems useful. I wonder if there are any major differences among pitchers… or if there are certain “types” of pitcher categories here.
Wonder if it might be better with a binary: “fastball” vs “off-speed”, rather than breaking down each type of breaking ball.
Would like to see trees run for Cliff Lee and Cole Hamels of the Phils. Cole seems very intense and thoughtful about his craft, while Cliff seems very happy-go-lucky about his. Two lefties, good pitchers, same team/time, good amounts of data… might make an interesting comp.
aweb-
That’s a great point. I think the point of these trees is to find a few specific situations in which a hitter is likely to see one specific pitch. The tree also allows us to be much more confident about some fastball guesses (example: Verlander’s first pitch with runners on base).
On the whole, I figured that no pitcher is predictable on every pitch. I would argue, though, that random guessing is closer to reality. I think we tend to overestimate the use of off-speed pitches, so it would be tough to tell a hitter to “guess fastball most or all of the time.”
Dave-
“Fastball” vs. “off-speed” could definitely work. Another option would be to omit infrequent off-speed pitches? I’d be reluctant to do that kind of thing the first time through, just because we’d lose out on guesses that are potentially really valuable. Finding a change-up in Clayton Kershaw’s pitch distribution is like finding a needle in a haystack, but some pitchers may look to throw their fourth pitch in specific situations.
Cliff and Cole would be a great pair to compare!
Really interesting stuff. I wonder how many of these tendencies are used by hitters/coaches for game prep.
On another note, one possible way to improve the error rate of the model would be to default to fastball unless the alternative had a large enough sample and high enough percentage of non-fastball use. While it looks like you already did that to a certain degree, raising the minimum requirements for a non-fastball guess could improve the accuracy (even if it means the model predicts fastballs 80% of the time even when we know the pitcher only throws fastballs 60% of the time).
The official model “error rate” in guessing pitch selection for this “new” data is around 50 percent.
Interesting article Noah. Times through the order might make a better predictor than pitch count. It may be beneficial to do separate trees for different catchers for each pitcher or at least test whether different catchers lead to different pitch type distributions overall for a pitcher. Pitch distributions used by a pitcher in prior matchups with a specific batter or a pitcher’s prior success with a batter on certain pitches might also yield useful results.
I am also interested in how much the catcher effects pitch selection. The 2013 Tigers would be good to look at since only a small number of starts were made by a sixth pitcher.
It seems like you are overfitting the data (that is, adding in too many predictor variables), and there isn’t enough signal there to actually predict pitches with any accuracy. As people pointed out above (and tango did on his website), the best and most accurate strategy is to always predict fastball.
With that said, it seems like a really promising approach, and I hope that you can develop it in the future to the point where pitch selection is actually predictable. (The catch-22 is that if you do that, we probably won’t hear about it because a team will have hired you). If you can stomach it, a more complex machine learning algorithm may be very useful in this.
Very interesting article. What software are you using to perform this analysis? I’ve experimented a bit with WEKA, which can apply similar algorithms. The software you’re using seems to have more detailed information on the model ouputs (like your attribute usage stats), so I’d love to check it out.
Really love this line of questioning, Noah. In fact I spent a while in Nov/Dec I think looking at exactly the same question, and had even looked at Kershaw as my test subject. I was trying a neural net based on many of the same parameters that you used. I also used the time through the order (as Peter Jensen mentioned above) as an input variable.
In the end, I never really got to a point where I felt it was useful. I agree that this would be the one question that I think hitters could really use the answer to the most when going up to the plate – what is most likely coming? The thing that I found (in as far as I got with my approach) is basically what Tango said – it was pretty hard overall to do better than just predict fastball all the time for me. Which is sad…but doesn’t mean it can’t be done. I did at least learn a bunch about what Kershaw will/will not through in certain situations! (It’s amazing that I had also used 2012-2013 data….he threw only one curveball during that time when behind in the count)
Nice effort here and I hope you keep going…if not with this than the other questions in your head, as we seem to be probing at the same topics lately!
Thanks, Jon. I agree, and I think it can be evaluated on two levels. Right now, it can’t be used to predict every single pitch. I’m not so confident that it ever could be, but who knows!
As you pointed out, I think it can (at this point) be effective in coming up with situational recommendations. I went with the decision tree over a neural network with the hope of catching some of the patterns I talked about in the article, but also for the ease of presentation (Matt- I would hope something like this could be used for game prep!). I wanted to avoid creating a “black box” that shoots out predictions.
Jim- I used C5.0 (which is free) to make the trees. It shoots out a pretty extensive overview of what you see in the article, plus a few other things.
Peter and Ben- the catcher stuff is where I might be heading—Yadier Molina came to mind right after I wrote this. One issue (that I could use help with) is coming up with pitchers who allow Molina to call the game, and who rarely shake him off.
Interesting article! Thought I would share a story about Babe Ruth. He was apparently tipping his pitches and his coaches checked him over and over and couldn’t figure it out for a while. Finally, somebody noticed that he was tipping his pitches with his tongue, sticking out of the corner of his mouth, while pitching!
Also, there is a story, not sure if true, but reportedly Bonds was sitting in a box behind home plate and called over 90% of the pitches thrown. But that jibes with a story that Duane Kuiper told his radio show of how Bonds told him and Krukow (Giants announcing team) on the plane the first 12 pitches that Maddux would be throwing him in an upcoming series, and darn if he didn’t nail most of them.
I wonder if park effect, or knowledge of park factors by a pitcher/catcher plays a demonstrable part in pitch selection? Secondly, does having differing catchers from situation to situation effect the outcomes/choices? Great study.
I’m certainly no mathematician or statistician (and I’m also at work and on my phone) but one potential flaw with this approach I see would be in which order should the model make its “cuts”. For example the second cut it makes is by hitter handedness but what if other factors are present in a particular AB that may negate (or even hurt) any value from that particular cut? Like in the Verlander example you mention. “”One more interesting thing about Verlander’s tree: the importance of runners on base. With runners on first, second, or third, he starts both left- and right-handed hitters with fastballs around 75 percent of the time.”” , would it make more sense for the model to take into account this data BEFORE dissecting the current AB further? In that scenario the model already has narrowed it to a 75% chance he will throw a FB. I like your model a lot and I feel finding some way to weight the data available and then have the model make it’s cuts you could increase your predictive success rate above 39%.
This is a very interesting and well written article. It shows that there is a lot of value in PITCHf/x data. I have a few suggestions for refining your research.
1. I second Matt’s suggestion: “On another note, one possible way to improve the error rate of the model would be to default to fastball unless the alternative had a large enough sample and high enough percentage of non-fastball use. While it looks like you already did that to a certain degree, raising the minimum requirements for a non-fastball guess could improve the accuracy (even if it means the model predicts fastballs 80% of the time even when we know the pitcher only throws fastballs 60% of the time).” Such a threshold will also help with the overfitting problems.
2. You should also consider using a random forests algorithm. This is an ensemble of decision trees. There are free packages for this algorithm available in various computer languages. Also, Wise.io (http://www.wise.io/) has a web based implementation (note that it is not free).
3. I suspect that your modelling of batters faced is causing problems. You may want to use something simpler such as batter’s place in the order (top third, middle third, bottom third), a category of pinch hitters, and discard pitchers from the data.
4. For situations in which your model does not meet the threshold mentioned in #1, you should consider using another random forests algorithm with this data and shallow trees and less refined attributes. The goal here is to generate predictions that are statistically relevant yet better than using pitch % data.
Great article and the decision tree rocks. My approach as a hitter was to pick out one or two of the opposing pitchers best pitches and practice hitting those in his favorite locations in preparation for the game. Then knowing he would throw that pitch / location at some point in my at bat I would just look for that pitch and hit it when it came.
The expanded tree for Kershaw with 537 branches sounds like a classic case of overfitting. Ideally what you’d want to do is break the pitcher’s data set into two halves, build and tune your model off the first half, then test it on the second half to see how well it performs. Don’t tune the model using the full corpus of data.
http://en.wikipedia.org/wiki/Overfitting
Guess I should have read the other comments first. D’oh.
Very much enjoyed this read. Excellent job. It made me think of a number of questions, and I can see how this is something that your brain wants to keep digging on. Some of the things I thought about:
1. Outcome – The decision trees are awesome when used to identify a pitchers tendency towards the selection of one pitch over another. Are those tendencies based in previous experience; previous history with the given hitter or on that given night? Could a pitcher be evaluated on his (or the catcher’s) decision-making vs. the “book” call that the given situation? I suppose much of this has to do with the effectiveness of the pitch execution.
2. More Hitter Variables – I loved your inclusion of Pitches Per At Bat. I’m wondering how and if this can be flipped to evaluate hitter selectivity and the effectiveness of their selection (“I was sitting on his fastball.”)
3. Minutiae – The depth of branching options is really fun. Does the pitcher have an injury? Do the not have command of a particular pitch on a given outing which causes them to over rely on another? What about weather?
Again, great job on this. I really have limited understanding of the advanced metrics but this makes me want to spend more time understanding it and most importantly, continue to enjoy watching baseball. Really enjoyed it. Thanks!