Adjusting defense efficiency by the quality of pitching
Fausto Carmona throws a hard sinker on the outside corner, but Ichiro Suzuki turns it into a well-struck ground ball by going the other way, splitting the defenders on the left side of the diamond. We know who should get credit for the single on the Mariners’ side of the box score—there was only one guy with a bat. But who on the Indians will take the blame for the single? Is it Carmona who made the pitch, or the defenders who could not get to the ball fast enough?
Bill James invented Defensive Efficiency, measuring the percentage of balls in play that a defense turns into outs. It became apparent just how useful this would be for evaluation of team defense when Voros McCracken famously concluded that, “There is little if any difference among major-league pitchers in their ability to prevent hits on balls hit in the field of play.” A natural corollary to this thesis says that to measure team defense, one should use Defensive Efficiency rate.
However, since McCracken’s original thesis, the community has determined with certainty that while there is little difference between pitchers, there definitely are some major “little” differences. Following on work by J.C. Bradbury and others, I have shown that a pitcher’s ability to control the number of hits he surrenders on balls in play is well correlated with strikeout rate, walk rate and ground ball rate, the so-called “DIPS” (Defense Independent Pitching Statistics) that are not determined by the defense behind a pitcher. In fact, a pitcher’s BABIP in a given season correlates more with his DIPS the previous season than with his BABIP the previous season. In other words, DIPS predicts BABIP better than BABIP itself does.
As I close in on how to measure a pitcher’s ability to control BABIP without actually using what happened on balls in play, I have realized that I can actually see how much of team defensive efficiency is the fault of hurlers. It turns out that a large portion of defensive efficiency is pitching after all. I have shown the following to be true:
A) Pitchers who strike more hitters out give up fewer hits on balls in play.
B) Pitchers who induce fewer ground balls give up fewer hits on balls in play.
C) Pitchers who walk fewer hitters give up fewer hits on balls in play.
Using this information, I have found that the variance in BABIP among starting pitchers who pitch over 150 innings can be attributed approximately as follows:
A) 12 percent pitching skill
B) 13 percent team defense skill
C) 75 percent luck
Of the fraction that pitchers do control, you can predict about 10.4 of those 12 percent using DIPS. Yes, pitchers do exhibit some control over their BABIP, but in an entirely estimate-able way. I think this passes the smell test, too, because if I try to imagine a pitcher who you expect to limit hits on balls in play, I picture one who fools hitters into whiffing a lot too, or perhaps one who pops a lot of hitters up.
One of the most underrated aspects of SIERA is that it implicitly computes an “Expected BABIP,” by using regression techniques. Since it looks directly at expected ERA, conditional on strikeout rate, ground ball rate, and walk rate, it does not directly compute the effect of a strikeout on ERA; instead, it computes what pitchers’ ERAs will look like given their strikeout rate (and holding everything else constant). Thus, SIERA expects high-strikeout pitchers to have low BABIPs, and makes similar adjustments for ground ball rate and walk rate as well.
As I considered how individual pitchers’ DIPS correlate with expected BABIP recently, I realized that there are considerable differences among whole teams in their strikeout and ground ball rates. The 2010 Giants struck out 21.6 percent of hitters faced; the 2006 Royals struck out only 14.1 percent and unsurprisingly had a team BABIP that was 24 points higher than the 2010 Giants.
Putting this all together, I found that the variance in team defensive efficiency can be attributed roughly as follows:
A) 48 percent team defensive skill
B) 40 percent luck
C) 12 percent pitching skill
With about 4,350 balls in play per team per year, you get rid of most of the luck, so this number shrinks to just 40 percent, and of course, team defense still explains BABIP better than anything else does. However, a very large part (12 percent) of keeping a batted ball from resulting in a hit is pitching. (Put in a mathematically equivalent but different way, there is a .37 correlation between a team’s Expected BABIP based on its pitching peripherals and its actual BABIP.)
To study this more objectively, I redefined “BABIP” to include errors, and ran a regression on all individual pitchers in the majors in 2002-2011 with 80 balls in play or more, weighted by balls in play, and using net ground ball rate ((GB-FB)/PA), strikeout rate, walk rate, all of their squares and interactions, dummy variables for season, and pitcher starter/relief role.
Then I simply applied this to each individual’s pitching statistics, and came up with an expected number of batters reached per ball in play with neutral defense and luck. Then I used that to develop an expected “BABIP” (with errors) for each team.
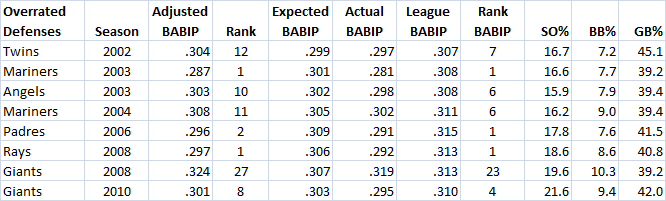
The lowest expected team BABIP (relative to the rest of their league) belonged to the 2002 Twins, with just a .299 expected rate of reaching on balls in play, below the league average of .307. The actual Twins allowed a .297 BABIP, which means that they were good defensively and also good at pitching, resulting in particularly few hits.
The highest expected team BABIP (relative to the rest of the league) belonged to the 2007 Blue Jays, who had a .321 expected BABIP, as compared with a .316 league average that year. The actual 2007 Jays’ BABIP was a very low .297. Their defense was actually fantastic, and their pitching made it harder and cost them the league best BABIP. Relative to their expected BABIP, their 19-point lower actual BABIP was the best in the league, but they finished millimeters behind the Red Sox. However, the Red Sox had pitchers with more strikeouts and lower ground ball rates, and their defense had a much easier battle to make outs.
Overall, there is pretty high year-to-year correlation in a team’s expected BABIP, .47, which is not so shocking since teams generally do not turn over most of their pitching staff in an offseason. This highlights the fact that one cannot look at aggregate numbers over a longer period of time to determine how teams play defense, hoping other factors will wash out; a defense can look bad for several years, when the pitchers should actually shoulder the blame.
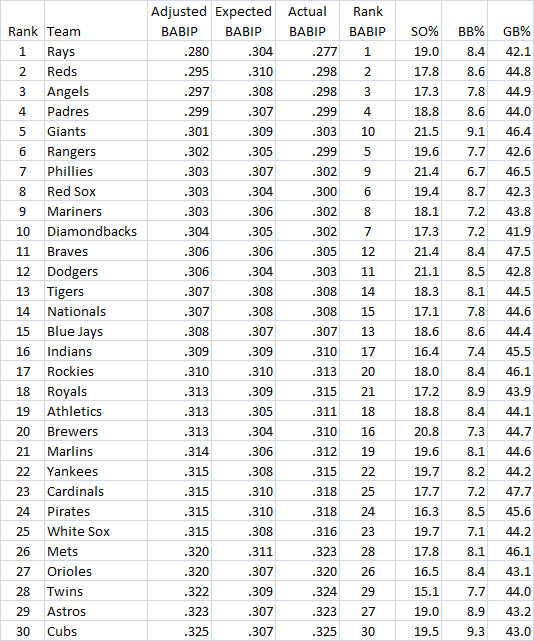
Below I list teams by their 2011 ranking in “adjusted BABIP.” This is done by taking their actual BABIP (again, including errors as hits), and adjusting it for their expected BABIP based on their pitchers relative to the league BABIP. I also include the team’s ranking by actual BABIP surrendered, for comparison.
Of particular note is the Giants, who would have been 10th overall in BABIP, thanks to a somewhat wild pitching staff that was rather groundball prone, but still managed to make a lot of outs. Relative to the high BABIP that would have been expected given their pitching staff, the Giants actually appeared to have the fifth best defense at recording outs per ball in play.
Hurlers like Tim Lincecum, Matt CainJonathan Sanchez simply do not allow hitters to get good wood on the ball, and as a result, the defenders behind them look strong behind them when batters do make contact. On the other hand, the Diamondbacks were ranked above the Giants, at seventh, using BABIP alone, but their high-flyball stuff actually requires an adjustment to bump them down to 10th. (Again, recall that BABIP here includes ROE as hits.)
For all of the rankings for 2002 through 2011, see this Google Doc.
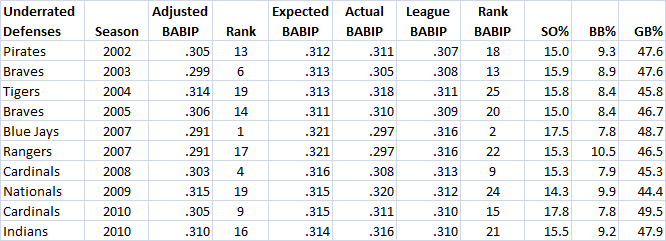
There are a number of interesting examples of teams whose defensive efficiency can be reinterpreted based on their pitching stats. The following table gives my favorite examples of teams re-interpreted using this method, some of which I describe below.
The 2010 Giants were actually on the other end of the spectrum than the 2011 Giants. They had a similar high strikeout rate and walk rate, but their groundball rate was much lower, making their expected number of outs much higher, since fly balls are easier to catch.
This was partly due to Matt Cain’s groundball rate going up from 36.2 to 41.7 percent. It was also due to replacing Barry Zito’s 33 starts with a 36.1 percent groundball rate in 2010, with just nine Barry Zito starts at a 39.8 percent groundball rate in 2011, and 45.6 percent ground balls in Ryan Vogelsong’s 28 starts in 2011. They also got 15 more starts out of Madison Bumgarner, whose groundball rate was 45.1 percent in 2010 and 46.0 percent in 2011, instead of Todd Wellemeyer’s 33.5 percent groundball rate in 11 starts as they received in 2010.
In both seasons, the Giants had fantastic strikeout rates that we know correlate with less hittable pitches, and more catchable balls in play, but the groundball rate was very different in 2010 and 2011.
The 2003 Mariners were an interesting story of run prevention. A large part of their league-leading defensive efficiency was fantastic defense. They had an outfield of Ichiro Suzuki in eight (21.1 UZR), Mike Cameron in center (19.6 UZR), and Randy Winn in left (4.3 UZR), combined with an infield that featured John Olerud at first base (11.0 UZR), Bret Boone at second (10.4 UZR).
But they also had an excellent flyball staff that kept the ball catchable in the first place. Jamie Moyer had 215 innings pitched with only a 38.3 percent groundball rate, Freddy Garcia had a 41 percent groundball rate in 201.1 innings, Gil Meche had a 36.8 percent groundball rate in 186.1 innings, and Ryan Franklin had a 34.3 percent groundball rate in 212 innings. The only starter who was not particularly flyball prone was Joel Pineiro, who had only a 45.4 percent groundball rate himself.
None of these starters were particularly good at missing bats, but their extreme flyball tendencies made up the difference. When combined with their fantastic defense, the 2003 Mariners were fantastic at making outs.
The 2007 Rangers relied on their 46.5 percent groundball rate to keep opponents from scoring, which has the side effect of permitting a lot of singles. On the down side, they struck out only 15.3 percent of hitters faced. As a result, they were 22nd in the league in preventing hits on balls in play.
However, they would have been 17th if they had an average staff in terms of BABIP skill. Pitchers like Kameron Loe, Kevin Millwood and Vicente Padilla contributed to the high groundball numbers without striking enough hitters out to shorten swings and reduce BABIP.
The Nationals trailed the league at striking hitters out in 2009, whiffing only 14.3 percent of hitters. Unsurprisingly, the Nationals were 24th in defensive efficiency in 2009, but they would have been right near the middle at 19th if you adjust for their staff. John Lannan, Craig Stammen and Shairon Martis are hittable in all the ways you would expect—they do not strike hitters out and hitters make better contact with the ball as well.
The Indians took away the dubious crown for worst strikeout staff in the league in 2010 from the Nationals, and they allowed a lot of hits too. Their defensive efficiency was .316, definitely below average, but their pitching numbers suggest that it should have been .310 anyway, reapportioning most of the blame from the defense to the pitchers.
Disentangling credit between pitching and defense appeared to take a great step forward with McCracken’s discovery about pitcher BABIP control (or lack thereof), and this is assuredly one of the most important findings of sabermetrics. However, as analysts collectively step back from the extreme position that a pitcher should never be blamed or credited for his BABIP, we should also reinterpret team defensive rankings as well. A full 12 percent of variance in team defensive efficiency is directly attributable to pitching. As we always knew, there are many factors in play once the ball hits the bat.

I loved the article. Great stuff.
Also, would park factors come into play heavily when making these conclusions?
Great article, Matt; it’s fun to see the pendulum swing back a bit from the casual “No pitcher control over BABIP” references that get made here and there. I had a couple of questions:
1. “it does not directly compute the effect of a strikeout on ERA; instead, it computes what pitchers’ ERAs will look like given their strikeout rate (and holding everything else constant).”
I had to reread that a couple of times to make sure what it was saying, but I think I’ve got it – basically, the coefficient attached to strikeout rate is the effect on ERA associated with strikeout rate, which includes both the direct effect (strikeouts) and indirect effects (things that go along with strikeouts that aren’t already measured by walk rates, ground ball rates, etc.). This is a consistent feature of regressions, right? You’re measuring the correlations which can’t really differentiate direct from indirect effects (or causes from effects, for that matter) unless all of the plausible indirect effects were accounted for by other variables.
2. An unrelated, more general saber-question: Curious as to what you think about the term “luck.” I know it irks some people, and it seems like at least occasionally it means “random variance *plus* unknown and/or unquantifiable effects” and not just “random variance.” How do you explain the concept to the casual fan?
@Ryan:
Yes, park effects do play a role here. James Click did some great work in creating PADE (Park-Adjusted Defensive Efficiency). That re-ordered teams much like the pitcher-adjusted defensive efficiency that I did here. Ideally, you could do both.
@Nyet:
Yes, that’s what I meant. Sorry. It picks up direct + indirect effects. FIP actually measures the direct effect of a strikeout per IP, so you can basically figure out the indirect effect with a little calculus. If you take the derivative of a strikeout with respect to SIERA, and plug in league average values for strikeout, walk, and groundball rates, and then adjust for an approximation of IP/PA, you get a FIP-scale coefficient on Ks for SIERA of 2.9, as oppose to 2.0 FIP, so it’s like an added 45% of indirect effects on top of direct.
For league average pitching all around, the FIP-ified SIERA for an all-around average pitcher would be:
SO: 2.0 FIP, 2.9 SIERA
BB: 3.0 FIP, 2.9 SIERA
Flyball: 1.3 FIP, 0.7 SIERA
(Flyball is really 13 as HR, but I’m re-calibrating for 10% HR/FB like xFIP).
As for your second question, it’s a tricky one. Casual fans have very different backgrounds, and so the concept of luck should be explained differently depending on who you’re talking to. If you want to talk to a mathematically competent casual fan, you can talk about binomial variance, and just say this pitcher will allow hits on 30% of balls in play, but that means that in X balls in play, the spread of BABIP will be Y, and will affect ERA by Z. If you want to talk to a less mathematically inclined casual fan, you can just talk about how a certain number of hard hit balls turn into outs and a certain number of soft hit balls turn into outs, and for this pitcher, those rates were abnormal, but that isn’t usually sustainable. Stuff like that. It really depends who you’re talking to, to be honest.
The community has shown with certainty that there is little difference between pitchers? I would say that my study of HITf/x data indicated exactly the opposite.
And similarly for team defensive efficiency, a large portion of it is due to how hard the team’s pitchers allow the ball to be hit.
Single-year BABIP is a crude measure of pitcher skill, and it’s leading you to conclusions about the game of baseball that are very wrong.
Very interesting read, thanks
You wrote:
“Pitchers who induce fewer ground balls give up fewer hits on balls in play.”
I can’t access the BP article you linked to, but this sounds like a surprisingly counter-intuitive conclusion. Did you mean to say that pitchers who induce MORE ground balls give up fewer hits on balls in play? Or is there some correlation between DIPS and weak flyball contact like IFFB?
“Pitchers who induce fewer ground balls give up fewer hits on balls in play.”
BABIP is higher on ground balls than on fly balls, so intuitively it makes sense.
Mike:
I’m not coming to any wrong conclusions. I don’t know what you think I’m doing with single season BABIP, but it’s not leading myself to wrong conclusions.
There IS little difference relative to the difference between pitchers in strikeout rate, which is why it takes more than a season to stabilize.
What your study showed was that how hard balls are hit is persistent, and that it is correlated with BABIP. It didn’t widen the spread of pitcher BABIP skill levels in the MLB, which is and always has been minimal compared to the spread in strikeout rates.
I find your comment about “leading you to conclusions about the game of baseball that are very wrong” to be fantastically indicative that you haven’t really read and understood this or anything else I’ve written on the topic of pitcher BABIP. If you did, you could certainly understand your own findings better, and you’d know they aren’t contradictory.
The reason that single season BABIP is a crude indicator of pitcher skill is sample size. The variance in an individual’s BABIP skill level due to randomness is going to be about [.21/sqrt(number of batted balls)]. Knowing this, we can actually pin down that about 75% of single season BABIP variance is due to luck for pitchers with >=150 IP. The rest of it comes down to know the other 25%. We know that regressing team BABIP by the same process would yield another 13% of the variance in BABIP, which means that there is 12% for pitching.
Using single season BABIP to understand that 12% will due a pretty poor job. However, using peripherals and running a regression as I have will eliminate a lot of that noise. In fact, you can explain about 10.4% of that 12% by knowing peripherals. What your study likely did is duplicated some of the effort in understanding the first 10.4% (hard hit balls or correlated with peripherals; check your data, I’m sure it’s true) and supplemented a good portion of the remaining 1.6%.
In other words, nothing you found negates anything I’ve found at all. You’ve come up with a way to use propietary data effectively. Unless you have that available, using peripherals does a pretty good job. I can’t even imagine what it is that you disagree with here, or what you think I don’t understand.
Bojan:
You’re correct, it was a typo. Sorry. GB% is positively correlated with BABIP, but it does go down for very high GB%. The highest BABIPs would be around 50% GB rate, all else equal.
I’m not disputing your statistics. I’m disputing your conclusions about the game of baseball.
“What your study showed was that how hard balls are hit is persistent, and that it is correlated with BABIP. It didn’t widen the spread of pitcher BABIP skill levels in the MLB, which is and always has been minimal compared to the spread in strikeout rates.”
Right. But I did show that BABIP is a poor way to measure pitcher skill. We sorta knew that already, but some people had taken the BABIP findings to mean that pitcher skill was also minimal. I established that that conclusion from the evidence was wrong.
You are correct that strikeout rate picks up some of the hard-hit ball skill that pitchers have. However, it does not pick up nearly all of it.
Moreover, batted ball categories are pretty good at picking up vertical launch angle effects, but they are lousy at picking up how hard the ball is it.
So your regressions are still missing some pretty important data.
Yes, the ways we have found to measure that data so far are proprietary. That doesn’t mean that we shouldn’t learn about the reality of baseball from that data and let that effect how we frame questions, though. I would certainly wonder why BABIP doesn’t better reflect how hard the ball is hit.
I found that almost half of team BABIP was due to how hard the ball was hit. So when you say it’s 12 percent pitching skill, that’s what I’m disputing. You could say that you can only detect that 12 percent of the team BABIP is due to the pitchers, but it’s a leap of logic to say that you’re looking at pitching SKILL there. And HITf/x data indicates in fact that you are not.
Also, I don’t understand why you insist on looking at single-season pitcher/team BABIP to determine that number. It is simpler to calculate, but it’s deceptive. Being rooted to single-season numbers is one of the big failings of modern sabermetrics.
Thanks, Matt. Not sure I get how FIP measures the impact of a strikeout directly; how is that model capable of teasing out the different effects? It seems like with less info (only k, bb/hbp, and hr per inning), you’d be relying even more on the peripheral effects K has. Or is that why FIP is not as good of a predictor as SIERA?
thanks again!
Which of my conclusions about the game of baseball do you dispute?
You found that how hard a ball is hit is highly correlated. This is a self-contained statistic that is only useful inasmuch as it can teach you about singles, doubles, triples, home runs, outs, and errors. It doesn’t do me any good to know the statistic otherwise, except for how it relates to outcomes that affect games. So BABIP is a logical skill to try to infer from how hard a ball is hit, and your numbers do a nice job of hitting on that.
I think when you say “half of BABIP was due to how hard the ball was hit,” you’re either using same year data or R instead of R^2 or doing both. I’m guessing you’re doing correlations, while I’m doing R^2.
But if it’s just same year data, you’re including luck in terms of how hard a ball was hit (of course pitchers will deviate around their true talent rate in this category as well). That doesn’t measure skill. That measures outcomes.
My regressions are not intended to be the end-all summary of a pitcher’s true BABIP skill. They pick up about 80% of the possible variance that could exist in BABIP skills.
Since this seems to be a point of contention—how much variance in true BABIP skill there is to find—I’ll prove to you that R=0.5 or even R^2=.25 is insane for one season of data.
Take all pitchers with 150 IP or more in a single season from 2003-2011. They average 592 BIP. There true BABIP skill is about .30, give or take, so the variance in luck HAS to be .21/592 for the average pitcher in this group. It’s impossible binomially for that not to be true. That’s a random variance if .000354. The actual variance in BABIP for that same group is .000457. That means randomness HAS to explain 77% (last time I got 75% but same diff)! I don’t know how much you think is team defense, but you’re it’s not 0%. If you look at how much variance is explainable by defense seriously, it’s about 13%. That’s just regressing the data.
So my original 12% number is the maximum explainable by differences between pitchers. That’s not what my regressioun found. That was 10.4%. Obviously give or take here or there, but you get the point. Most of it is explained by peripherals.
And just because you’re saying I’m looking at single-season numbers to prove that point, that has nothing to do with the implications of that 12%. The 12% means the standard deviation is pitcher skill is about .007 of BABIP. It can’t be much greater than that, and it has nothing to do with choosing a single season. The same analysis on careers or half seasons or whatever would give you about the same conclusion. I look at single-season because it’s the easiest to run these tests on quickly.
So what exactly do you think are my wrong conclusions? Where in that description of variance will you determine that BABIP skill level has a higher spread than about .007, and where as about .005 or .006 can be explained by a regression on peripherals, tell me what’s wrong here. If you want to say there is value in the last .001 or .002, great, keep at it. It may only be attainable with propietary data, and good for you if you can use it to your advantage. But nothing that I have found here is wrong.
Nate:
The way that the individual effect of a strikeout can be determined is by looking at win expectancy matricies. At insidethebook.com, they have all that determined out. It’s Markov marticies and stuff, kind of complicated, but rigorous.
The reason that FIP is worse at predicting ERA than SIERA is largely the K% correlation, yes. Add in the fact that SIERA regresses HR/FB, and that explains some of the benefit of SIERA in RMSE but not in correlation. That SIERA predicts low BABIPs for very-high-GB% pitchers also helps a LOT too. The K/BABIP correlation is a big part of it, though.
So FIP was built off the Markov matrices (giving out a sort of average K-event value) whereas SIERA is a regression of K/PA’s relationship with ERA. Cool, got it.
TB’s low 2011 BABIP is strongly impacted by Hellickson’s ridiculously low .224 BABIP. He accounted for 13% of TB ‘s total IP.
Matt, are you sure about the K value in FIP? I thought Tango had stated that the K value in FIP is not just based on markov chains, but perhaps I’m misunderstanding what you or he have said.
Dave, I might be mistaken. I had remembered it as Markov matricies, but there might be something else there. In general, I think it’s a way of getting the direct effect of a K, but I forget exactly what the procedure entailed.