Foundations of the Dollars-per-WAR Evaluation Framework

It is difficult to replicate production from a star like Robinson Cano with multiple players (via Keith Allison).
When I was younger, I used to love to listen to pitchers talk about how they would grip various pitches. The concept that if I just put my fingers on the perfect spot of the ball, I could snap the perfect curveball appealed to me, but I never really got the ball to spin the right way.
Learning how to play baseball is something that will never be possible on web sites such as this, because you need to learn that on the field. The Moneyball revolution—and the book itself—is fundamentally about how outsiders can improve a team, specifically through team-building in the front office.
Most sabermetric analysis falls into one of these two categories: improving the evaluation of player talent or improving the valuation of player talent. Evaluation entails predicting how players will perform or attempting to strip circumstance from performance to get at a true performance or talent level. Valuation is about how to measure that performance itself.
There are two levels of the “valuation” category—translating the performance into wins and losses (often through a WAR model) and translating those wins and losses into dollars to evaluate transactions. Therefore, at the core of what web sites like this provide is quantifying the impact of transactions that front offices make, and that leads right into the debate over the “Dollars-per-WAR” evaluation framework.
This article will run through several important concepts relating to this topic. My next article will dive into the actual calculations. In this piece, I will:
- Explicitly state the goals of the dollars-per-WAR framework
- Relate this to how teams make personnel decisions and explain why the correct approach is a constant number of dollars per WAR
- Talk about what determines the financial value of a player to a team
- Discuss the impact of variation across teams in these expected financial values
- Explain how the peculiar upward-sloping demand curve for wins combined with a limited supply of free agents creates high salaries
The Goals of Developing a Dollars-per-WAR Framework
The baseball analysis community has both rallied around and rallied against our most common quantitative framework for evaluating free agent contracts, the application of a simple “dollars-per-WAR” model. The model has been debated for years, with competing estimates of value and challenges to the framework itself.
All models are wrong. Any full model that incorporates every aspect of the world is useless—because it would be an exact replica … which, of course, would then need to be modeled itself. When building a model, we make simplifying assumptions to make analysis more tractable, and since those simplifying assumptions are (by definition) wrong, we need to think about what our simplified model misses.
That means we need to define the goals of using a “dollars-per-WAR” framework in advance, which is what this article will do. My next article will actually show the methodology and calculations, so if you’re looking to use that framework to evaluate free-agent signings, that will have to wait until next time. But if you want to make sure you’re applying the analysis correctly, you will need to grasp this piece, as well.
The primary goal of developing a dollars-per-WAR estimate is comparison. The only relevance that a calculated number can have is to see how one deal compares to another. Of course, it is even more useful if we can evaluate one deal compared to all others, which is why the Dollars-per-WAR model is intended to represent the average cost of WAR on the free-agent market. This is our first definition:
Dollars per WAR: The average cost of acquiring one win above replacement on the free-agent market
Comparing the cost per WAR of a single free-agent signing to the average cost is not an automatic up-or-down vote on the transaction itself. In fact, many bad decisions do well according to this test, and many good decisions do poorly. A good move should be evaluated based on the alternatives available, and this requires a judgment call. What criteria should be used to make these judgments is not as black and white as the dollars-per-WAR framework would suggest.
As Russell Carleton astutely pointed out in this article, there should be at least several criteria to evaluating a move (he lists a few), but most importantly considering the actual effect on the win column of a single team (rather than relative to the performance of an imaginary replacement-level player) and the actual effect on the team’s finances, as well.
Several of the criteria Russell mentions in his article relate to GMs who rationally sign players for more than the market average of dollars per WAR. In these cases, an individual player may be the only available player available at a certain position, or the team may have a hole that absolutely needs to be filled. However, I would consider a GM successful if he rarely puts himself in the position of needing to overspend.
I have written several articles about reasons some players tend to cost high or low dollars per WAR. For instance, I’ve written at FanGraphs about how outfielders, relievers and first basemen tend to be expensive, while other infielders and catchers tend to be good bargains. Whether this has a basis in a rational market or not, GMs who carefully maintain a flow of relievers and outfielders in-house to avoid needing to use free agency to acquire these players are making good decisions and should be credited for this.
How Teams Make Personnel Decisions: Budgets or Investments?
The financial aspect of valuation requires an analysis of what determines a team’s spending decisions. Most analysis that is done online assumes a team decides it can afford a certain budget, but that budget is treated as exogenous.
That is how households often make decisions. They have a sense of how much they plan to spend each month and try to make decisions that reflect the best use of these available dollars towards their goals. When households spend money, they do so because pictures of ex-presidents don’t give you direct value but can be exchanged to buy things they do want.
Businesses in the real world purchase things as a means, not an end. I buy a sandwich because I want to eat it—the sandwich is the end goal. The sandwich shop owner buys a bread slicer because this outlay allows him to make more money in the future by selling more sandwiches—the bread slicer is a means to an end. He spends money on employees with the same goal in mind.
Businesses spend money on labor with the idea that the employees will bring in more money than they cost. Budgets for households are set to avoid spending more than they have; for firms, “budgets” are flexible if increasing budgets will increase revenue by a larger sum.
Well, at least all of that is true in the economic models I studied. And as I told you at the beginning of this article, all models are wrong. Owning a baseball team is often lucrative, but it fails the assumptions of the rational market model that economists use as a baseline. Some team owners really do come up with budgets that they deem “affordable” and view the goals of wins added as the ends themselves, while other owners determine the budgets they give to general managers based on a rational investment framework that see wins added as means towards the end of revenue added later.
The reason the canonic economic model here fails is that major league baseball team owners do not get driven out of business (in econ jargon, there is no “free entry”), so running a team foolishly will not lead to a more rational investor stealing your customers. There are 30 teams, and they are set in stone.
However, this fact by itself does not necessarily allow for irrational teams. Even if a current team owner plans to run a team according to a certain set of irrational rules that will lead to a certain profit level, a more intelligent team of investors might determine they could be more profitable and buy the team for even more money. The incumbent owner would notice that his profits will not be enough to turn down the larger offer from the rational investors and would sell to them instead.
The reason that does not happen is that owning a baseball team provides some consumption value itself. It may be that Mike Ilitch’s business plan does not lead to as much profit as that of a potential buyer of the Tigers, but the fact that he enjoys owning the team and wants to consume a World Series championship affects his reservation price and keeps potentially more rational investors from being willing to buy him out.
Fortunately for this article, the “irrational budget” approach and the “rational investor” approach both favor using a dollars-per-WAR framework as a useful tool in evaluating free agent signings. In the event of an owner setting a budget based on some alternative criteria rooted in affordability, getting the most wins out of a fixed set of dollars allotted in a budget is a goal that requires spending the fewest dollars per win added (or more intuitively, getting the most wins per dollar spent).
In the event of a rational investor owner, his goals still will entail adding the most wins possible for a given budget decision. The rational investor owner will just take the extra step of setting that budget based on what level of investment in labor will maximize his profit.
Linearity of the Dollars per WAR Model
The skeptical reader is not and should not be convinced yet that the dollars-per-WAR framework is useful, because I have still left out one step. Although a GM should be trying to maximize the total number of wins he can purchase given his budget, a team is made of 25 players. As Russell Carleton put it in his article, “Free agents are not sold in grocery stores.”
In econ jargon, Russell is making the valid point that this is not a “thick” labor market. It is not difficult to find cashiers for your store once you figure out how many cashiers you want to hire at their current wage levels.
But there may not be a way for the Seattle Mariners to improve equally by acquiring three mediocre players rather than adding Robinson Cano. Even if they are willing to spend $8 million per year on three different mediocre players, they may not be able to find three positions at which they can upgrade from a replacement-level player and three matching free agents who play those positions.
The fact that teams cannot buy “divisible” labor, even if their dollars are divisible, is an important challenge to modeling a linear Dollars-per-WAR cost. However, when I have tried to research this topic, I have always found that there are usually divisible-labor options that make the free agent market “thick” enough.
In this article, I looked at the big-name free-agent signings of the 2009-10 market and found ample opportunities to take the divisible-labor approach to signing multiple non-superstars instead of one superstar. Maybe more recently, the 2013 World Series Champion Red Sox front office employed the divisible-labor approach during the 2012-13 offseason.
The divisible labor approach is possible because nearly every team has enough openings to take this approach instead of spending big money on a superstar. There are ways to upgrade in small parts.
Sure, not every offseason yields a free-agent market with a shortstop and a catcher to the team with only replacement-level in-house options at those two positions. But nearly all teams have replacement-level players who could be supplanted at the back of their rotations, in their bullpens, and often in their outfields. And there are often many options on the free-agent market that could fill these holes. The possibility of trades opens other doors to a many-small-upgrades approach, too.
Once you introduce the possibility of signing multiple players to fill several holes, then spending the equivalent money of a Robinson Cano contract on a set of players becomes an option, which drives his salary down to the sum of his potential alternatives. That gives rise to the linear dollar-per-WAR framework in which teams won’t pay more than three times the price of a 2-WAR player to get a 6-WAR player.
I tested this (using FanGraphs’ old estimate of replacement level) in this article and found that players were indeed paid pretty similarly on a Dollar-per-WAR basis across the talent spectrum. So theory is mirrored by reality, anyway.
Using an appropriate replacement level as the basis for using a linear Dollars-per-WAR framework is important. During the era when Nate Silver was writing at Baseball Prospectus, they used a very low estimate of replacement level. As a result, he estimated that the dollar-per-win curve should be getting steeper as wins increase.
Of course, this was entirely based on the very low replacement level. Since many readily available cheap players were estimated as being worth about 1.0 WARP yet were being paid near the league minimum since they were fungible (replacement level), it looked like cheap players were going for very low dollars per WARP, and that the model wasn’t linear.
But if you look at the red line I have drawn on top of his diagram to reflect a higher replacement level (this becomes the new y-axis), a linear model fits his data quite well, as I’ve shown in red, as well.
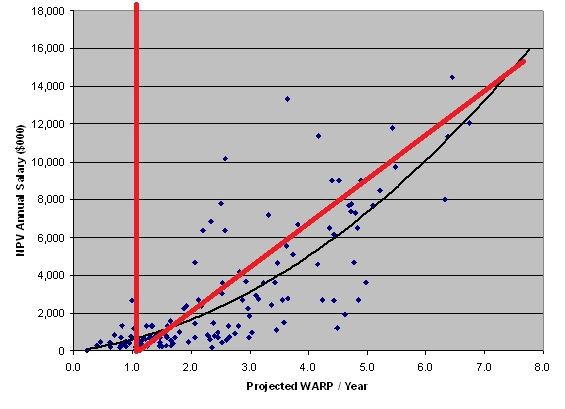
J.C. Bradbury also has made use of non-linear player valuation models, but he does not use replacement level at all. That does not mean he is necessarily using a useless model—remember that all models are wrong, and the simplifying assumptions of any one help you answer different questions, but restrict you from answering others.
In my opinion, the dollars-per-WAR framework provides a nice way of evaluating opportunity cost that I think is useful and transparent enough for much of sabermetric analysis of contracts, even if other methods can help answer questions as well.
Regardless, the dangers of suppressing the constant term (i.e. setting b = 0 in Value = a*WAR + b), which Bradbury cautions against in the linked article, show the importance of picking an accurate replacement level. My previous article linked above suggests the current estimates of replacement level (as well as my own analysis of replacement level directly) are appropriate enough to render the constant-free model useful.
Financial Impact of a Player
The two components of putting a financial value on a baseball player’s labor are evaluating the number of wins that player adds to a team and evaluating the revenue generated by those wins.
The wins the player adds are approximated by the estimated value of WAR you expect from him, as explained in the discussion of linearity above, but Russell’s article also points out the importance of considering variance in that framework, too.
While I certainly agree that depending on whether a team is above or below a 50 percent chance of making the playoffs, it may prefer less or more variance in expected performance, I’m not sure we can pinpoint the variance in WAR of an individual signing well enough yet to really make that a big part of analysis.
Further, I’m not sure that we know yet whether adding two 3-WAR players or a 6-WAR player and a zero-WAR player will necessarily lead to higher or lower variance anyway.
The financial value of wins is going to vary significantly across teams. That does not mean that teams are going to spend different amounts per WAR in the free-agent marketplace, because they still have to bid against each other.
The reality is that the team that actually signs any player has to outbid the Yankees, so they all pay the Yankees’ price. They just buy fewer wins than the Yankees. Instead, let’s talk about all the factors that come into play when estimating the impact of more wins on a given team.
There are several determinants of revenue for major league teams, but the largest sources by far are ticket sales (including playoff tickets) and local television revenue. Remember that teams are not all spending based on some “affordability” determined budget like households, as I described above. Many spend as an investment on baseball player labor, and therefore, we need to invoke the concept of marginal revenue of labor.
This means that players are priced based on the impact that they have on revenue, and the biggest such impact that extra wins have is on ticket sales and playoff ticket sales (both in the present and in the future). As Vince Gennaro documented in Diamond Dollars, a significant share of the value from players comes from making the playoffs, which creates demand for season tickets in subsequent seasons.
Therefore, one of the biggest determinants of how financially valuable a win is to a team is where they are on the “win curve.” The win curve, as explained well by Silver here, reflects the probability of making the playoffs for each given win level:

Of course, the extra step to take is to consider the concept of expected wins when a player is signed versus when he is not and compare those, and in reality you would want to consider the financial implications and probability of each win level to truly evaluate the impact.
However, the conclusion will be the same qualitatively: teams that are closer to the steep part of the win curve are the ones with the biggest potential financial impact of adding a free agent, all else the same, and likely the ones with the highest value for that player.
Team Variation in Financial Value of a Player
Does this mean that teams on the steep part of the win curve should be outspending the dollars-per-WAR league average regularly? No. Keep in mind that baseball player salaries are derived in an auction format. Only one team gets to sign Robinson Cano, and it’s the team with the highest estimate of his financial value to it that should be expected to win that auction.
If you look at the share of free-agent dollars spent by teams on the cusp of the win curve, it is disproportionately high. You see that teams in similarly sized markets will set very different budgets, and those budgets will vary with their place on the expected win curve.
Not only does a team’s place on the expected win curve matter, but the financial impact of those wins can vary greatly, too. Gennaro highlights how different teams have different financial impacts of those wins in this article, and he shows how the Yankees’ marginal revenue of a win is higher than the Braves’ (i.e. the slope representing the change in revenue per win is steeper).
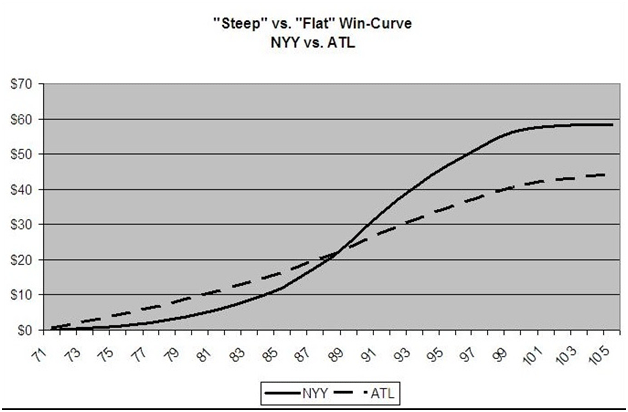
The implications should be clear. If you want your team to spend money, you should hope not only for a large market, but to some extent for a market with sensitive demand. Not only do the Yankees play in a wealthy market, they play in a market with another baseball team–and five other major professional sports teams–as well as countless other entertainment venues. Missing the playoffs is expensive, so the Yankees’ financial value of wins is very high as a result.
Teams also vary in their estimates of how many WAR a player will generate. In fact, the team that signs a player, all else equal, is likely one of the teams with the highest estimate of his talent level. We never know exactly how well a player will play, so teams will differ in their estimates of both WAR and financial value per WAR. Teams with higher values in either or both metrics are more likely to keep bidding until they win the auction.
This is called The Winner’s Curse, and it is commonly cited in sabermetrics as a reason that free-agent salaries are so high. However, this is not an accurate conclusion based on the winner’s curse. Bidders in such an auction know that they are bidding in this environment, and they know that if they win an auction, they likely had a higher estimate of the value than other bidders.
However, the rational approach to this in auction theory is to shade down your bid to reflect the fact that you are likely overestimating the value if you win. Since everyone will shade down bids accordingly, the winner of the auction is still likely to be overestimating the value, but his bid will account for this.
Maybe teams are necessarily this rational in their bidding, but teams undoubtedly do look for red flags if they see other teams dropping out of the bidding. The Winner’s Curse doesn’t explain the high cost of wins in the free-agent market. That has to do with the shape of the win curve and limited supply of free agents available.
Limited Labor Supply and Baseball’s Unique Labor Market
One common mistake people make when looking at dollars-per-WAR estimates is to observe that the average team has about 33 wins above replacement on its roster and that, if each win cost $7 million (per Lewie Pollis), that would supposedly amount to the total value of wins being $231 million. Since 28 teams would certainly lose money at a $231 million payroll, some people conclude that the $7 million per WAR estimates must be too high.
However, this mistakes the average revenue per WAR with the marginal revenue per WAR. The average revenue per WAR reflects the fact that going from 48 wins up to 85 wins provides low revenue products, while wins above the 85-win mark have substantial impacts.
However, when you sum up the revenue of a 93-win team and divide it by the 45 WAR it takes to get there, you’re averaging in the wins between 48 and 85, which were not the valuable ones. The value of most of the wins was low, but the ones they actually bought on the free-agent market were high value. The market price is the marginal revenue, not average revenue, and baseball wins have an upward-sloping demand curve.
This is where baseball’s unique labor market comes into play. If every player were a free agent every offseason, the dollars per WAR spent undoubtedly would come down. But since players need to wait until they have six years of service time to reach free agency, 70 percent of the league’s total WAR is cost controlled. That means that the average team has about 23 cost-controlled WAR, which puts it at about 71-91 if it eschews all players with six years of service time.
Of course, this number is just an average. Some teams have enough cost-controlled talent on their roster that they already have 80-85 wins in store without spending on free agents (see the linked article in the previous paragraph). Giving them all that cost-controlled WAR actually increases their value for non-cost-controlled WAR on free agency.
How much cost-controlled WAR a team has at any given time affects whether it is likely to spend on free agents, but the fact that there are always a few teams on the steep part of the win curve as a result of cost-controlled talent drives the bidding up for free agents among those teams.
Conclusions and Next Steps
A lot of factors go into evaluating how to model free-agent values, and certainly the dollars-per-WAR framework is not the whole story. However, the model has significant value in not only estimating the efficiency of allocated dollars, but also in evaluating how well general managers avoid putting themselves in positions that require overspending. There are a number of caveats cited above, but there are also a lot of false caveats I hope I have debunked.
Now that we know what a dollars-per-WAR framework can and can not do, my next article will show how I calculated values using this model and will compare them to other estimates. I will also revisit some of my prior analysis about variations in dollars per WAR for different types of players and how that applies to smart front-office decision-making.

Great stuff, Matt.
The long term FA megadeal simply uses the last couple of years to subsidize the first couple of years. This gives a false appearance of linearity of $/WAR when viewed narrowly as a current season at AAV.
At any given time, there are guys at the beginning of megadeals and guys at the end. I average them both, and when I do, I get the same cost per WAR as shorter deals. Your comment would only make sense if I restricted myself to looking at the first year of deals. If you only look at the first year, megadeals always look cheap on average!
Exactly – the reason the first year looks cheap is because it is subsidized by backloading. How much would Cano have gotten paid on a one or two year FA deal? We’ll never know – and that skews the entire model toward linearity.
No, it doesn’t. Because A-Rod, Teixeira, Soriano and others are on the tail ends of their deals at the same time. They are getting higher $/WAR just as Cano is getting lower $/WAR. I average them all in. Cano’s projected to get 5 WAR this year so he’s projected to get less than $5MM/WAR, way less than the average. Others like Teixeira and Soriano will get higher than the average. It washes out.
Matt is correct. I have a more elaborate method that basically presumes that a player will generate fewer wins each year and is being paid proportionate to that, and you get the same result.
Well done you.
Great summary article. It intuitively makes sense that adding two 3-WAR players would reduce the variance compared to signing a single 6-WAR guy. Might be interesting to take a look at how this effect plays out, esp. when incorporating the latter part of contracts (assuming those 3-WAR guys have shorter contracts/generally more interchangeable).
Not sure that win curve for the Yankees is accurate. Read in the WSJ that the Yankees lost 50 million in revenue by winning only 86 wins and missing out on the playoffs last year. That curve suggests only a 50 million difference between 71-97 Wins.
“For instance, I’ve written at FanGraphs about how outfielders, relievers and first basemen tend to be expensive, while other infielders and catchers tend to be good bargains.”
Could this be that teams don’t agree with the positional adjustments that are the basis for a large part of a players WAR, and value offense (and power) more so than defense (which is probably in greater supply)?.
The graph with the Yankees win curve is old. I also wouldn’t be surprise if the difference was greater than $50MM now for 71 vs. 97 wins.
If you look through my research on positional differences, I also looked at just comparing players based on offensive value. For your claim to be true, there would not just need to be a difference between how teams value offense versus defense, but a systematic overestimation of the difference in between how well a player would play defensively at one position versus another. That’s possible, but I don’t think it’s true. I would think it’s more likely that outfielders, relievers, etc., are more likely to be swept up in bidding wars since everyone could use a good one, while catchers and shortstops are less likely to benefit from bidding wars because few big spenders have needs at those positions in any given offseason.
hey guys I need your help this is my team is 5 sp and 2 rp max wanted to know where would i need some help this is points league and should I DROP BRAD MILLER FOR KOLTEN WONG BACK UP 2B ANY OTHER IDEAS LOOKING AT MY TEAM :
C Yan Gomes, Cle C
1B Joey Votto, Cin 1B
2B Kelly Johnson, ny 2B
3B Manny Machado, Bal 3B
SS Everth Cabrera, SD SS
OF Ryan Braun, Mil OF
OF Jose Bautista, Tor OF
OF Matt Holliday, StL OF
UTIL David Ortiz, Bos DH
Bench Billy Hamilton, Cin OF
Bench Torii Hunter, Det OF
Bench mike moustakas,kc 3B
Bench brad miller, sea ss
sp Madison Bumgarner, SF
sp Chris Sale, CWS
sp Alex Cobb, TB
sp Julio Teheran, Atl
sp Alex Wood, Atl
rp Ernesto Frieri, LAA
rp Aroldis Chapman, Cin
Batting
Singles (1B) 1 Doubles (2B) 2
Triples (3B) 3 Home Runs (HR) 4
Walks (BB) 1 Runs Scored (R) 1
Runs Batted In (RBI) 1 Stolen Bases (SB) 2
Strikeouts (K) -0.5 Hit by Pitch (HBP) 1
Caught Stealing (CS) -1
Pitching
Innings Pitched (IP) 1.5 Earned Runs (ER) -1
Wins (W) 5 Losses (L) -5
Saves (SV) 5 Blown Saves (BS) -3
Strikeouts (K) 1 Hits Allowed (H) -1
Walks Issued (BB) -1 Hit Batsmen (HB) -1
Quality Starts (QS) 3